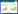文章信息
- 马智雄, 廖锐全, 杨汉杰, 时国伟, 王智慧, 张兴凯
- MA Zhixiong, LIAO Ruiquan, YANG Hanjie, SHI Guowei, WANG Zhihui, ZHANG Xingkai
- 黏度对管内螺旋流径向压差的影响规律研究
- Study on the influence of viscosity on radial pressure difference of spiral flow in pipe
- 中国测试, 2024, 50(5): 36-41
- CHINA MEASUREMENT & TEST, 2024, 50(5): 36-41
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022110052
-
文章历史
- 收稿日期: 2022-11-09
- 收到修改稿日期: 2023-01-09
2. 中国石油天然气集团公司气举试验基地多相流研究室,湖北 武汉 430100;
3. 油气钻采工程湖北省重点实验室,湖北 武汉 430100;
4. 中国石油天然气股份有限公司西南油气田分公司蜀南气矿,四川 泸州 646000;
5. 青海中油甘河工业园区燃气有限公司,青海 西宁 810099
2. Laboratory of Multiphase Pipe Flow of Gas Lift Test Base of CNPC, Wuhan 430100, China;
3. Key Laboratory of Drilling and Production Engineering for Oil and Gas, Hubei Province, Wuhan 430100, China;
4. Shunan Gas Mine, Southwest Oil and Gas Field Branch, PetroChina Company Limited, Luzhou 646000, China;
5. Qinghai Zhongyou Ganhe Industrial Park Gas Co., Ltd., Xining, 810099, China
油井产量计量是油田生产管理中的一项重要工作,及时准确的油井产量资料是跟踪油藏区块动态、预测区块开发潜力、合理制定生产方案的重要依据[1]。由于稠油自身物性的特殊性,产量准确计量非常困难。研发稳定安全、准确度高的稠油计量技术十分必要。
我国油水两相流测量技术的研究从20世纪80年代末期开始,近年来,有了快速发展。马龙博[2]通过将文丘里管与Coriolis流量计相结合进行油水两相流测量,由于文丘里管流量测量的需要,同时提出一种油水两相流流型识别新方法。Shi等[3]研制了一种利用油水密度差异性的静态起旋器,当有油水两相流流体通过时,离心力会将油相和水相分别甩向管道轴心处以及贴近管内壁的区域,管道内形成一种油相在内、水相在外的强制环状流状态,这使得油水分离变得简单,但分离效果不好,不能满足油水两相流含水率的测量。李琦瑰等[4]通过采用文丘里管作为节流装置,利用差压法原理实现了油水两相流流量测量,并进行了相应实验研究验证,但是文丘里管与混合密度计组合时精度尚可,与体积流量计组合时测量精度不够。王帅等[5]在管内相分隔技术产生的径向压差在单相流测量基础上,系统研究了基于管内相分隔产生的径向压差在多相流测量的理论机理,并进行了实验验证。在此基础上,刘明[6]研制了一款先经过旋流器除气、整型,再由电磁流量计进行测量的装置,并通过了大量实验来验证。王帅等[7]提出基于管内相分隔技术可以在管道横截面产生径向压差和沿管道壁面变化的轴向压差,并通过研究发现两种压差与油水两相流的总流量和相含率有一定函数关系,通过利用这一特性可以实现油水两相流中的含水率测量。Yang等[8]针对具有较高含水率的油水两相流提出了一种将电磁流量计和相分隔方法相互结合的含水率测量新方法。相分隔的运用为电磁流量计排除了不导电相散乱分布的影响,使其测量环境得到改善。Wang等[9]采用管内相分隔法建立了油水两相流中沿管道轴线方向和某横截面沿半径方向的两个压力差的耦合模型,并通过现场实验数据验证了该测量模型的可行性。虽然国内外学者在油水两相测量技术取得了一定进展。但是研究主要集中在结构优化,内部流场数值模拟等。对于油水两相测量中油相黏度对径向压差的影响研究较少[10]。
在实验室条件下难以使用超稠油进行实验,对黏度数值划分也不够准确,通过数值模拟的方法更为方便准确。因此,本文为探索研究油相黏度对管内油水两相螺旋流径向压差的影响规律,通过数值模拟的方法对研究设计的测量装置内部流场的油水相分布规律,速度场和压力变化规律进行研究,为油水两相流测量装置的结构设计和改进提供思路。
1 管内油水两相流量测量机理 1.1 测量结构经研究设计油水两相流测量装置如图1所示,静态被动起旋装置(旋流器)产生离心力实现螺旋流。前端椭圆部分是为了流体流入旋流器叶片部分时均匀稳定连续进入,这样不会产生紊乱的流体对压差的取值以及模拟数据产生较大影响。叶片均匀环绕在中心圆柱四周。装置径向压差可由下式求得:

|
| 图 1 油水两相流测量装置几何结构 |
| $ \Delta {P_{\text{r}}} = {P_1} - {P_2} $ | (1) |
螺旋流是流场中的一种现象,因其具有较大的涡量和动能,在流动中有重要的作用。在管内油水两相螺旋流研究过程中发现,在理想状态下,当一定速度的油水混合介质由旋流器入口切向进入后,由于油相与水相间的密度差异,油水依靠自身动力流过旋流器后,密度较大的水相由于所受离心力较大,会被甩至管壁周围,而密度较小的油相所受离心力较小,聚结到管道中心。最终形成“油核-水环”的流动,见图1,在径向形成压力差。
径向压差是油水两相流在旋流状态下由于离心力的作用而产生的,在油核中心与壁面之间存在压差。在理想条件下,可以将径向压差看作是由管中心到油水分界面和油水分界面到管壁的压差。
| $ \Delta {P_{\text{r}}}{\text{ = }}\Delta {P_{{\text{ro}}}} + \Delta {P_{{\text{rw}}}} $ | (2) |
式中:
通过研究发现,当单相流体流过时,流量与径向压差间有一定函数关系,如下式所示:
| $ {Q_{\text{d}}} = \alpha \frac{{\pi {D^2}}}{4}\sqrt {\rho \Delta {P_{\text{r}}}} $ | (3) |
其中,
油水两相通过旋流器时,王帅等[5]研究发现流量与径向压差
| $ {Q_{\text{m}}} = \alpha \frac{{\pi {D^2}}}{4}\sqrt {{\rho _{\text{w}}}\Delta {P_{\text{r}}} - C{\rho _{\text{0}}}({\rho _{\text{w}}} - {\rho _{\text{0}}})\sqrt {{\lambda _0}D} } $ | (4) |
式中:
当测量出旋流器下游某截面的径向压差
油水两相流测量装置网格划分示意图如图2所示。

|
| 图 2 测量装置网格划分示意图 |
网格划分的质量直接影响到数值模拟结果的可靠性和计算精度。本文采用Workbench中提供的Meshing模块进行网格划分。由于入口处安装了旋流器结构,采用结构化和非结构化的组合式网格划分的方法,并对旋流器局部进行网格加密,网格划分如图2所示。并使用径向压差对网格数量进行独立性检验,不同网格数条件下的计算结果如图3所示,随着网格数的增加,径向压差先增大后基本保持不变,当网格数大于380000时,径向压差基本不随网格数的增加而变化,为了提高计算精度和计算效率,最终确定最优网格数是380000个。
|
| 图 3 网格无关性验证 |
2.2 计算模型和控制方程
采用Fluent19.0软件进行数值模拟。由于装置内流动涉及离心力的变化,多相流模型选用Mixture模型,与VOF模型和欧拉模型相比,因Mixture模型适用于重力,离心力或其他体积力作用下的液滴计算,并且Mixture允许相间的穿插及相间滑移。湍流模型选用RNG k-ε模型,与k-ε模型相比,RNG k-ε模型在基础之上考虑涡流对湍流的影响,提高了对旋涡流动的计算精度,提高了旋转流动计算时的准确性,RNG k-ε模型更适用于研究黏度对油水两相流测量的影响。装置内的控制方程为连续性方程、质量守恒方程和动量守恒方程[11]。
连续性方程:
| $ \frac{{{\mathrm{d}}\rho }}{{{\mathrm{d}}t}} + \rho \nabla \cdot {{u}} = 0 $ | (5) |
其中,
| $ \frac{{\partial \rho }}{{\partial {{t}}}} + \frac{{\partial (\rho {u_x})}}{{\partial x}}x + \frac{{\partial (\rho {u_y})}}{{\partial x}}y + \frac{{\partial (\rho {u_{\textit{z}}})}}{{\partial {\textit{z}}}}{\textit{z}} = 0 $ | (6) |
如果为不可压缩流动,即密度ρ为常数
| $ \rho \nabla \cdot u = 0 $ | (7) |
动量方程:
| $ \rho \frac{{{\text{d}}u}}{{{\text{d}}t}} = \rho f + \nabla \cdot \sigma $ | (8) |
式中:
边界条件采用速度进口和压力出口,壁面边界条件采用无滑移壁面,其他物性参数根据相应条件设定。研究不同流量10~80 m³/d、不同含水率30%~90%及不同油相黏度下50~15000 mPa·s,管内油水两相流螺旋流径向压差特性变化规律。具体模拟方案如表1所示。
| 油水混合流量/ (m3∙d–1) |
含水率/% | 油相黏度/(mPa·s) |
| 10、20、30、40、 50、60、70、80 |
30、50、70、90 | 50、100、2000、5000、6000、9000、 10000、11000、12000、13000、 14000、15000 |
3 数值模拟结果及分析 3.1 油水相分布规律
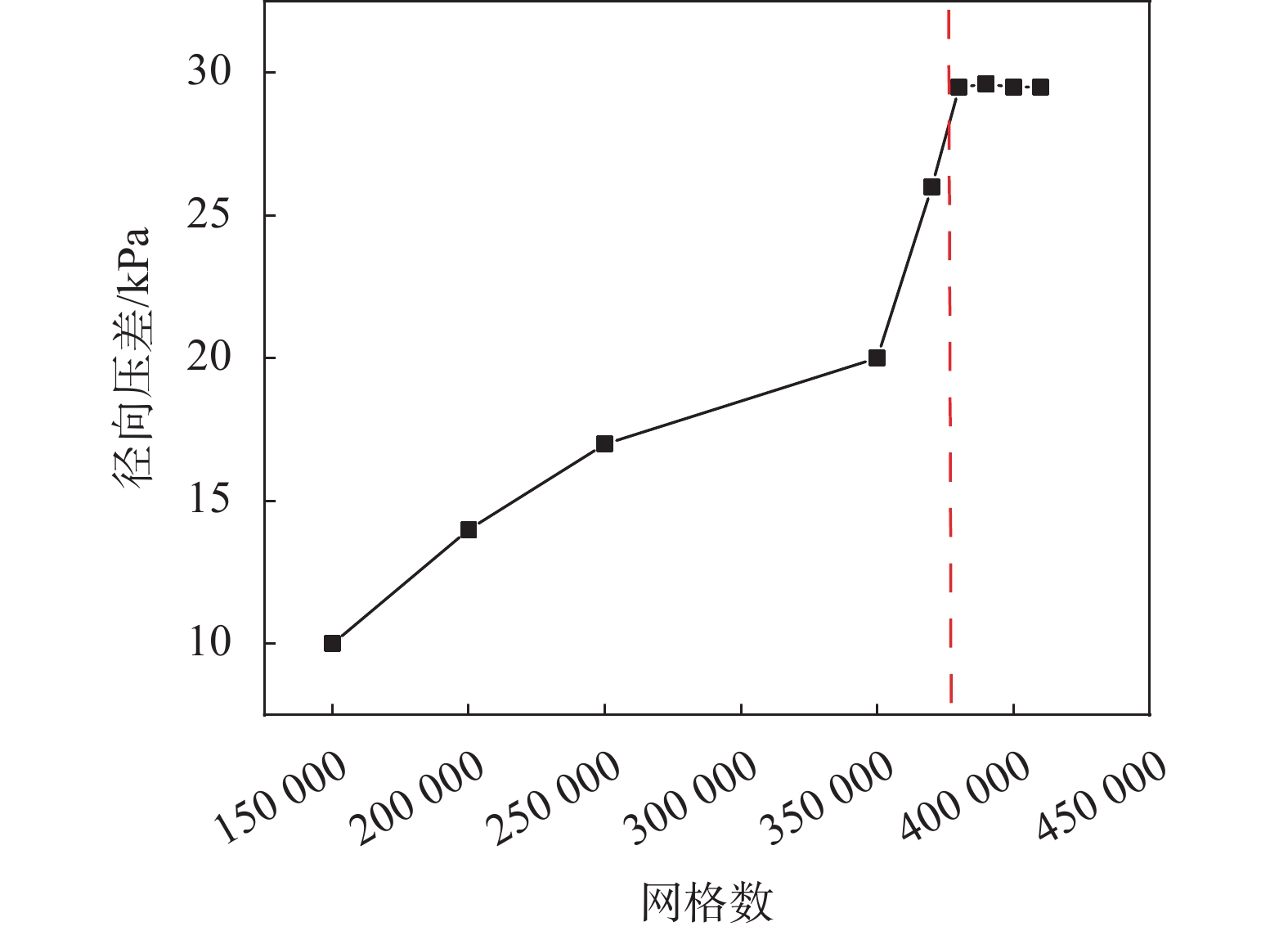
以含水率50%,油水混合流量80 m³/d工况为例。H截面不同黏度水相分布图如图4所示。
|
| 图 4 水相分布云图及速度矢量图 |
由图4可以看出,在保持油水混合表观流速不变,当油相黏度较低时,通过旋流器后油水分界较为明显,形成稳定的“油核+水环”分布。当油相黏度逐渐增大时,油不能被充分分离而形成油块,水环被黏度较大的油块破坏,油水分布混乱。
造成此种现象的主要原因是在随着油相黏度增加时管内的摩擦损失也在不断增加,油滴穿过水相时需要更大能量,致使油滴向管中心迁移难度加大,管中心的油滴数量会减少。所以,随着油相黏度增加,管中心的油相分布逐渐分散,未形成完整的油核。
3.2 轴向速度分布选取含水率为50%、油水两相流混合流量为80 m3/d的工况进行分析,H截面上轴向速度的分布如图5所示。

|
| 图 5 油相黏度对轴向速度的影响 |
由图5可知,在研究范围内随着油相黏度的增加,轴向速度分布变化规律基本一致,旋流后管道中心速度较低,截面流速分布从管中心到管壁先上升后下降,轴向速度沿着轴向对称,呈 “M”型分布。随着黏度的增加,在同一截面上的流体轴向速度明显下降。当油相黏度从500 mPa·s增加到8000 mPa·s时,轴向速度由其峰值的7.45 m/s降低为4.9 m/s,且当油相黏度超过10000 mPa·s后,轴向速度变化幅度减小。
3.3 径向压差变化规律分析 3.3.1 不同流量、不同含水率下径向压差变化规律选取H截面上不同含水率、不同流量工况下径向压差变化趋势如图6所示。

|
| 图 6 流量、含水率对径向压差的影响 |
由图6可知,当油水混合流量保持一定时,随着含水率的增加,径向压差减小幅度降低。当含水率保持一定时,随着油水混合流量增加,径向压差逐渐增加。随着油水混合流量增加,油水两相流通过旋流器时产生的离心力增大,从而使管壁与管中心的压差增大。由图可以看出径向压差会随着油水混合流量的增加而增加,且具有高度相关性。
3.3.2 不同黏度下径向压差变化规律在装置结构参数不变的情况下,当黏度增加,径向压差
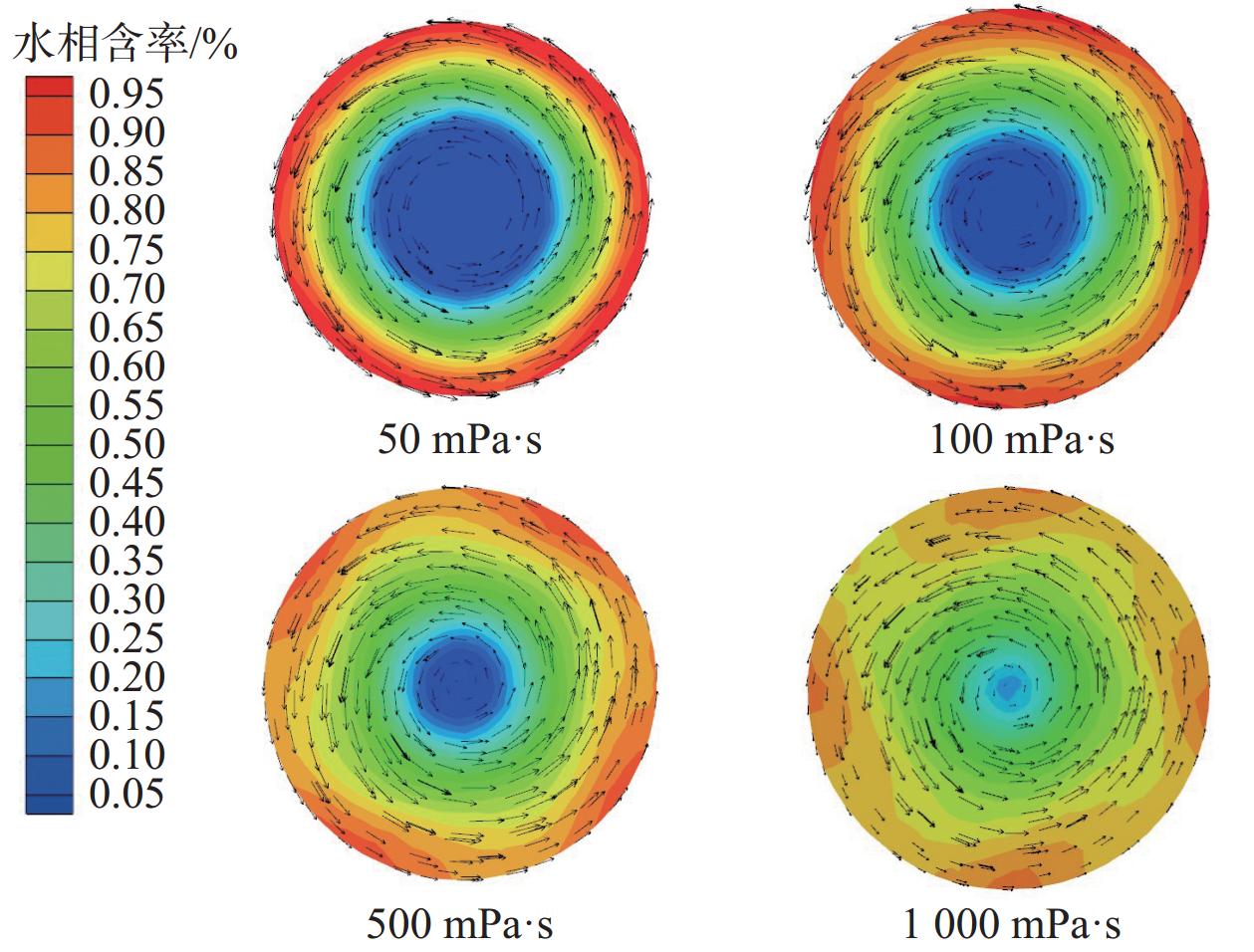
选取旋流器末端的H截面,选取含水率为50%、油水两相流混合流量为80 m³/d的工况进行分析,H截面上径向静压分布如图7所示。旋流器纵截面湍动能分布云图如图8所示。
|
| 图 7 油相黏度对径向静压的影响 |

|
| 图 8 不同油相黏度下湍动能分布云图 |
由图7看出,由于旋流离心力的作用,静压力沿轴向呈明显对称分布,油水两相经过旋流后管道中心压力最小,从管道中心到管壁压力逐渐增加,从而形成径向压差。随着油相黏度的增加,中心到壁面压差变化逐渐减小,不利于油滴向中心运移。同时油滴向管中心运动所受黏性阻力变大,油相与水相间的摩擦力变大,导致管内动能逐渐降低。
由图8看出,湍动能数值随着黏度的增加而增大,且湍动能随黏度变化上升变化较快,流体黏度对管内流速的影响逐渐增大[13]。
选取旋流器末端的H截面,不同含水率下,径向压差与黏度的变化关系如图9所示。
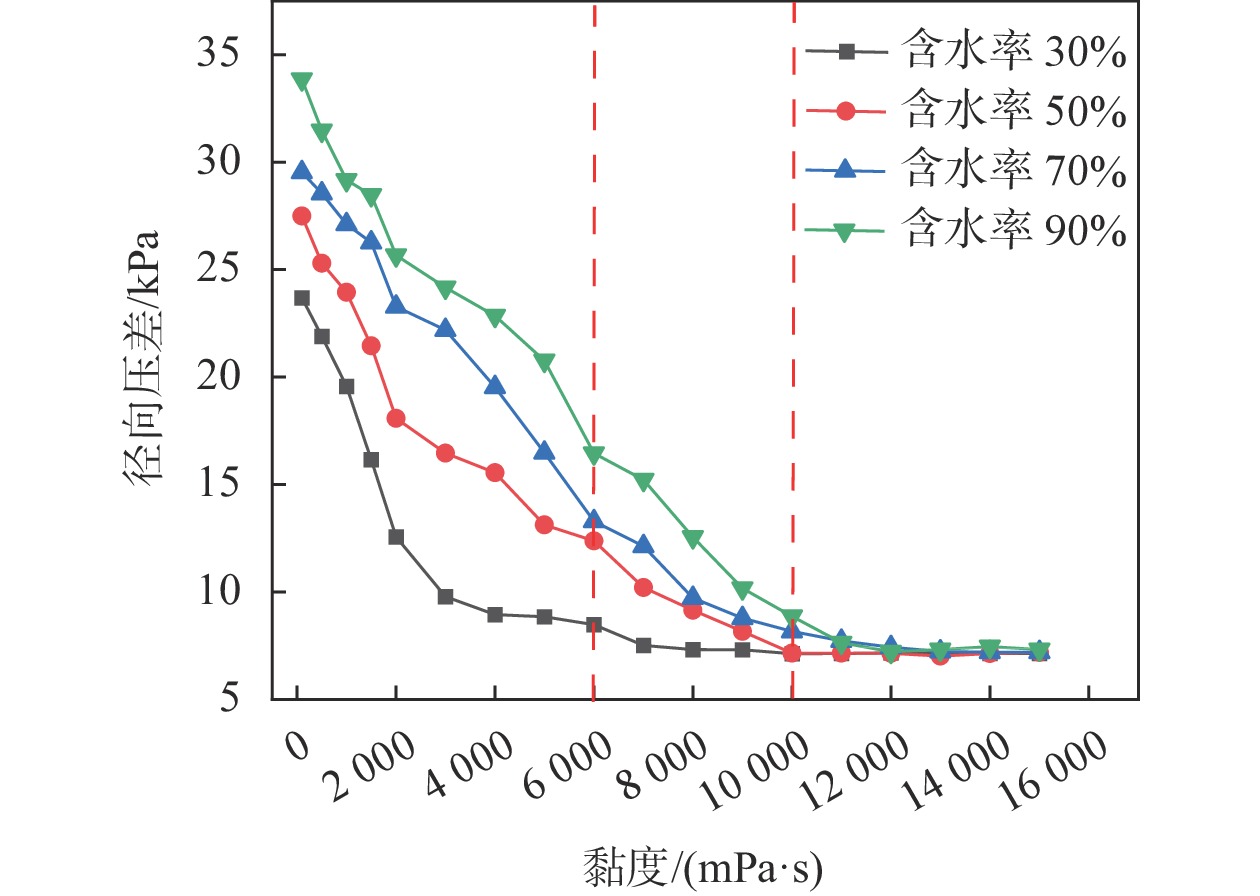
|
| 图 9 油相黏度对径向压差的影响 |
在黏度0~6000 mPa·s时径向压差变化如图9所示,当油水混合流量、含水率保持一定时,径向压差与黏度呈负相关关系,径向压差的值随黏度升高而逐渐减小。
在黏度6000 ~10000 mPa·s变化时,径向压差变化趋势逐渐趋于平缓。在超过10000 mPa·s后,径向压差不再随着黏度的升高而变化,逐渐趋于稳定。此时,径向压差只与流量有关。通过分析可知,随着油相黏度的增加,流体流经旋流器后所受黏性阻力变大,并且油水两相流的湍动能因为黏度的变大而有明显的增加,管内流速明显减小,此时流体获得的向心加速度即离心力在逐渐减小,导致压力梯度不断变小。因此,油水两相流经旋流器后的径向压差不再受油相黏度影响。
由于油水两相流通过装置时的相分布和速度分布总是对称的,流量的测量不受流型限制,王帅等[5]发现径向压差与流量有一定函数关系,利用公式(4)可以实现油水两相流流量测量,经本文研究发现黏度超过10000 mPa·s后,径向压差不再随着黏度的变化而变化,只是流量的单值函数,即径向压差与黏度无关,只取决于油水的混合流量。可以利用此机理,实现油水两相流流量测量。
4 结束语使用计算流体动力学软件Fluent数值模拟方法,通过分析油相黏度对管内油水两相螺旋流的径向压差特性,得出如下结论:
1)油-水两相流在通过旋流后受离心力作用被重整为“油核-水环”的流型。随着黏度的增加,管中心的油相集中度下降较快。
2)在研究范围内,轴向速度与静压力分布规律基本一致。轴向速度和静压力沿着轴向对称分布,随着黏度的增加,在同一截面上轴向速度明显下降。同时中心到壁面的压差逐渐减小。
3)在黏度0~6000 mPa·s时,当油水混合流量, 含水率保持一定时,径向压差与黏度呈负相关关系。在黏度6000 ~10000 mPa·s时,径向压差变化趋势逐渐趋于平缓。在超过10000 mPa·s后,径向压差不再随着黏度的升高而变化。此时,径向压差只与油水混合流量有关。
| [1] |
刘莹莹, 刘楠楠, 李晓平, 等. 油水两相管流测量方法应用进展[J].
油气田地面工程, 2020, 39(2): 10-16.
LIU Y Y, LIU N N, LI X P, et al. Application progress of measurement method for oil-water two-phase pipe flow[J].
Oil-Gasfield Surface Engineering, 2020, 39(2): 10-16.
|
| [2] |
马龙博. 油水两相流量测量研究及在三相流量测量中的应用[D]. 杭州: 浙江大学, 2006.
MA L B. Research on the flow measurement of oil-water two-phase flow and its application to the flow measurement of oil-gas-water three-phase flow[D]. Hangzhou: Zhejiang University, 2006.
|
| [3] |
SHI S Y, XU J Y, SUN H Q, et al. Experimental study of a vane-type pipe separator for oil-water separation[J]. Chemical Engineering Research and Design, 2012, 90(10), 1652-1659.
|
| [4] |
李琦瑰, 杜雪麟. 差压法测量油水两相流流量[J].
石油化工高等学校学报, 2015, 28(1): 70-77.
LI Q G, DU X L. Flow measurement of the oil-water two phase flow by differential pressure method[J].
Journal of Petrochemical Universities, 2015, 28(1): 70-77.
DOI:10.3969/j.issn.1006-396X.2015.01.015 |
| [5] |
王帅, 王栋, 董宝光, 等. 基于管内相分隔的径向压差在多相流测量的应用[J].
化工学报, 2018, 69(12): 5049-5055.
WANG S, WANG D, DONG B G, et al. Radial differential pressure used in multiphase flow metering based on phase-isolation[J].
CIESC Journal, 2018, 69(12): 5049-5055.
|
| [6] |
刘明. 管内相分隔状态下电磁流量计测量气液两相流的方法[J].
石油与天然气化工, 2020, 49(6): 95-100.
LIU M. Gas-liquid two-phase flow measurement by electromagnetic flowmeter under phase-isolation state[J].
Chemical Engineering of Oil and Gas, 2020, 49(6): 95-100.
DOI:10.3969/j.issn.1007-3426.2020.06.016 |
| [7] |
王帅, 李庆芝, 陈建英, 等, 管内相分隔双压差在多相流双参数测量中的应用[J]. 化工学报, 2020, 71(12): 5515-5520.
WANG S, LI Q Z, CHEN J Y, et al. Dual differential pressure used in multiphase flow double-parameter metering based on phase-isolation[J]. CIESC Journal, 2020,71(12): 5515-5520.
|
| [8] |
YANG Y, HA W, ZHANG C, et al. Measurement of high-water-content oil-water two-phase flow by electromagnetic flowmeter and differential pressure based on phase-isolation[J]. Flow Measurement and Instrumentation, 2022, 84: 102142.
|
| [9] |
WANG S, WANG D, ZHANG W, et al. Coupled model of dual differential pressure(DDP) for two-phase flow measurement based on phase-isolatio method[J]. Flow Measurement and Instrumentation, 2021, 80: 102005.
|
| [10] |
刘庆超, 王尊策, 徐艳, 等. 采出液黏度对液-液分离旋流器性能的影响[J].
北京石油化工学院学报, 2019, 27(1): 8-13.
LIU Q C, WANG Z C, XU Y, et al. Effect of viscosity on the performance of liquid-liquid separation cyclone[J].
Journal of Beijing Institute of Petro-chemical Technology, 2019, 27(1): 8-13.
|
| [11] |
林刚, 纪艳娟, 郭鹏, 等. 操作参数对柱形油水分离旋流器性能的影响[J].
石油工业技术监督, 2018, 34(11): 1-4.
DOI:10.3969/j.issn.1004-1346.2018.11.001 |
| [12] |
杨琳, 梁政, 田家林, 等. 粘度对液-液旋流器内部流场及分离效率影响的仿真分析[J].
流体机械, 2010, 38(3): 28-32.
YANG L, LIANG Z, TIAN J L, et al. Simulation study on viscosity impacting on the internal flow field and separation efficiency of liquid -liquid cyclone[J].
Fluid Machinery, 2010, 38(3): 28-32.
|
| [13] |
陈利琼, 李姝璇, 王佳营, 等. 基于正交试验的油水分离器整流构件参数优化[J]. 中国测试, 2023, 49(6): 151-156.
CHEN L Q, LI S X, WANG J Y, et al. Parameter optimization of oil-water separator rectifying component based on orthogonal test[J]. China Measurement & Test, 2023, 49(6): 151-156.
|
 2024, Vol. 50
2024, Vol. 50