0 引　言

在西北、东北等寒冷地区，冻融循环引起混凝土材料性能退化是造成建筑物结构耐久性能衰退的主要原因之一，尤其我国的东北和西北地区，大坝、水渠等水工混凝土结构由于冻融破坏都受到不同程度的影响^[1-2]。混凝土冻融后的典型特征是表面变化和内部损伤，两者变化均与微观孔结构密切相关^[3]。

孔径分布和孔隙率作为微观孔结构的两个重要参数都会对混凝土的力学性能和耐久性能造成直接影响^[4-6]。同时，研究人员对冻融循环过程中混凝土内部孔隙的膨胀规律进行了大量的试验和理论研究。Jacobsen等^[7]利用SEM分析表明，混凝土冻融前1~10 μm孔径较少，0.5~1 μm孔径较多，而冻融后形成的1~10 μm孔径增加；Kumar等^[8]利用MIP研究了不同养护龄期的混凝土抗压强度与孔隙率、孔径分布之间的关系；田威等^[9]和Yuan等^[10]为研究混凝土内部孔隙结构的演化规律采用CT扫描进行三维重构。但以上方法依然存在局限性：例如，电子显微镜法（SEM）要求样品体积小，无法精确表征混凝土整个结构；采用压汞法测试存在冻融循环过程中试件内部与外表面的不一致，以及压汞测试过程中，高压作用下混凝土微孔结构的破坏都降低混凝土孔结构冻融损伤分析结果的可信度。

目前，核磁共振（NMR）技术作为一种新的快速检测岩石、混凝土和其他多孔介质微观结构方法，具有无损、快速、准确的特点，该方法以水为介质，可以用来获取孔隙度、孔径分布和横向弛豫时间分布等参数^[11-12]。然而，通过核磁共振测得的孔隙结构与混凝土冻融循环中的力学性能关系研究较少。此外，目前关于冻融循环过程中混凝土力学性能与孔隙结构之间的数学基础模型并没有深入研究。

基于以上原因，本文以低场核磁共振（NMR）测试不同冻融循环次数下混凝土的微观孔结构等数据，结合冻融循环过程中混凝土力学性能；通过灰色关联熵理论建立不同冻融循环过程中混凝土力学性能与微观孔隙结构参数的数学模型，该研究成果可为寒区水工混凝土结构的耐久性提供一定的理论参考。

1 原材料及试验方法 1.1 原材料

水泥采用P·O 42.5级普通硅酸盐水泥；河砂采用天然河砂，细度模数为2.8；粗骨料采用粒径5~31.5 mm连续级配碎石，压碎指标6.7%；减水剂采用LC-HPC聚羧酸高性能减水剂，减水率25.1%；水采用自来水。

1.2 试验方法

混凝土配合比如表1所示。冻融循环试验依据GB/T 50082—2009《普通混凝土长期性能和耐久性试验方法标准》 ^[13]规范中的快冻法进行，试验过程中对外观现象、动弹性模量以及抗压强度进行测试，总冻融循环次数为200次。孔结构测试采用苏州纽迈分析仪器股份有限公司生产的大孔径核磁共振成像分析仪（MacroMR12-150H-I），测定冻融循环0、50、100、150、200次后的混凝土孔结构特征，试件尺寸为Φ=100 mm，H=50 mm。扫描电子显微镜试验采用Gemini 500进行测试，测试电压为5 kV，试件尺寸为0.5 cm×0.5 cm。

2 结果与讨论 2.1 外观分析

图1所示为混凝土试件冻融循环25、50、75、100、125、150、175、200次后的表观现象。可以看出，从冻融循环0次到200次，棱柱体试件的外表面砂浆脱落、骨料外露的现象变得越来越严重。从冻融循环0次到75次，棱柱体试件外观无明显缺陷；经过冻融循环125次后，试件外表面有碎片剥落以及微小裂隙产生的现象；冻融循环150次后，可以明显观察到混凝土外表面水泥砂浆剥落明显，且伴随着明显的裂隙和孔洞的产生，混凝土试件冻融循环损害明显；冻融循环200次后，表面的水泥砂浆完全剥落，外表面石子裸露，混凝土发生显著的破坏。

2.2 力学性能分析

图2所示为混凝土不同冻融循环后的抗压强度和动弹性模量测试值。结果表明，冻融循环100次时抗压强度损失达到19.3%，动弹性模量损失达到28.4%，而冻融循环200次后抗压强度损失达到56.4%，动弹性模量损失达到61.72%，力学性能指标大幅度下降。因此，当混凝土冻融循环200次后已出现严重的损伤。

2.3 SEM微观分析

图3所示为不同冻融循环次数混凝土SEM图。从图3（a）可以看出，冻融循环0次，混凝土内部结构致密、均匀，水化产物明显且无明显裂纹；如图3（b）~（c）所示，反映了混凝土孔隙水在冻结过程中，在孔隙内产生很大的冻胀力，挤碎了孔隙周围的结构，导致孔隙率逐渐变大，内部开始出现裂缝；如图3（d）所示，冻融循环200次，混凝土内部已出现较多裂缝和孔隙。因此，由于冻融循环会使得混凝土内部孔隙结构变得疏松，且出现更多大而圆的新孔隙，造成孔隙的直径以及数量均有所增加。不同冻融循环次数混凝土SEM分析结果与力学性能、外观表征、孔隙结构变化趋势相吻合。

2.4 孔结构分析

核磁共振试验测试采用CPMG脉冲序列采集数据，测定混凝土横向弛豫时间，通过弛豫时间反映混凝土内部孔隙结构特征。弛豫时间与孔隙结构之间的关系可近似简化为^[14]：

式中：$ {\rho _2} $——多孔介质横向表面弛豫强度(μm·s^–1)，只与试件孔隙表面及胶结物的性质有关；

（S/V）_pore——孔隙比表面积。

2.4.1 $ {T_2} $分布曲线及谱面积

如图4所示为不同冻融循环次数下混凝土核磁共振T₂谱分布图。从图中可知，混凝土T₂谱分布曲线包含3个峰值（峰1、峰2、峰3），从左到右分别为微孔、中孔和大孔。结果表明，随着冻融循环次数的增加，T₂谱弛豫起始时间在右移，同时，信号强度在不断地增大，说明随着冻融循环次数的增加，混凝土内部微小孔隙不断连通形成大孔隙，导致信号强度增加。

计算出不同冻融循环次数下混凝土$ {T_2} $谱面积大小与占比见表2和图5。由表可知，混凝土冻融循环由0次增加到200次，T₂谱总面积从1241.87 ms增加到4999.28 ms；同时，0次冻融循环时，$ {T_2} $谱峰1面积占比最大，达到了81.63%，说明混凝土未冻融时试件内部以微小孔隙为主；从冻融循环0次到200次，第一峰面积占比由81.63%减小到47.38%，第二峰和第三峰面积占比增加，这表明随着冻害的积累，外部水分继续迁移到新产生的孔隙中，产生混凝土的内部冻胀压力和渗透压力增加，孔隙结构继续恶化，小孔隙继续发育、扩大甚至渗透，形成中孔和大孔。

2.4.2 孔径分类

通过计算，结合吴中伟等^[15]将混凝土冻融作用下孔径划分为无害孔（0~0.02 μm）、少害孔（0.02~0.05 μm）、有害孔（0.05~0.2 μm）、多害孔（>0.2 μm)四部分，可以得出不同冻融循环次数下混凝土各区间的孔隙分布如图6所示。由图可知，冻融循环200次的混凝土多害孔比冻融循环0次的混凝土多害孔占比增加了35%，有害孔占比从5%增加到23%，增加了18%；少害孔占比从52%减小到23%，减小了29%；无害孔占比从24%减小到1%，减小了23%，当冻融循环200次后，混凝土内部无害孔占比仅为1%。因此，有害孔和无害孔占比的增加是导致混凝土力学性能衰减的根本原因。

2.4.3 饱和度

以T_2截止值（10 ms）作为自由流体饱和度和束缚流体饱和度的界限值，小于10 ms为束缚流体饱和度，代表水溶液存在于小孔隙中；大于10 ms为自由流体饱和度，代表水溶液存在于大孔隙中^[16]。可以得出，不同冻融循环次数下混凝土饱和度和孔隙度见图7。由图可知，从冻融循环0次到200次，孔隙度呈增长趋势，孔隙度最终由0.31%增加到0.64%；自由流体饱和度随冻融循环次数呈现增长趋势，由18%增加到57%，增加值为39%；束缚流体饱和度随冻融循环次数呈现下降趋势，由82%减少到43%，减小值为39%。

3 基于灰关联熵分析冻融循环后强度模型预测 3.1 灰色关联熵分析

为分析不同冻融循环次数下混凝土孔隙结构对抗压强度的影响程度，采用灰色系统理论进行相关性分析。灰色关联分析能分析和确定各因素之间的影响程度或若干个子因素(子序列)对主因素(母序列)的贡献程度^[17]。能够更加明确区别出具体孔隙结构对冻融循环过程中混凝土力学性能衰减的影响。

以混凝土冻融循环0次，50次，100次，150次以及200次的抗压强度Y={Y(k)|k=1,2$ ,\cdots , $ n}选取为参考序列，将对应不同冻融循环次数下所测的混凝土谱面积、孔隙度、自由流体饱和度、束缚流体饱和度、无害孔占比、少害孔占比、有害孔占比以及多害孔占比X_i={X_i(k)|k=1,2$,\cdots , $ n；i=1,2$,\cdots , $ m}作为比较序列，先将试验所得数据进行均值无量纲处理，如表3所示。后根据式（2）~（4）计算出不同冻融循环次数下混凝土抗压强度（参考序列）与孔隙结构参数和孔隙半径区间占比（比较序列）的灰熵关联度和灰关联熵，如表4所示。

式中：P_h——灰关联系数分布密度值；

H(P_h) ——灰关联熵；

E( X_i )——灰熵关联度；

$ {\xi _i}(k) $——灰关联系数；

H_max——差异信息列的最大熵，H_max=ln n。

由表4可知，按照灰熵关联度对孔结构参数进行排序为：自由流体饱和度>孔隙度>谱面积>束缚流体饱和度；孔隙占比对抗压强度影响程度按灰熵关联度排序为少害孔>多害孔>有害孔>无害孔。由此可得，自由流体饱和度和少害孔对不同冻融循环次数下的混凝土抗压强度影响最大，其原因是：自由流体饱和度代表着大孔的数量，总体孔隙中大孔隙占比越大，说明随着冻融循环次数的增加，混凝土裂缝、孔隙越多。

3.2 建立GM（1，3）模型

依据表4数据，选取自由流体饱和度和少害孔孔隙占比和抗压强度建立GM（1，3）模型。为得到GM（1，3）模型，需要对数据进行计算处理，设原始序列为$ X_i^{(0)} $=（$ X_i^{(0)} $(1), $ X_i^{(0)} $(2)$,\cdots , $ $ X_i^{(0)} $(n)），一阶累加（1-AGO）序列设为$ X_i^{(1)} $=（$ X_i^{(1)} $(1), $ X_i^{(1)} $(2)$,\cdots , $ $ X_i^{(1)} $(n)），其中，$ X_i^{(1)} $(n)=$ \displaystyle \sum\limits_{i = 1}^n {x_i^{(0)}} (i) $，$ X_1^{(1)} $的紧邻均值序列设为Z₁⁽¹⁾=（Z₁⁽¹⁾(1), Z₁⁽¹⁾ (2),···,Z₁⁽¹⁾(n)），其中，Z₁⁽¹⁾(n)= $ {[{x_1^{(1)}(n - 1) + x_1^{(1)}(n)}]}/{2} $。$ X_1^{(0)} $为不同冻融循环次数下混凝土的抗压强度，X_j⁽⁰⁾(j=2,3)是自由流体饱和度和少害孔孔隙占比，建立GM（1，3）模型为：

其中：p和q_j关联构成矩阵：p=[p q₂ q₃]^T，利用最小二乘法可得模型系数矢量方程为：p=(Q^TQ)^–1Q^TY。

通过计算，得到的模型即为预测抗压强度公式：

最后将试验结果与预测结果进行比对，得出两者之间的残差、相对误差绝对值如表5所示。由表可知，不同冻融循环次数下混凝土的GM（1，3）模型预测结果与试验结果的相对误差绝对值的平均值为0.29%，说明模型精度较高。因此，不同冻融循环次数下混凝土的抗压强度性能可以采用自由流体自由度和少害孔占比预测的抗压强度公式（7）进行结果预测。

4 冻融破坏机理分析

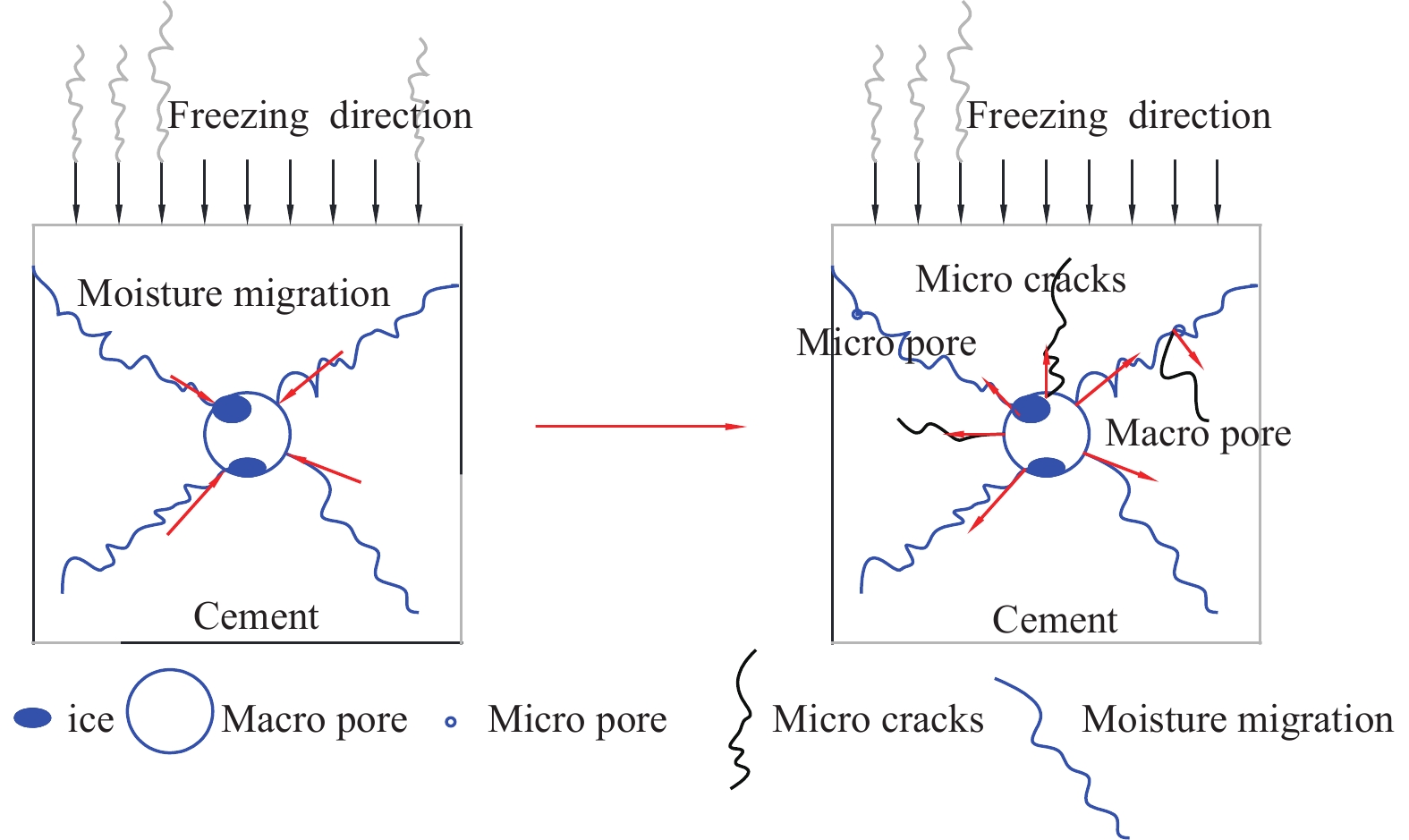
混凝土冻融循环破坏的主要原因是混凝土内部微裂缝的产生和不断扩展。研究表明，混凝土在冻融后吸水率显著增加，含水饱和度迅速增加^[18]。当温度降到0 ℃以下时，混凝土内部毛细孔中的水分会变成冰，体积膨胀约9%。在冻融循环过程中，水份逐渐向冻结产生的大孔隙周围迁移，孔隙溶液的迁移最终产生静水压和渗透压。当膨胀力超过毛细管壁的抗拉强度时，微裂缝开始在周围扩展并逐渐渗透到混凝土内部。在静水压力作用下，大孔隙表面首先被破坏，然后在大孔隙周围再生成新的孔隙。根据试验结果，图8所示为冻结过程中混凝土劣化过程中不同尺寸孔隙中水分迁移的概念模型。

5 结束语

1）冻融循环200次抗压强度损失达到56.4%，动弹性模量损失达到61.72%。

2）冻融循环200次时，T₂谱总面积增加了4.02倍，第一峰面积占比减小了34.25%。

3）随着冻融循环次数的增加，无害孔和少害孔占比减小，有害孔和多害孔占比增大，混凝土孔隙度增大。

4）通过灰熵关联度分析，混凝土中的自由流体饱和度和少害孔孔隙占比最大，分别为0.9893和0.9952，两者对不同冻融循环下的抗压强度影响最大。GM（1，3）建立了混凝土抗压强度、自由流体饱和度和少害孔之间的模型，模型预测值与试验值的平均相对误差为0.29%。最后，建立了基于孔隙率变化的损伤模型，定量描述了宏观力学性能的退化规律，与试验结果吻合较好。

5）研究结果可为寒冷地区混凝土结构的耐久性预测和安全性评估提供数据支持和参考。为了提高混凝土结构在寒冷气候下的耐久性和使用寿命，应降低孔隙率。