0 引　言

双弯弯管作为输配流体管网系统中重要部件，广泛地应用于水利、农业灌溉、建筑、化工、航空航天等行业^[1]。由于边界条件改变，流体在弯管中流动，受离心力和惯性力影响，其内部流场发生变化，形成二次流^[2]，消耗主流能量，造成水头损失与振动，影响输配管网系统运行稳定性。许多学者通过试验和数值模拟^[3]对弯管的流动特性进行了研究。实验研究方面，贺益英等^[4-6]研究了90°组合弯管流动特性，得出影响弯管局部阻力系数的因素，拟合了其函数关系。数值模拟方面，王永成^[7]研究表明在相同条件下，45° Z型弯头比90°弯头压降减少约40%。叶飞、张昕、孙业志等^[8-10]研究了雷诺数、曲率半径、粗糙度对90°弯管局部阻力系数以及二次流的影响。实验研究与数值模拟结合方面，杨湘隆等^[11]采用不同湍流模型对 90°大曲率圆形截面弯管内的湍流流动进行了计算模拟，表明RNG$ k $-$ \varepsilon $模型模拟效果与试验结果最为吻合。陈晓等^[12]对90° Z型组合弯管局部阻力特性进行了研究，阐明了组合弯管的相对间距对弯管局部阻力影响起主要作用。以往研究主要集中于直角弯管或直角组合弯管，对于不同结构双弯弯管水动力特性研究较少。本文采用CFD^[13]对不同夹角、流道结构组合形式、雷诺数下的DN192 mm双弯弯管水力性能进行数值计算，分析其水头损失与水力特性，对双弯弯管流道结构进行优化，得到节约能耗的最佳角度，以期为双弯弯管设计提供理论依据。

1 材料与方法 1.1 弯管几何参数

本文使用Solidworks2019建立不同组合模型，θ为入流方向与过渡段夹角，取值为π/12、π/6、π/4、π/3、5π/12、π/2。尺寸参考文献[6]，管内径D为192 mm，弯管的相对弯曲半径R/D=1，入、出口与中心线距离L、上下管中心线距离H长度都为3D，模型流道结构如图1所示。

1.2 弯管模型建模

1.2.1 模型网格划分

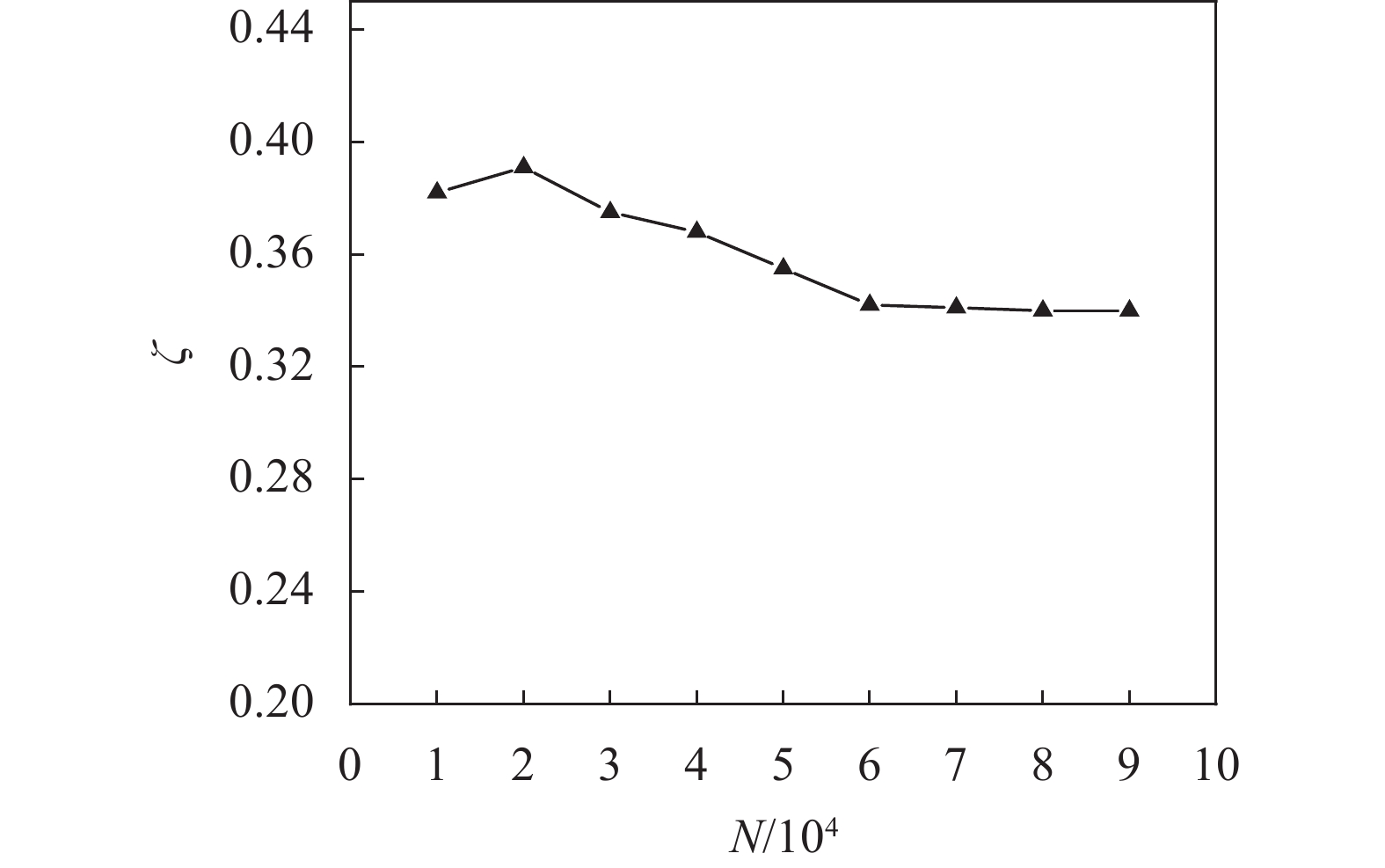
采用ICEM对模型进行结构化网格划分，网格质量全部在0.6以上，满足计算需要。为了验证网格划分的合理性，取速度为1.0 m/s，网格划分参数进行优化，网格尺寸设为20 mm，当网格数为6×10⁴左右时，随着网格数目的增加，局部阻力系数趋于稳定，以该种情况下的网格参数进行计算，网格划分与无关性验证见图2和图3。

1.2.2 计算数学模型

弯管内部流动介质为水，在常温下为不可压缩流体，文献[2]分别用Standard$ k $-$ \varepsilon $模型、RNG$ k $-$ \varepsilon $模型、Realizable$ k $-$ \varepsilon $模型对90°弯管进行数值模拟，并将模拟值与实验值进行对比，结果发现采用RNG$ k $-$ \varepsilon $模型计算出来的结果与实验值更为接近，因此本次模拟计算采用RNG$ k $-$ \varepsilon $^[14]模型。

1.3 求解方法与边界条件

1.3.1 求解方法

采用三维稳态模型进行求解，Y方向设置重力加速度为–9.81 m/s²。采用SIMPLE算法进行迭代计算，压强和动量方程均采用二阶迎风格式，残差收敛值设为10^–4。

1.3.2 边界条件

入口边界条件设为速度入口，速度分别设置为V₁=0.1 m/s、V₂=0.5 m/s、V₃=1.0 m/s、V₄=2.0 m/s、V₅=4.0 m/s。相应雷诺数为Re₁=0.192×10⁵、Re₂=0.96×10⁵、Re₃=1.92×10⁵、Re₄=3.84×10⁵、Re₅=7.68×10⁵。水体温度为20 ℃，运动粘度1.0$ \times $10^–6 m²/s，出口边界条件设为自由出流，壁面采用无滑移边界条件，湍流定义方法采用湍动能强度I和水力直径D。Re=Vd/$ \nu ，I=0.16\times {Re}^{-1/8} $，其中Re为雷诺数；V为管道平均流速，m/s；$ d $为管道内径，m；$ \nu $为运动粘滞系数，m²/s。

2 结果与分析 2.1 可靠性分析

双弯弯管模型管径较小，长度较短，忽略沿程阻力损失系数，局部阻力损失系数如下^[15]：

式中：Z——位置水头，m；

P——压强，N/m²；

γ——单位体积的重量，kg/（m²·s²）；

V——流体流速，m/s；

${h}_{\rm w}$——水头损失，m；

$ \zeta $——局部水头损失系数。

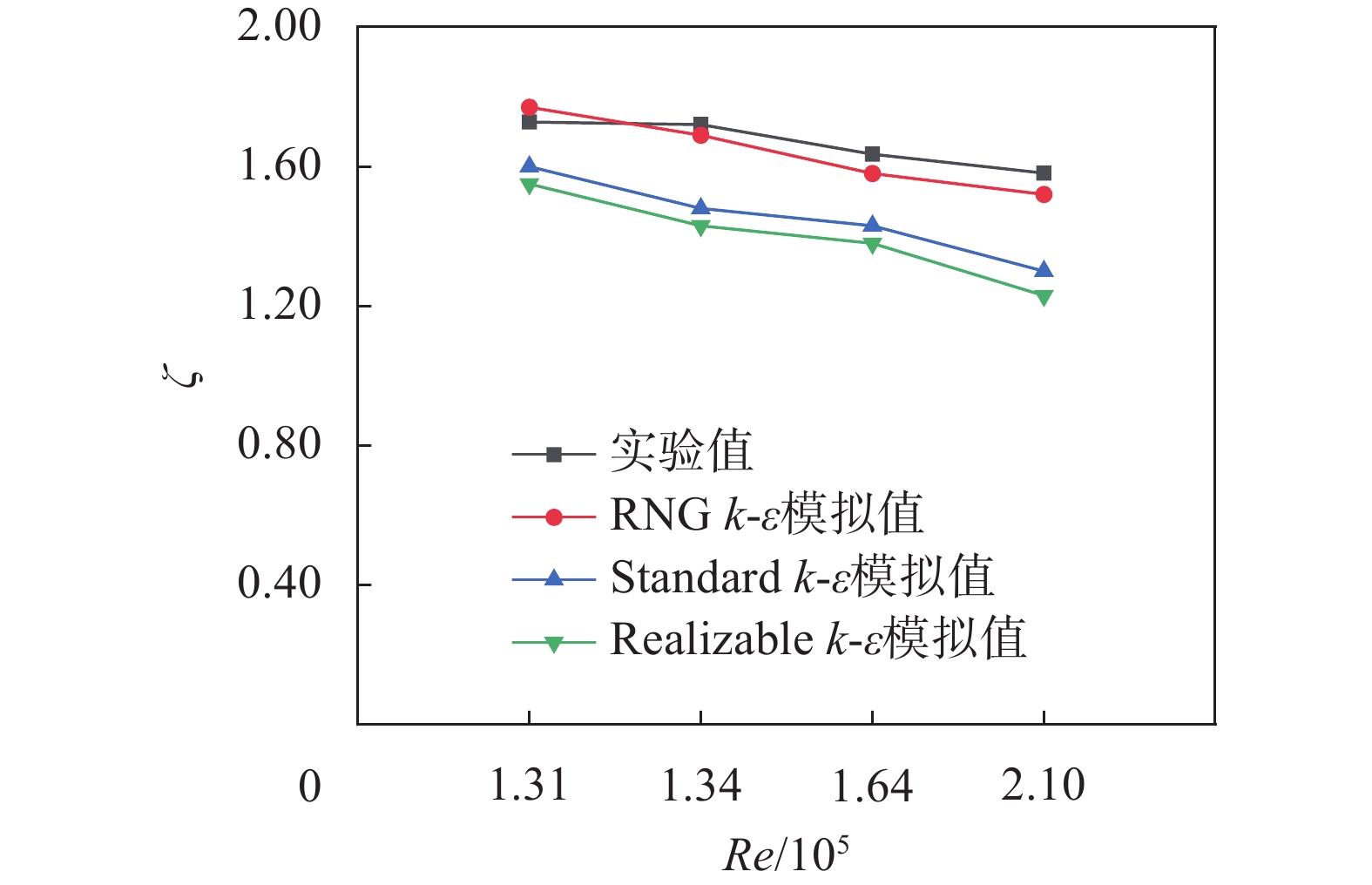
为了验证模拟可靠性，取文献[9]中相对弯曲半径为1的90°弯管中的实验数据与3种模拟数据进行对比。由图4可知，3种模型模拟值都与实验值相差较小，但总体上RNG k-ε模拟值与实验值吻合最好，全部误差在5%以内，说明用RNG k-ε模型对弯管进行模拟具有可靠性。

2.2 弯管组合局部水力特性分析

2.2.1 不同雷诺数对局部水头损失的影响

根据图5可得，局部阻力损失系数随着雷诺数的增大呈逐渐减小的趋势，这是因为流体运动同时受黏性力和惯性力的影响，当雷诺数较小时，黏性力对流体运动起主导作用，此时管内流体与壁面的摩擦阻力较大；当雷诺数较大时，惯性力对流体运动起主导作用，此时管内流体与壁面的摩擦阻力较小。还能看出，相比弯折、折弯、折折组合而言，弯弯组合弯管局部阻力损失系数随雷诺数增大而下降的趋势更加明显，说明弯弯组合弯管随着雷诺数的增加所减少的局部水头能量损耗更加显著。

根据最小二乘法原理，将双弯弯管局部阻力系数计算结果进行回归分析，得到最佳数学表达式如表1所示。由表可知，所有组合弯管的局部阻力损失系数ζ随夹角θ均呈二次抛物线关系，相关系数都在0.94以上。

2.2.2 不同角度对局部水头损失的影响

根据图6可得，所有组合弯管局部阻力损失系数都随着角度增大先减小后增加，局部阻力损失系数达到最小值前，局部阻力系数弯弯组合降低幅度最大，达到最小值后增加幅度最小。所有组合弯管在角度为π/6时，局部阻力损失系数达到最小，说明DN192 mm双弯组合弯管入流方向与过渡段夹角应在π/6左右为宜。

通过对不同组合、不同雷诺数下局部阻力损失系数ζ与夹角θ关系进行回归分析，结果表明所有组合弯管的局部阻力损失系数ζ随弯曲角度θ都呈二次抛物线关系，相关系数都在0.97以上，如表2所示。

2.2.3 不同组合对局部水头损失的影响

为了研究同一雷诺数下不同组合弯管的局部阻力系数变化情况，得到局部阻力系数随不同组合弯管变化曲线图如图7所示。所有组合弯管中，弯弯组合弯管局部阻力系数最小。当夹角θ为π/12时，弯折、折弯、折折组合弯管局部阻力系数无明显变化；当夹角θ大于π/12时，折折组合弯管局部阻力系数最大，弯折、折弯组合弯管局部阻力系数基本相同，弯折与折弯组合局部阻力系数是弯弯组合的1.15~2.9倍，而折折组合局部阻力系数是弯折与折弯组合的1.02~2.12倍。由此说明，相同条件下，在双弯弯管设计过程中，弯弯组合弯管结构最好，而弯折、折弯组合较好，折折组合最差。

2.2.4 不同组合对局部水头损失差异系数影响

为了讨论不同夹角、不同雷诺数情况下，不同弯管组合局部水头损失变化情况，得到较为合理的弯管组合设计方案：定义λ为局部水头损失的比值，其表征含义为不同弯管组合的流道结构或形状因子造成的局部水头损失差异系数，如表3所示。

由图8可以看出，Re相同的情况下，λ均随着角度增大而变小，到π/2达到最小。相同的角度情况下，λ₄＞λ₆＞λ₂＞λ₃；λ₁与λ₂，λ₅与λ₆几乎没有差异。说明DN192 mm双弯弯管设计过程中，弯弯组合弯管结构比弯折、折弯、折折组合弯管都要好，而弯折、折弯组合又比折折组合要好，弯折组合与折弯组合差别不大，并且这种优势随着角度增加而更加凸显。故在设计双弯弯管的时候应该优先考虑弯弯组合。

2.3 弯管组合流场特性分析

为了探究不同弯管组合流场特性，利用tecplot软件对计算结果进行后处理，选择雷诺数为1.92×10⁵工况为例，截取不同弯管组合、不同夹角中纵剖面进行压力场分析，两个弯头进出口过渡断面进行流线与速度场分析，距离弯管出口距离为D处进行湍动能分析。

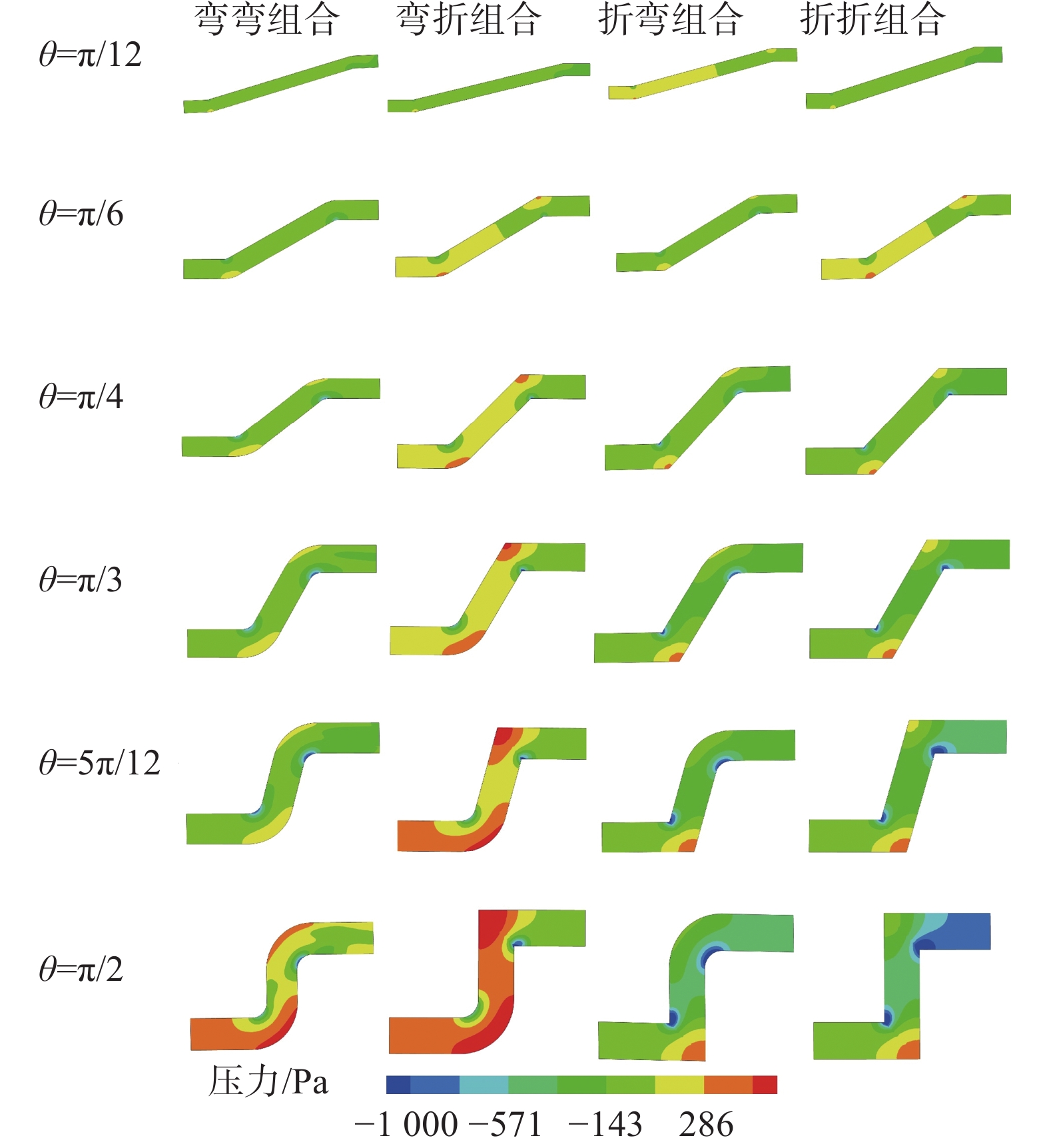
2.3.1 不同组合压力场分析

根据图9可得，不同弯管组合，弯管凸侧压力小于凹侧压力，凹凸侧附近压力分布变化较明显，其他地方压力分布较均匀，这是由于流体在直管段流动时，管道局部边界急剧改变，造成主流与壁面发生脱离，促使水流结构、流速分布也发生变化，主流偏向弯管凹侧，弯管凸侧出现负压，流体受惯性作用，对管道壁面造成冲击，凹侧管壁受到的压力增大，消耗能量。经过第一段弯管后，局部边界对流态变化影响减弱，主流运动方向恢复，压力分布也恢复到均匀分布状态。经过第二段弯管后，边界再一次发生改变，导致主流方向第二次改变，主流能量进一步减少，但压强改变量明显小于第一次压力改变量，主要受流体初始动能影响。相同的弯管组合，随着弯曲角度θ的逐渐增大，能量损耗逐渐增大，同时压强变化也在增大，主要原因是角度越大，需要克服流体的惯性力也增大，需要能量就更多。4种组合中，折折组合压强变化梯度最大，弯弯组合变化梯度最小，主要是折折组合流道结构造成的，因为流体经过折折组合折角处与管壁进行碰撞，而弯弯组合为光顺过渡，顺流体流动方向，有利于流体运动。故在进行DN192 mm双弯管设计时应当合理选择入流与出流方向与过渡段中心线夹角，并对流体运动方向改变的管段进行优化，最大限度避免造成较大能量损耗，并且在凹侧采取适当的加固措施，防止压力过大造成管壁破坏。

2.3.2 不同组合流线及速度场分析

根据图10可得，不同弯管组合流线分布均较均匀，随着角度增大，折弯附近速度变化明显，速度部分变化差异明显的区域随着角度变化有增大的趋势。对于弯弯组合，受离心力的作用下，弯管凹侧流体与壁面发生分离现象，主流被压迫，能量耗散，在横断面上会产生迪恩涡^[16]。流体经过第一个弯头时，横断面上出现二次流，二次流的中心向凹侧聚集，横断面上流线分布均匀。在中间直管段内流线分布较为均匀，经过第二个弯头后，流体主流方向靠近凸侧，并且流线向凸侧进行聚集，在第二个弯头右侧产生回流区，增加流体与壁面的撞击、摩擦，水分子相互掺杂，主流能量耗损，造成水头损失。对于弯折组合与折弯组合，当弯曲角度小于π/4，横断面上二次流不明显，弯曲角度大于等于π/4，横断面上出现二次流。对于折折组合，弯曲角度大于π/3时，流体经过第二个弯头，横断面上出现二次流。故对双弯弯管设计时，折角处应该尽量用圆角替换尖角，并充分考虑角度对二次流的影响，选取合适的弯曲角度。

2.3.3 不同组合湍动能分析

由图11与表4可得，最大湍动能在[0.008 J, 0.018 J]区间之内变化，湍动能最大位置均靠近壁面位置。弯弯组合湍动能分布比其余组合变化更为明显，湍动能最大值为0.018 J，湍动能最大值中心由凹侧向凸侧进行偏移；弯折组合在中心线下侧折弯右侧靠近壁面位置；折弯组合在靠近凹侧近壁面位置；折折组合在中心线上侧折弯靠近壁面处。主要原因是靠近壁面，速度变化梯度较大，流层受流体与壁面之间的剪切力影响越大。弯弯组合中，最大湍动能随着角度的增大而增大；弯折、折弯、折折组合中，最大湍动能随角度增大变化不明显。说明最大湍动能受不同弯管组合流道结构的影响，湍动能增大，流体所受到的扰动加强，能量损耗加剧，故在设计弯弯组合弯管应当选择适宜的角度，降低能量损失。

3 结束语

本文通过Solidworks2019对DN192 mm双弯弯管建立不同夹角、流道结构下的物理模型，采用计算流体动力学CFD软件进行数值模拟，在验证模拟可靠性的前提下，探讨了夹角、流道结构、雷诺数对局部阻力系数的影响，揭示了双弯弯管内部的速度、压力湍动能分布情况，得出以下结论：

1）双弯组合弯管的局部阻力系数随着夹角增大呈二次抛物线关系变化，且在角度为π/6时达到最小。

2）相同条件下，在双弯弯管设计过程中，弯弯组合弯管结构最好，而弯折、折弯组合较好，折折组合最差。

3）在实际生活输配流体或组合弯管设计中，针对DN192 mm双弯弯管结构入流方向与过渡段夹角应在π/6 左右为宜。