文章信息
- 蔡国军, 卫俊仁, 杨森林, 蒲洪, 李林
- CAI Guojun, WEI Junren, YANG Senlin, PU Hong, LI Lin
- 磷石膏动模量及阻尼比试验研究
- Experimental study on dynamic modulus and damping ratio of phosphogypsum
- 中国测试, 2024, 50(5): 11-18
- CHINA MEASUREMENT & TEST, 2024, 50(5): 11-18
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022020058
-
文章历史
- 收稿日期: 2022-02-20
- 收到修改稿日期: 2022-05-06
2. 成都理工大学地质工程国家级实验教学示范中心,四川 成都 610059
2. National Geological Engineering Experimental Teaching Demonstration Center of Chengdu University of Technology, Chengdu 610059, China
随着我国磷酸产业的迅速扩大,国内磷石膏年均产量越来越大,截至2020年,磷石膏年产量已经达到了7500万吨,累积堆存量达到6亿多吨,面对如此高的产量,国内对于磷石膏的利用率却较低,仅为40%左右,制作石膏板被作为磷石膏废渣的主要利用方式;利用途径和利用率远不及西方等国家[1-2]。我国磷石膏废渣每年净增量超过5000万吨,与此同时,磷石膏由于其特殊的化学成分及特性,长期堆存会对环境造成污染[3]。国内堆存磷石膏的方法主要有两种,依据工艺和制作流程不同,分为了干堆法和湿堆法。通过磷石膏废渣的不断堆存,形成了磷石膏尾矿库,且尾矿库坝体不断加高。而西南片区地质条件复杂,地震多发,一旦失稳,会给库区下游带来不可估量的人身及财产损失。据资料显示,现有磷石膏堆积坝高可达到百米及以上,且有过数个堆积坝发生过溃坝事件[4]。
目前,国内已有许多对于尾矿动力特性的研究。张婷等[5]对尾粉土的动力性质做了研究,并提出了关于动剪模量和动模量衰减的修正公式。杨安银[6]考虑尾矿库的抗震特性,利用动三轴仪对尾矿库区内较为典型的尾粉土、尾粉黏土、尾细砂进行了动力试验,研究不同尾矿土地震荷载条件下的动力变形特性。但对于磷石膏的动力特性研究并不太多。米占宽等[7]、魏作安等[8]依据柳树菁磷石膏库,对磷石膏的物理特性进行了研究,并开展了磷石膏动静力特性试验,发现磷石膏整体强度要强于同等密实度下的粉土、粉砂土。路停等[9]利用GDS动三轴仪进行了磷石膏动力特性试验,得出了较低围压下磷石膏的动力学参数。根据李宝平[10]的研究,在实际工程场地中,随着土层厚度的不断增加,上覆荷载会不断提高,土体单元受到的应力状态多为偏压固结状态,随着磷石膏的不断堆存,磷石膏库的坝体不断升高,中下部土层的自重荷载提升,所以研究偏压固结下磷石膏动力特性对于磷石膏坝体及库区稳定性有重要意义。
场地上的工程建筑在被施加动荷载条件后,能否抵抗其破坏,很大程度上取决于工程场地中地基土层的自身条件,而评价场地中土层自身条件的因素之一,就是岩土体的动力特性[11-13]。所以工程师们引入了动模量(动弹性模量E、动剪切模量G)来评价其动力变形特性[14]。因此,研究土体初始模量以及模量的衰变关系十分必要。本文利用GDS动三轴仪,对磷石膏的动力学特性开展试验研究,分析其偏压固结条件下动模量以及阻尼比特性,以获得相关动力参数,为设计提供依据。
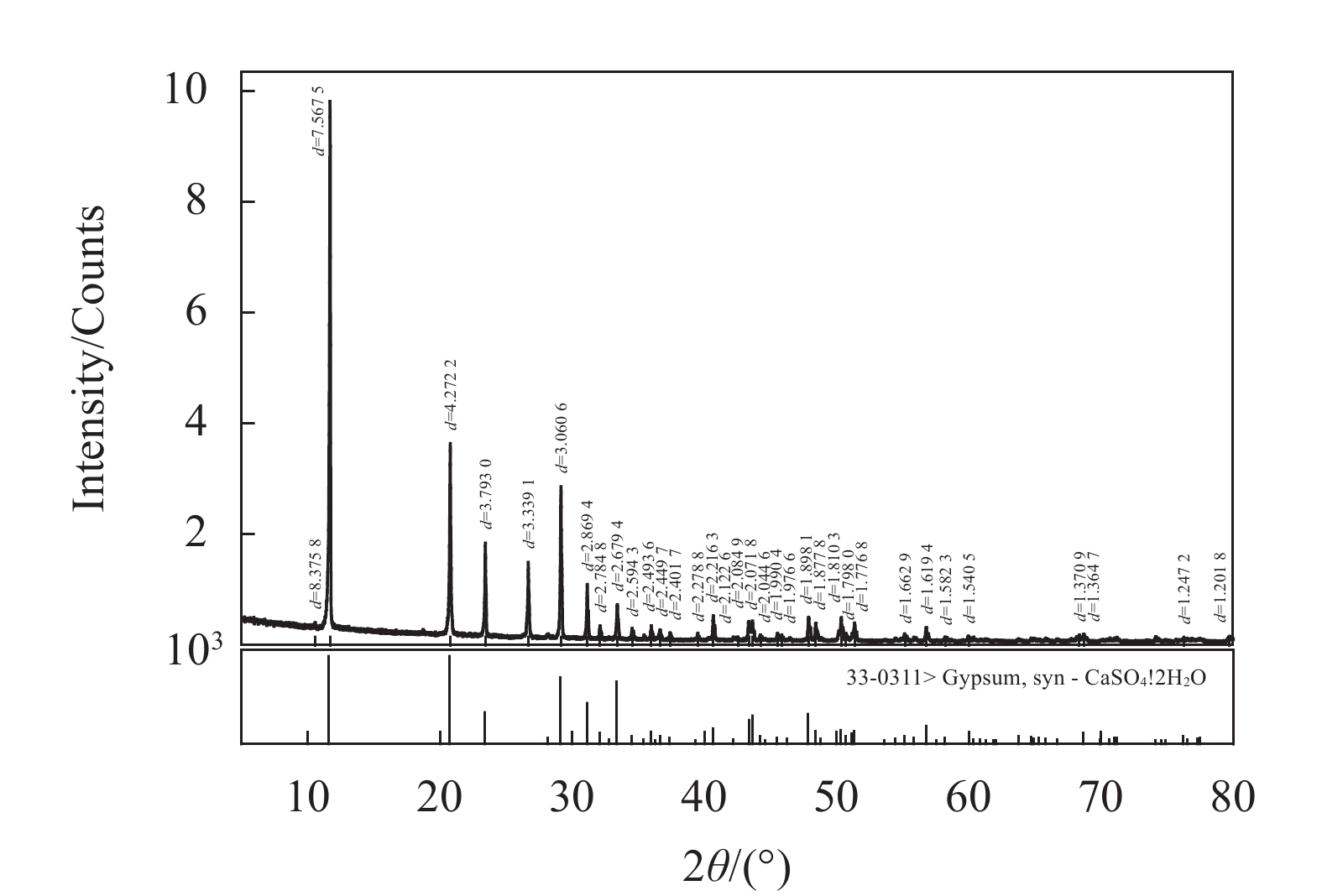
1 试样制备本次试验的样品取自杨家箐磷石膏堆场库区,磷石膏矿浆从管道湿法排放至库区上游,堆存析水后经过一段时间的自然沉积形成磷石膏废渣。经过调查发现,杨家菁库区内固结的磷石膏状态存在明显差别,分析其原因,是因为堆排时间存在先后差异,且含水量也对其造成了一定影响。利用全岩X射线粉晶衍射对其矿物成分进行分析(图1),得出该库区磷石膏样品主要成分为石膏和石英,比例分别为91%和9%。
|
| 图 1 矿物衍射分析图 |
本次实验试样均为扰动土样(图2),试样密度根据取土深度确定,见表1。按照GB/T 50123—2019《土工试验方法标准》等国家相关规程进行,因为磷石膏的主要成分为CaSO4·2H2O[15],所以磷石膏内含有较多结晶水,在烘干时温度设定为40 ℃(±2 ℃),首次烘干时间大约为2 h。

|
| 图 2 磷石膏土样 |
本次试验采用湿装夯实法制样。制样前,将磷石膏试样按照一定含水率制成湿样,再放置于保湿缸内,浸润24 h,测定其含水率。根据所需要的干密度,进行分层击实。为了避免各层之间的分层现象,各层接触面均经过刻毛处理。然后将制好的土样放入真空饱和机进行饱和。之后,再进行饱和度B检测,当B值≥0.98时,即可开始施加应力固结。
2 试验仪器及方案本次试验仪器使用的是成都理工大学地质灾害防治与地质环境保护国家重点实验室的GDS-DYNTTS型微机控制振动三轴试验系统。试验试样尺寸为Φ100 mm×200 mm圆柱体,试验振动频率f为1 Hz。根据试验规程的要求,在试样饱和度B≥0.98时进行排水固结,对其施加1 Hz的轴向动荷载,同时关闭排水阀。由于模拟地震震动条件下的情况,土体内水无法及时排出,所以进行不排水试验。
本次试验选择偏压固结,磷石膏选取的干密度为1.40 g/cm3和1.50 g/cm3,偏压固结比Kc为1.5、2.0(Kc=σ1/σ3;σ3=200、400、600 kPa);详细试验方案如表2所示。偏压固结时,设定每个试样破坏标准为动应变εd=10%。
| 试样分组 | 干密度/(g·cm–3) | 含水率/% | 固结比 | 围压/kPa |
| 1 | 1.40 | 15.1 | 1.5、2.0 | 200、400、600 |
| 2 | 1.50 | 13.9 | 1.5、2.0 | 200、400、600 |
3 动模量及阻尼比特性分析 3.1 动模量
1) 动弹性模量Ed
磷石膏的动弹性模量为磷石膏在动荷载作用下动应力与动应变的比值,Hardin[16]的等效黏弹性模型为:
| $ {E}_{\mathrm{d}}=\frac{{\sigma }_{\mathrm{m}\mathrm{a}\mathrm{x}-}{\sigma }_{\mathrm{m}\mathrm{i}\mathrm{n}}}{{\varepsilon }_{\mathrm{m}\mathrm{a}\mathrm{x}-}{\varepsilon }_{\mathrm{m}\mathrm{i}\mathrm{n}}} $ | (1) |
根据式(1)计算出不同围压、密度、固结比下的动弹性模量Ed,并作出不同固结比和密度下

|
|
图 3
不同密度下 |

|
|
图 4
不同固结比下 |
随着围压的减小,曲线随之而向下移动,围压和固结比越大,土体之间的紧密性越好,其孔隙比小,使得土体颗粒之间能够发生更强的相互作用力,土体抵抗变形的能力就越好。围压相同的情况下,随着固结比增大,磷石膏的
2)最大动弹性模量Ed0
庄心善等[17]采用Kondner模型求取最大动弹性模量,其表达式为:
| $ \frac{1}{{E}_{\mathrm{d}0}}=a+b{\varepsilon }_{\mathrm{d}} $ | (2) |
如下所示,说明Kondner模型适用于磷石膏应变较小时的

|
|
图 5
不同密度下 |
3)动弹性模量比
动模量比(Ed/Ed0)曲线能够更好地反映动模量的变化趋势,将

|
|
图 6
不同密度下 |
在围压增加至600 kPa以后,曲线发生一定的向右移动,说明对于密实度低于92%的磷石膏土,增加有效应力可以在一定程度上抵抗动弹性模量的迅速衰减。值得指出的是,虽然固结比的增大会使磷石膏动模量的大小有较小幅度的提高,但这种影响并不适用于各级围压下的情况,推测在低围压(0~400 kPa)下,固结比越大会对磷石膏抵抗动模量的衰减起到一定作用,而当围压继续在增大时,固结比带来的影响便没有那么明显。
对动模量比的衰减模型进一步分析,利用Darendeli模型[18],如下式所示:
| $ \frac{{E}_{\mathrm{d}}}{{E}_{\mathrm{d}0}}=\frac{1}{1+{\left(a{\varepsilon }_{\mathrm{d}}\right)}^{b}} $ | (3) |
其中a、b均为拟合系数。
依据式(3)模型对磷石膏动模量比进行非线性拟合,可得出:
| $ \frac{{E}_{\mathrm{d}}}{{E}_{\mathrm{d}0}}=\frac{1}{1+{\left(5.2{\varepsilon }_{\mathrm{d}}\right)}^{0.92}} $ | (4) |
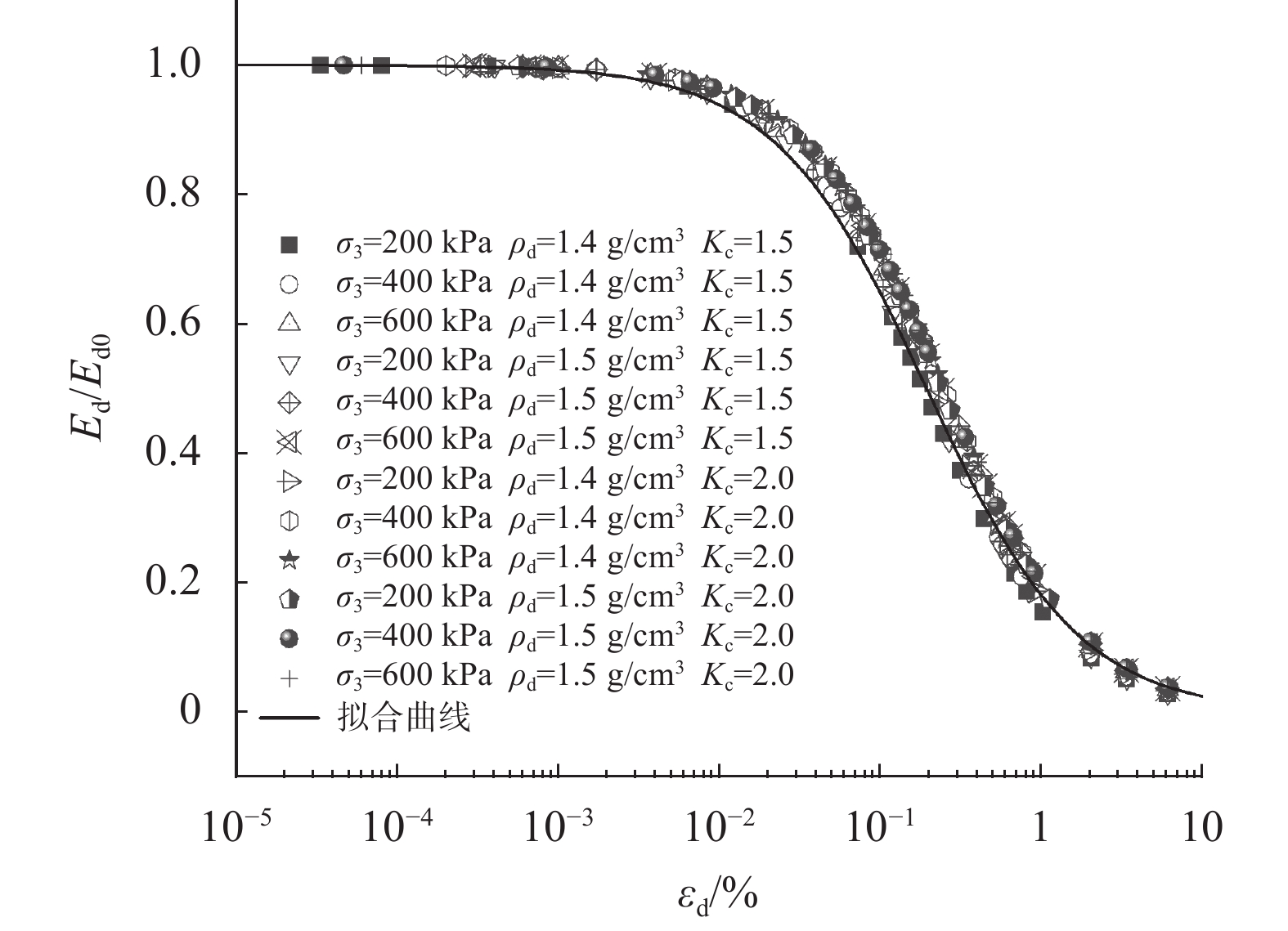
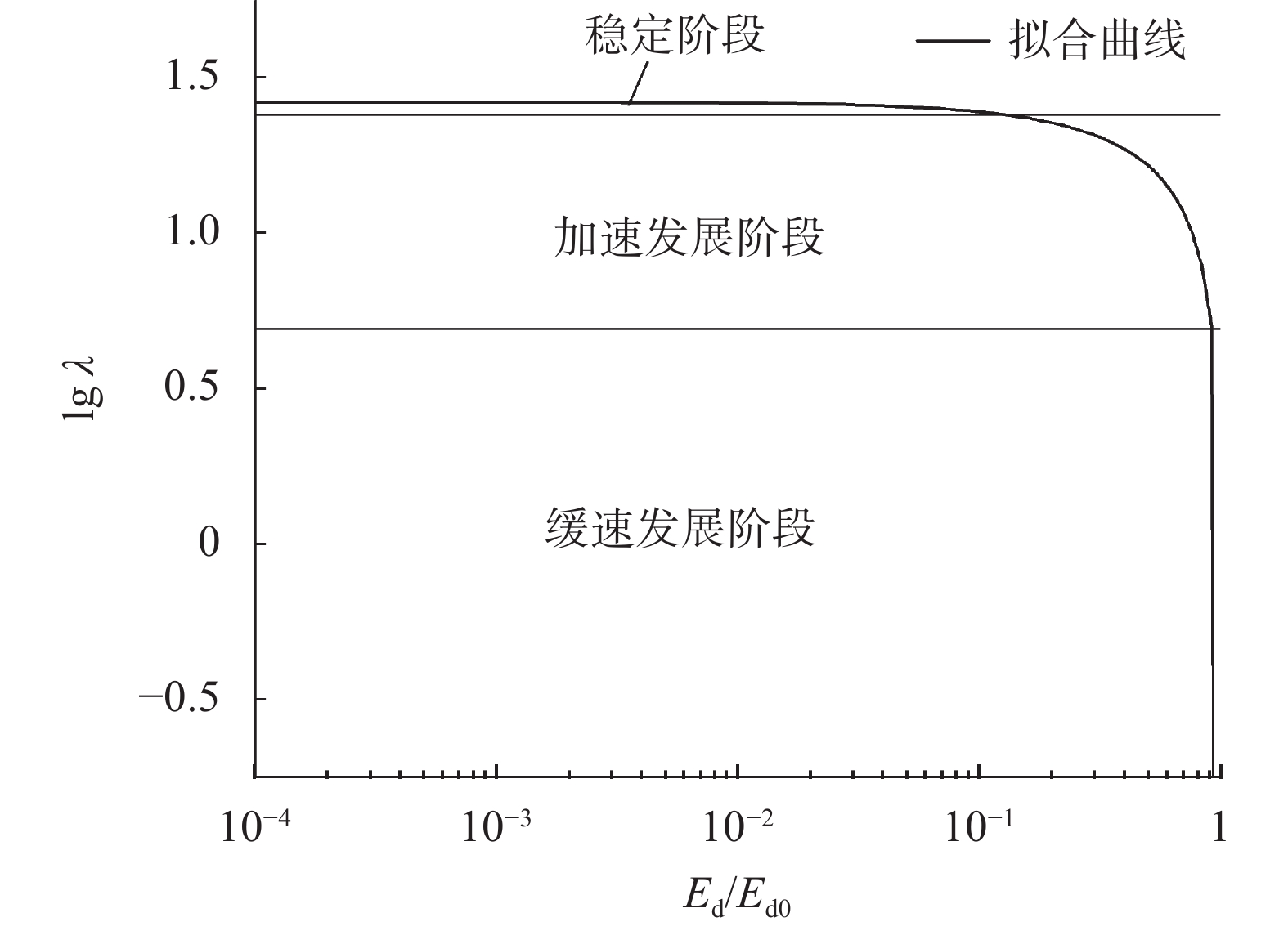
其拟合度参数如表3所示,拟合结果见图7。参数结果中r2均大于0.97,可见,该模型能够反映磷石膏的动弹性模量比衰减变化。将动弹性模量衰减划分为稳定、加速、衰退区3个阶段,如图8所示。衰变稳定阶段,动模量几乎不产生衰减,随着动应变增大而保持平稳或微弱减小;加速阶段,当动应变超过阈值后,动模量呈现出急剧衰减趋势(磷石膏的稳定-加速阈值为
| 密度/(g·cm–3) | 围压/kPa | 固结比 | a | b | r2 |
| 1.4 | 200 | 1.5 | 0.92 | 5.2 | 0.99828 |
| 1.4 | 400 | 0.92 | 5.2 | 0.99795 | |
| 1.4 | 600 | 0.92 | 5.2 | 0.9934 | |
| 1.5 | 200 | 0.92 | 5.2 | 0.99878 | |
| 1.5 | 400 | 0.92 | 5.2 | 0.99282 | |
| 1.5 | 600 | 0.92 | 5.2 | 0.99167 | |
| 1.4 | 200 | 2.0 | 0.92 | 5.2 | 0.99672 |
| 1.4 | 400 | 0.92 | 5.2 | 0.98207 | |
| 1.4 | 600 | 0.92 | 5.2 | 0.97577 | |
| 1.5 | 200 | 0.92 | 5.2 | 0.98737 | |
| 1.5 | 400 | 0.92 | 5.2 | 0.98003 | |
| 1.5 | 600 | 0.92 | 5.2 | 0.9742 |
|
| 图 7 磷石膏动模量比与动应变关系 |

|
| 图 8 磷石膏动模量比衰减分区 |
3.2 阻尼比
土体在受到动荷载作用时,应力应变关系常常呈现出滞后效应。这是因为土体在受到外部荷载时,颗粒间会产生摩擦,有一定的能量被消耗[19]。因此,需要一个指标来表征土体的能量耗散。此时引进一个参数指标,即阻尼比
| $ \lambda =\frac{1}{4\pi }\times \frac{A}{{A}_{\mathrm{s}}} $ | (5) |
式中:
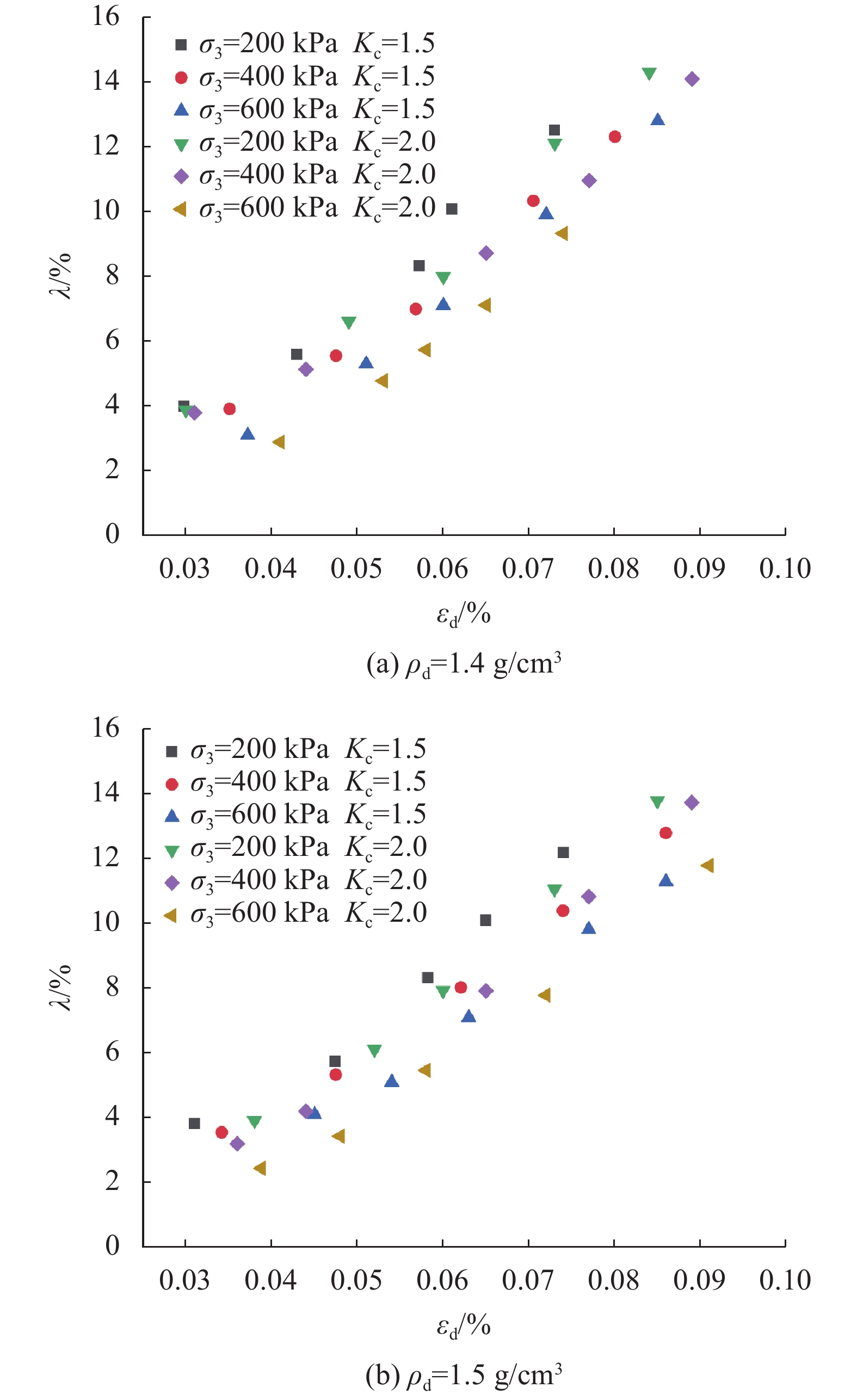
计算阻尼比
|
|
图 9
|
可以发现,随着固结比和围压的增大,磷石膏的阻尼比曲线下沉,说明对于较高围压,磷石膏对于动荷载的动力响应更加及时,在动应变
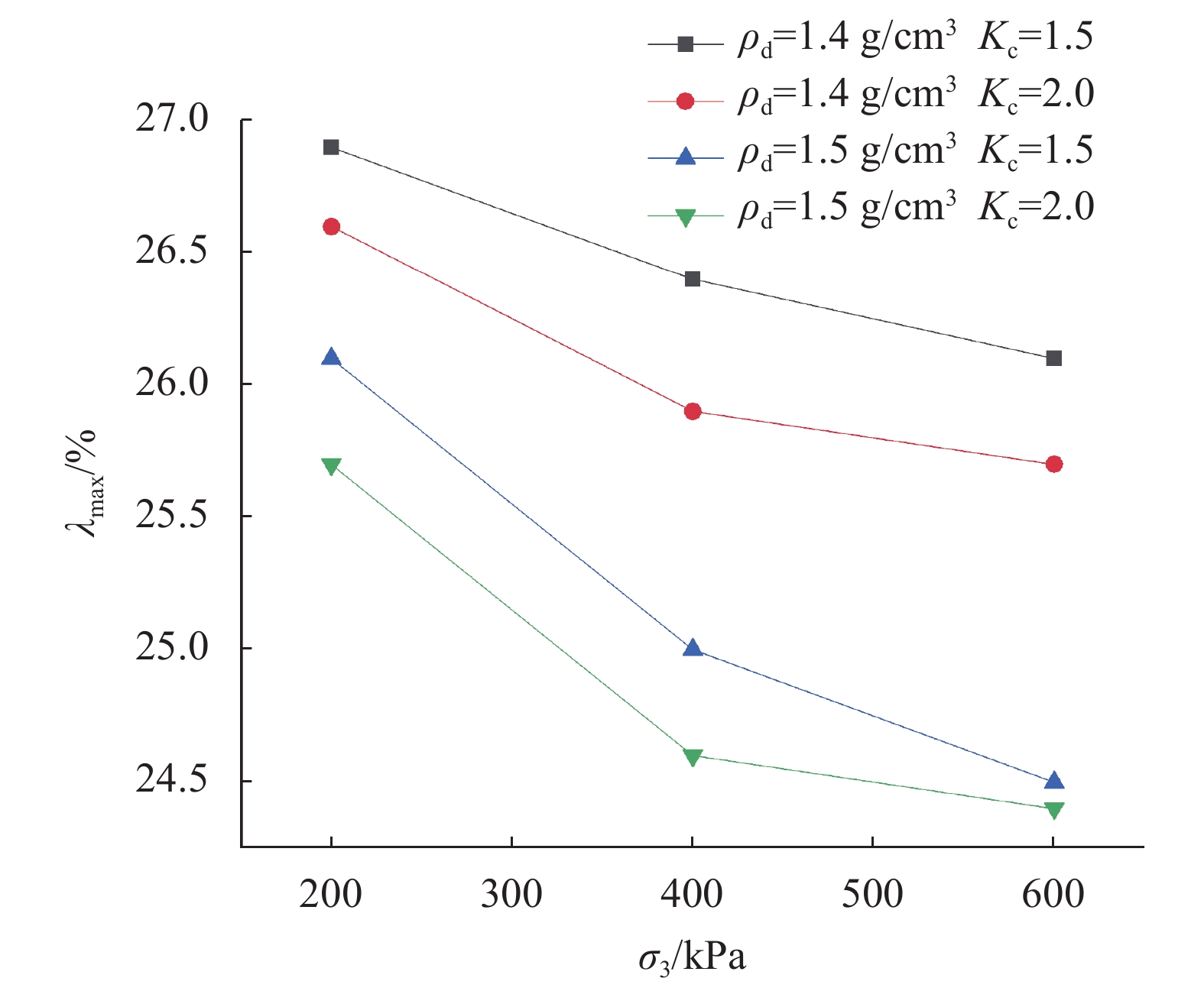
当
|
|
图 10
|
| $ \lambda ={\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}{\left(1-\frac{{E}_{\mathrm{d}}}{{E}_{{\mathrm{d}}_{0}}}\right)}^{n} $ | (6) |
| $ \mathrm{l}\mathrm{g}\lambda ={\mathrm{l}\mathrm{g}\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}+n\mathrm{l}\mathrm{g}\left(1-\frac{{E}_{\mathrm{d}}}{{E}_{{\mathrm{d}}_{0}}}\right) $ | (7) |
式中:
n——拟合参数。
可以发现在不同围压、固结比、密度等条件下
| $ \mathrm{l}\mathrm{g}\lambda ={\lambda }_{\mathrm{m}\mathrm{a}\mathrm{x}}+0.687\times \mathrm{l}\mathrm{g}\left(1-\frac{{E}_{\mathrm{d}}}{{E}_{{\mathrm{d}}_{0}}}\right) $ | (8) |
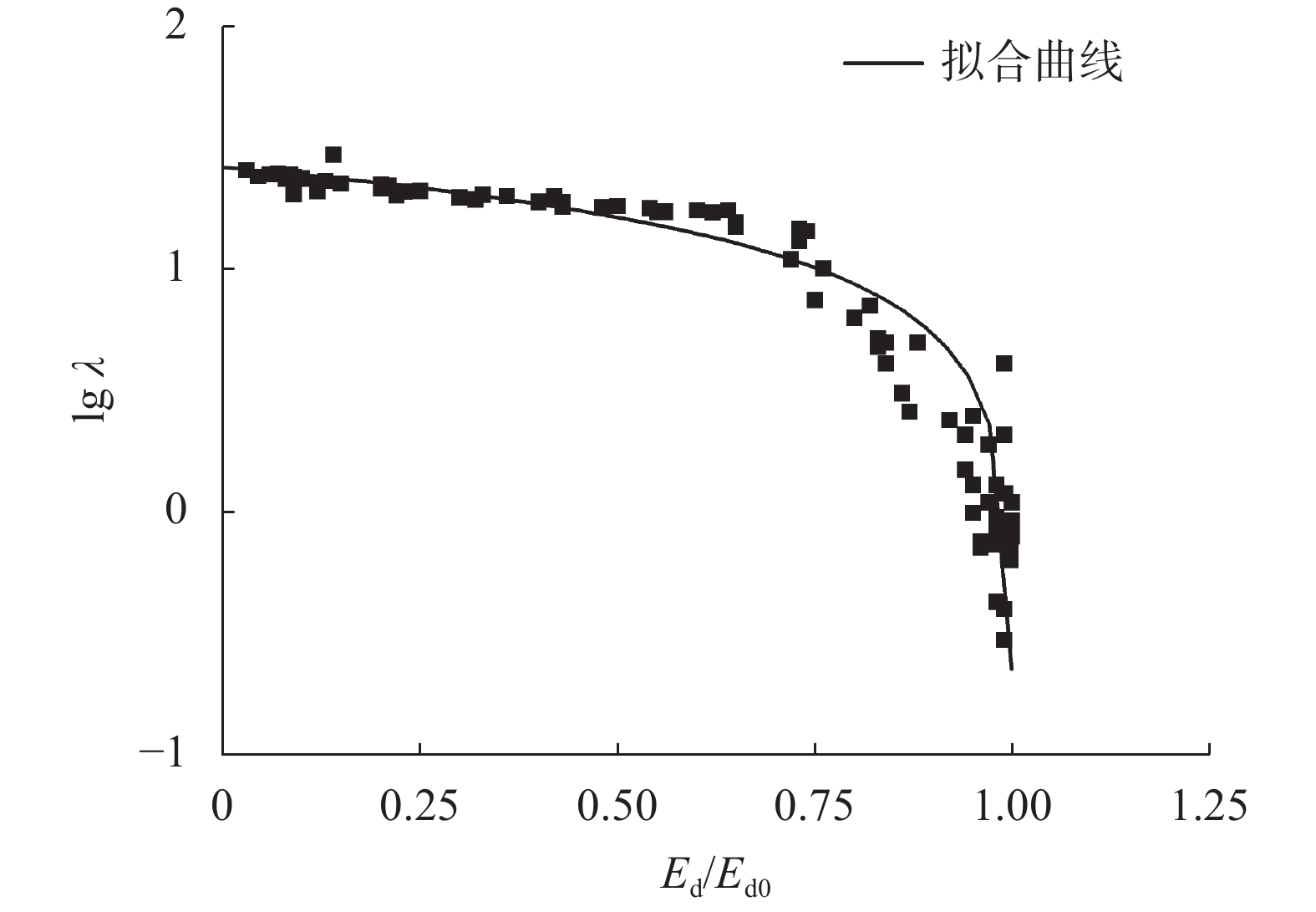
计算并拟合出回归曲线,如图11所示。由图可知,按
|
|
图 11
|
|
|
图 12
磷石膏 |
根据米占宽等[7]所得出的结论,库区内的磷石膏整体上为级配不良的粉土,有少部分为粉砂-中砂土,所以将磷石膏与尾矿库区中常见的尾粉砂、尾粉土进行对比[19-21],粉砂和尾粉土的最大阻尼比在0.25~0.30之间,磷石膏最大阻尼比要小于前者的10%左右;几种土的阻尼比都随着动应变
1)磷石膏的动弹性模量随着动应变增大而减小,当0.01%<
2)围压越大,磷石膏的最大动模量就越大,动模量衰减的速率和幅度也越大;对于密度的小幅改变,磷石膏最大动模量的变化并不敏感。
3)在围压小于400 kPa时,提高围压可以有效增强磷石膏抵抗动模量衰减的能力,提高密实度同样可以增强其抗动模量衰减能力。
4)本次试验磷石膏土样最大阻尼比范围在0.24~0.28,围压和固结比越大,最大阻尼比越小。利用最小二乘法对
5)本文通过对磷石膏尾矿开展动模量及阻尼比特性试验研究,为研究尾矿堆积坝在地震作用中的动力响应特性提供了经验参数;在实际工程中,能为后续的矿坝稳定性分析、设计提供理论支撑。
| [1] |
陈秋松, 张琦, 齐冲冲, 等. 磷石膏充填体强度和浸出毒性的温变规律[J].
中国有色金属学报, 2021, 31(4): 1084-1095.
CHEN Q S, ZHANG Q, QI C C, et al. Temperature-depending characteristics of strength and leaching toxicity of phosphogympsum-based cemented paste backfill[J].
The Chinese Journal of Nonferrous Metals, 2021, 31(4): 1084-1095.
DOI:10.11817/j.ysxb.1004.0609.2021-39736 |
| [2] |
张利珍, 吕子虎, 张永兴, 等. 磷石膏提质降杂实验研究[J].
无机盐工业, 2021, 53(6): 171-173.
ZHANG L Z, LÜ Z H, ZHANG Y X, et al. Experimental study on improving quality and reducing impurity of phosphogypsum[J].
Inorganic Chemicals Industry, 2021, 53(6): 171-173.
DOI:10.19964/j.issn.1006-4990.2020-0397 |
| [3] |
索崇娴, 曹洪雨, 曹家玮, 等. 赤泥-电石渣-磷石膏固化铜污染土性能[J]. 环境科学学报, 2021, 41 (11): 4686-4693.
SUO C X, CAO H Y, CAO J W, et al. Performance of red mud-calcium carbide residue-phosphogypsum solidified copper contaminated soil[J]. Acta Scientiae Circumstantiae, 2021, 41 (11): 4686-4693.
|
| [4] |
褚学伟, 许模, 王中美. 某磷石膏尾矿库堆积坝渗透稳定性分析[J].
工程地质学报, 2016, 24(4): 661-667.
CHU X W, XU M, WANG Z M. Stability analysis of seepage on the accumulation dam of a phosphogypsum tailings[J].
Journal of Engineering Geology, 2016, 24(4): 661-667.
DOI:10.13544/j.cnki.jeg.2016.04.023 |
| [5] |
张婷, 谭凡, 杨哲. 尾矿粉土动力变形特性试验研究[J].
长江科学院院报, 2020, 37(12): 146-151.
DOI:10.11988/ckyyb.20190970 |
| [6] |
杨安银, 王光进, 杨春和, 等. 坝体动力抗震及尾矿动力特性分析[J].
中国安全生产科学技术, 2019, 15(4): 122-127.
YANG A Y, WANG G J, YANG C H, et al. Dynamic seismic analysis of dam body and analysis of dynamic characteristics of tailings[J].
Journal of Safety Science and Technology, 2019, 15(4): 122-127.
DOI:10.11731/j.issn.1673-193x.2019.04.019 |
| [7] |
米占宽, 饶徐生, 储学群, 等. 沉积磷石膏的物理力学特性试验研究[J].
岩土工程学报, 2015, 37(3): 470-478.
MI Z K, RAO X S, CHU X Q, et al. Physico-mechanical properties of deposition phosphogypsum[J].
Chinese Journal of Geotechnical Engineering, 2015, 37(3): 470-478.
DOI:10.11779/CJGE201503010 |
| [8] |
魏作安, 路停, 李世龙, 等. 磷石膏物理力学性质的试验研究[J].
非金属矿, 2020, 43(2): 34-37.
WEI Z A, LU T, LI S L, et al. Experimental study on physical and mechanical properties of phosphogypsum[J].
Non-Metallic Mines, 2020, 43(2): 34-37.
DOI:10.3969/j.issn.1000-8098.2020.02.009 |
| [9] |
路停, 魏作安, 王文松, 等. 磷石膏的动力学特性试验研究[J].
振动与冲击, 2020, 39(14): 264-271.
LU T, WEI Z A, WANG W S, et al. Experimental study on the dynamic characteristics of phosphogypsum[J].
Journal of Vibration and Shock, 2020, 39(14): 264-271.
DOI:10.13465/j.cnki.jvs.2020.14.036 |
| [10] |
李宝平, 杨倩, 张玉, 等. 初始固结应力对平面应变黄土剪切破坏特性影响[J].
水文地质工程地质, 2020, 47(5): 92-99.
LI B P, YANG Q, ZHANG Y, et al. Effect of initial solidification stress on shear failure characteristics of loess under the plane strain condition[J].
Hydrogeology and Engineering Geology, 2020, 47(5): 92-99.
DOI:10.16030/j.cnki.issn.1000-3665.201912058 |
| [11] |
黄兴建, 付小敏, 沈忠, 等. 三轴循环荷载下岩石动态特性参数研究[J].
中国测试, 2016, 42(7): 117-122.
HUANG X J, FU X M, SHEN Z, et al. Study on dynamic characteristic parameters of rock under triaxial cyclic loading[J].
China Measurement & Test, 2016, 42(7): 117-122.
DOI:10.11857/j.issn.1674-5124.2016.07.024 |
| [12] |
张珂, 姚小平. 土工格栅-粗粒土界面考虑尺寸效应直剪试验研究[J].
中国测试, 2021, 47(6): 51-56.
ZHANG K, YAO X P. Research on direct shear test of geogrid coarse grained soil interface considering effect of aperture ratio[J].
China Measurement & Test, 2021, 47(6): 51-56.
DOI:10.11857/j.issn.1674-5124.2021020065 |
| [13] |
荣笛, 孟陆波. 三轴循环荷载下饱和板岩的滞后特性研究[J].
中国测试, 2021, 47(6): 57-62.
RONG D, MENG L B. Study on hysteresis characteristics of saturated slate under triaxial cyclic load[J].
China Measurement & Test, 2021, 47(6): 57-62.
DOI:10.11857/j.issn.1674-5124.2020110036 |
| [14] |
JAVDANIAN H, JAFARIAN Y. Dynamic shear stiffness and damping ratio of marine calcareous and siliceous sands[J].
Geo-Mar Lett, 2018, 38: 315-322.
DOI:10.1007/s00367-018-0535-9 |
| [15] |
徐雪源, 徐玉中, 陈桂松, 等. 工业废料磷石膏的工程特性试验研究[J].
岩石力学与工程学报, 2004(12): 2096-2099.
XU X Y, XU Y Z, CHEN G S, et al. Testing study on engineering characteristics of phosphogypsum[J].
Chinese Journal of Rock Mechanics and Engineering, 2004(12): 2096-2099.
DOI:10.3321/j.issn:1000-6915.2004.12.028 |
| [16] |
HARDIN B O, DRNEVICH V P. Shear modulus and damping in soils: Design equations and curves[J].
ASCE Journal of the Soil Mechanics and Foundations Division, 1972, 98(SM7): 667-692.
|
| [17] |
庄心善, 赵汉文, 王俊翔, 等. 合肥膨胀土动弹性模量与阻尼比试验研究[J].
浙江大学学报(工学版), 2020, 54(4): 759-766.
ZHUANG X S, ZHAO H W, WANG J X, et al. Experimental study of dynamic elastic modulus and damping ratio of expansive soil in Hefei[J].
Journal of Zhejiang University(Engineering Science), 2020, 54(4): 759-766.
DOI:10.3785/j.issn.1008-973X.2020.04.015 |
| [18] |
DARENDELI M B. Development of a new family of normalized moduli reduction and material damping curves [D]. Austin: University of Texas at Austin, 2001.
|
| [19] |
谢定义. 土动力学[M]. 北京: 高等教育出版社, 2011: 141-149.
|
| [20] |
郜晋伟, 孟立新, 李小明, 等. 基于最小二乘圆拟合法的三轴转台垂直度误差测试[J].
中国测试, 2020, 46;(4): 123-129.
GAO J W, MENG L X, LI X M, et al. The verticality error test of three-axis turntable based on least square circle fitting method[J].
China Measurement & Test, 2020, 46;(4): 123-129.
DOI:10.11857/j.issn.1674-5124.2019090015 |
| [21] |
余湘娟, 吴克雄, 高磊. 某尾矿库坝基粉砂动力特性试验[J].
水利水运工程学报, 2016(2): 11-16.
XU X J, WU K X, GAO L. Experimental studies on dynamic characteristics of silty sand for tailing dam foundation[J].
Hydro-Science and Engineering, 2016(2): 11-16.
DOI:10.16198/j.cnki.1009-640X.2016.02.002 |
| [22] |
尹光志, 王文松, 魏作安, 等. 小打鹅尾矿库筑坝尾矿的动力学特性试验研究[J].
岩石力学与工程学报, 2017, 36(S1): 3121-3130.
YIN Z G, WANG W S, WEI Z A, et al. Experimental study on the dynamic characteristics of embankment tailings from Xiaodae tailings pond[J].
Chinese Journal of Rock Mechanics and Engineering, 2017, 36(S1): 3121-3130.
DOI:10.13722/j.cnki.jrme.2016.0177 |
 2024, Vol. 50
2024, Vol. 50