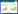文章信息
- 陈棣湘, 陈卓, 张琦, 潘孟春
- CHEN Dixiang, CHEN Zhuo, ZHANG Qi, PAN Mengchun
- 航空平台地磁矢量匹配导航算法研究进展
- Research progress on geomagnetic vector matching navigation algorithms for aviation platforms
- 中国测试, 2024, 50(5): 1-10
- CHINA MEASUREMENT & TEST, 2024, 50(5): 1-10
- http://dx.doi.org/10.11857/j.issn.1674-5124.2023110120
-
文章历史
- 收稿日期: 2023-11-29
- 收到修改稿日期: 2024-01-06
卫星导航技术由于具有精度高、无偏、无累积误差等优势,被广泛应用于航空平台的导航和定位。当前国际形势的不稳定性明显增加,一旦发生军事冲突,全球卫星导航系统(GNSS)易受干扰和攻击,会使航空平台在军事行动中很容易失去自主导航能力。因此,发展不依赖于GNSS的导航技术,并持续提升其可靠性和精度,具有重要的研究意义和战略价值。
目前,惯性导航是卫星导航的主要替代手段,但是惯性元件的零漂和累积误差导致其长时间使用时导航定位精度会不断下降。而航空平台一般都是在大范围、长航时的背景下执行任务,因此必须发展新型导航定位技术。
地磁场是地球的固有物理场,在地表与近地空间范围内,地理坐标与其对应的地磁信息之间存在着稳定的映射关系[1]。地磁导航是一种利用地磁数据库和真实路径磁测数据进行匹配的导航方式,由于它基本不受气候、环境等因素的影响,可有效提升航空平台的自主导航性能,因此当前世界各国对该技术的研究和应用也在日益深入。
现有的地磁导航主要采用总量匹配导航方式,分为相关匹配和滤波匹配两大类。其中相关匹配是将地磁测量数据与事先存储的地磁图进行相关运算,从而确定飞机在地磁图上的经纬度;当航空平台的飞行轨迹与地磁场总量等值线接近平行或者垂直时,地磁相关匹配的误匹配率很高。滤波匹配是将磁场测量数据和惯性导航系统的输出通过卡尔曼滤波器进行信息融合,通过不断递推寻找最优导航路径;地磁滤波匹配的结果受惯导误差特性影响较大,特别是当平台在地磁等值线上运动时,滤波结果会发散[2]。
由于地磁场是一个矢量场,地磁信息除了地磁总量外,还包含各个分量,因此地磁矢量导航与传统的地磁总量导航相比具有以下优势:1)信息量显著增加,可有效提高匹配成功率;2)当地磁总量相同时,其分量不一定相同,更有利于匹配。因此,综合利用地磁场各分量信息进行地磁矢量匹配,可以进一步提升地磁导航的精度,并使地磁导航技术具有更好的适用性[2-3]。
1 航空平台地磁矢量导航技术的发展 1.1 地磁矢量测量系统要实现高精度的地磁矢量导航,首先要获取高质量的地磁矢量测量数据,在此基础上构建出矢量地磁图。由于大范围内的地磁矢量测量难以在静止状态下完成,通常需要利用航空平台在飞行状态下实现动态测量。
2003年,澳大利亚基于稳定惯导平台研制了Falcon航空磁矢量测量系统,其基本组成如图1所示。该系统稳定平台上的陀螺仪等惯性仪器可以为飞机提供姿态信息,其定向精度约为0.003°。利用固定于机身的三轴磁通门传感器和惯性仪器的输出数据,可解算出地磁矢量。该系统的地磁矢量测量误差约为60 nT,已应用于西澳大利亚Rocklea条带状含铁地区的资源勘探和地质分析[4]。

|
| 图 1 Falcon航空地磁矢量测量系统搭载示意图 |
2013年,日本Honsho等[5]在Izu-Ogasawara岛开展了深海磁场矢量测量试验,其测量系统由三轴磁通门与环形激光陀螺仪构成,采用拖曳方式,在多航向多姿态情况下,均方根误差为20~30 nT。2017年,加拿大麦克马斯特大学的研究人员[6]研制了地面移动式地磁矢量测量系统,主要由三轴磁通门传感器、GPS和倾角仪等构成。经实验测定,其地磁矢量测量误差约30 nT。
2020年,捷克Hejda等[7]采用地磁台站与航空地磁矢量测量相结合的方式对磁异常场进行了观测,测量误差达到1 nT左右,但仅采用航空地磁矢量测量时,误差会增大一个量级以上。2022年,俄罗斯Aleshin等[8]基于无人机开展了区域航空磁测与磁图插值,通过与地磁台站观测数据对比,发现误差小于5%。国外典型地磁矢量测量系统的技术性能如表1所示。
| 国别 | 年份 | 测量方式 | 测量误差 |
| 澳大利亚 | 2003 | 飞机搭载,磁传感器和陀螺仪 | 60 nT |
| 日本 | 2013 | 飞机拖曳,磁传感器和陀螺仪 | 20~30 nT |
| 加拿大 | 2017 | 地面移动,三轴磁通门+GPS+倾角仪 | 约30 nT |
| 捷克 | 2020 | 地磁台站与航空磁测量结合 | 1 nT(单独测量>10 nT) |
| 俄罗斯 | 2022 | 无人机,航空地磁矢量测量 | 小于5% |
国内对基于航空平台的地磁矢量测量系统的研究相对较少。2018年,中国科学院国家空间中心王劲东等[9]研制了“萤火一号”卫星高精度磁强计,这是国内第一套用于空间磁场探测的高精度矢量磁力仪,在稳定的太空磁环境下测量分辨力可达到0.01 nT,但在地磁场环境下的测量性能还有待检验。2019-2021年,华中科技大学胡浪、缪林良、米洒洒等[10-12]先后开展了航空地磁探测实验,在磁传感器静态校正和航磁干扰补偿的基础上,地磁矢量测量精度约为20~30 nT。2020年,国家地震局地球物理研究所等单位[13-14]依托承担的国家重大科研项目,完成了海洋地磁场矢量测量仪功能样机的研制。该系统在磁屏蔽环境下的磁矢量测量分辨力达到0.01 nT,测量不确定度为0.2 nT,但未公布地磁开放环境下的测量结果。国内典型地磁矢量测量系统的技术性能如表2所示。
| 机构 | 年份 | 测量方式 | 技术性能 |
| 中国科学院 | 2018 | 卫星搭载,空间磁场探测 | 分辨力0.01 nT |
| 华中科技大学 | 2019-2021 | 航空地磁探测实验 | 精度20~30 nT |
| 国家地震局等单位 | 2020 | 磁屏蔽环境实验 | 分辨力0.01 nT,测量不确定度0.2 nT |
通过对地磁矢量测量系统发展状况的梳理可以发现,国外基于航空平台开展了较丰富的地磁矢量动态测量试验,而国内研究大部分还处于算法研究与原型机验证阶段。但是目前国内外的地磁矢量动态测量精度都还有限(误差约几十纳特斯拉),因此需要继续加强对磁传感器动态特性、磁传感器与姿态传感器的数据同步性、地磁动态测量数据处理方法等方面的研究,为地磁矢量测量误差的校正和补偿提供指导。
1.2 航空地磁导航系统2006年,美国Goodrich公司[15]设计了一套以E-2飞机为载体的地磁辅助导航系统,采用磁通门传感器测量地磁三分量,并将实时测量的地磁数据与事先存储的地磁图进行相关匹配,确定飞机的经纬度。通过飞行试验,发现1 h内的定位误差在600~1200 m之间。
2017年,美国空军技术学院Canciani等[16]采用光泵铯磁力仪、气压计和惯性导航系统,在较低的海拔高度和稳定的地磁环境下,利用高质量地磁图实现了13 m的定位精度。2020年7月,美国空军-麻省理工联合研究团队[17]在此基础上开展了进一步研究,仿真计算结果表明地磁导航的理论精度可以达到10 m。
2021年9月,美军将最新的地磁导航传感器和软件搭载在F-16飞机上,在内华达州爱德华兹空军基地试验场进行了航空地磁导航实验,在300 m高度下达到了59 m的定位精度[18]。
与国外相比,国内在地磁导航方面的研究大部分仍以算法研究[19-21]、仿真和小范围验证性实验为主[22-26],真正开展地磁导航外场试验的单位还不多。2009年,国防科技大学在湖南常德柳叶湖开展了水面地磁/惯性组合导航实验,获得了100 m的定位精度。2015年,哈尔滨工程大学设计了惯性/地形/地磁组合导航系统,并开展海上导航实验,航行了33 km,实验结果表明系统的纬度误差在500 m以内,经度误差在200 m以内[27]。2022年,国防科技大学智能传感与探测团队在海南博鳌地区基于塞斯纳飞机开展了航空地磁矢量动态测量和地磁矢量导航试验。试验结果表明,采用基于地磁二分量模式识别的匹配导航算法,在地磁特征较丰富(梯度>10 nT/km)区域的平均定位误差约为30 m,在地磁特征较贫瘠区域的平均定位误差约为39 m,这些试验结果与美军所报道的地磁导航精度水平基本相当[28]。国内外公开报道的典型地磁导航系统的技术性能如表3所示。
| 机构 | 年份 | 平台类型 | 定位精度/m |
| 美国Goodrich公司 | 2006 | E-2飞机 | 600~1200 |
| 美国空军技术学院 | 2017 | 直升机 | 13 |
| 美国空军 | 2021 | F-16飞机 | 59 |
| 哈尔滨工程大学 | 2015 | 船舶 | 200~500 |
| 国防科技大学 | 2022 | 塞斯纳飞机 | <39 |
2 航空地磁矢量导航算法研究进展
航空地磁矢量导航的关键技术主要包括地磁场三分量高精度测量、地磁矢量高精度解算、高精度高分辨率矢量地磁图构建、地磁矢量高精度高可靠性导航算法等。本文重点对航空地磁矢量导航算法近年来的研究进展进行评述。
地磁矢量导航算法是实现航空地磁矢量导航的核心,目前主流的地磁导航算法可分为递推滤波导航[29-30]和相关匹配导航[31-32]两大类。递推滤波需要以惯导提供的信息作为迭代的初始值,而强拒止环境下惯导的累积误差很容易导致算法发散;地磁矢量相关匹配是将地磁矢量信息基于一定准则映射到地磁图,通过相关性判断选择最优匹配结果。由于相关匹配算法受惯导累积误差的影响较小,因此更适用于航空地磁矢量导航。
地磁矢量相关匹配算法又可分为地磁轮廓线匹配(MAGCOM)和最近点迭代匹配(ICCP)两大类[33]。
2.1 基于MAGCOM的地磁矢量匹配算法当航空平台运动到地磁匹配区域时,磁传感器会按照一定的时间间隔测量得到匹配区域的地磁场值,并在经过干扰补偿后得到地磁场实测序列H = [h1,h2
当真实航迹与地磁等值线垂直或平行时,由于地磁场总量特征变化不明显,无法据此将惯导指示路径与真实路径区分开,导致MAGCOM算法易出现误匹配问题。由于地磁矢量信息比总量信息更丰富,采用基于MAGCOM的矢量匹配算法可以在很大程度上解决这一问题,其基本原理是:以惯导提供的参考轨迹作为初始匹配序列进行矢量相关匹配,通过相关性评价准则选择最优匹配结果,实现匹配定位。矢量相关匹配的相似度量采用均方差(MSD)最小准则,计算方法为:
| $ {\rm{m s d}}=\frac{1}{N} \sum_{k=1}^N\left(M_{S(i, j)}^k-M_M\right)^2 $ | (1) |
式中:
为了解决传统 MAGCOM 算法受运动平台航向误差影响较大的问题,文献[33]在传统平移搜索的基础上,增加了角度旋转搜索功能。该算法首先根据惯导参考轨迹提供的位置坐标计算航迹的重心,然后以重心为原点、以s为步长依次将参考航迹旋转一个角度a,再利用前述矢量相关匹配算法寻找最优偏角所对应的匹配结果。算法的基本流程如图2所示[33]。
|
| 图 2 基于MAGCOM的矢量匹配算法流程图 |
2.2 基于ICCP的地磁矢量匹配算法
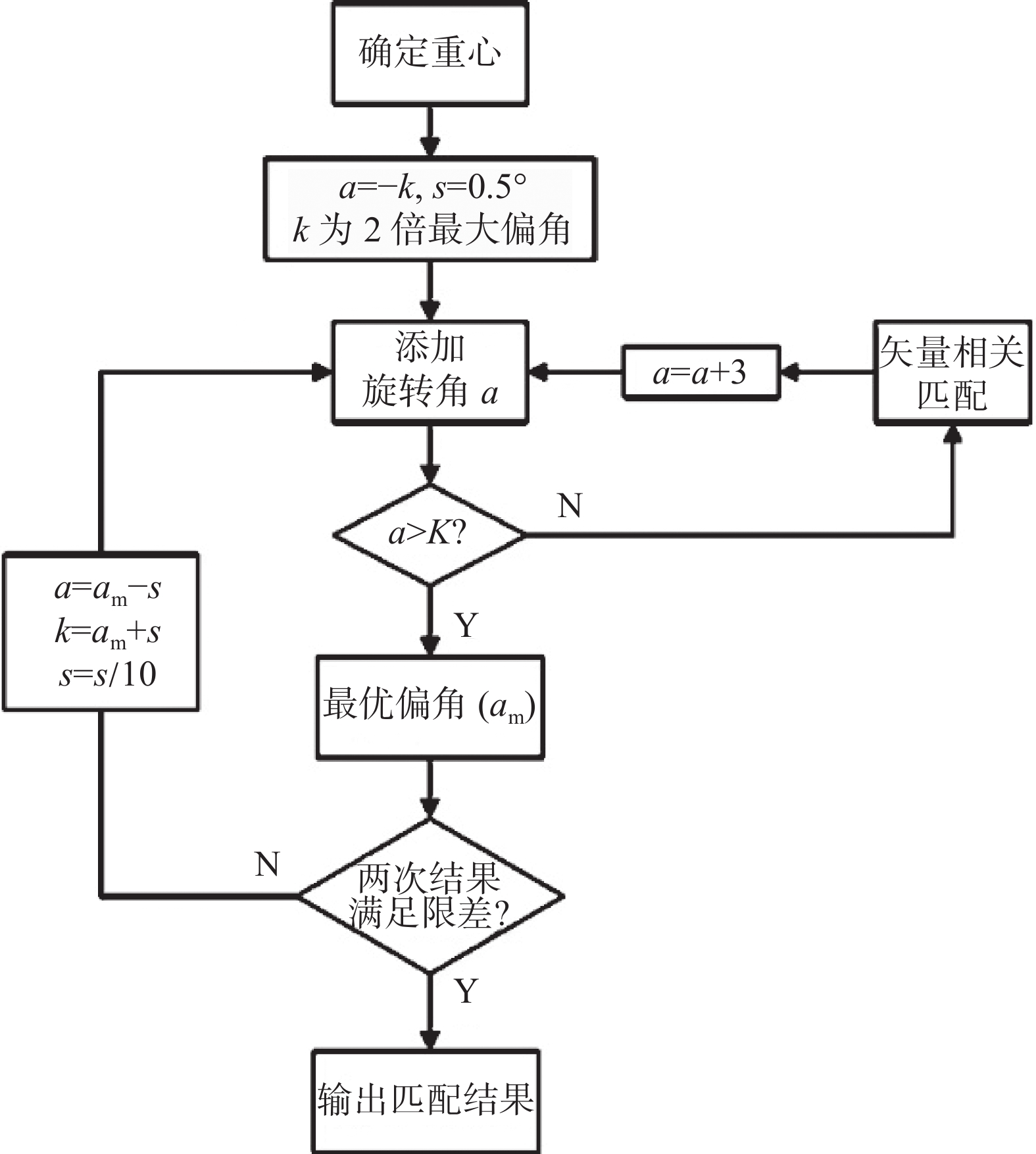
针对MAGCOM 算法易受航向误差影响的问题,研究人员通过借鉴图像匹配中ICP(iterative corresponding point)算法思路,提出了基于等值线的最近点迭代匹配算法(ICCP算法),其基本思想是根据载体运动路径上各磁测点之间的相对位置关系,使匹配点尽量位于与各点磁场测量值相对应的等值线上,该方法考虑了惯导航向误差和初始位置误差的影响[2]。
ICCP算法的基本原理如图3所示。图中ci(i=1,2
|
| 图 3 ICCP 算法原理示意图 |
若惯导初始误差太大,不满足惯导指示点位于地磁等值线附近这一条件,则ICCP算法容易出现发散;当真实航迹与地磁等值线平行或垂直时,由于根据磁场总量值难以区分惯导路径与真实路径,ICCP算法容易出现误匹配问题。针对这两点不足,考虑到地磁总量信息相同时各分量却往往有差异,文献[2]提出了基于ICCP的地磁矢量匹配算法,当在地磁等值线上寻找参考点时,不再采用坐标距离最近原则,而是根据地磁矢量的差异寻找参考点,这样就可以在很大程度上避免因地理坐标初始误差较大所引起的发散问题[2,33]。
基于ICCP的地磁矢量匹配算法在地磁图等值线上寻找与点hi距离最近的点gi时,地磁矢量的差异可用下式进行计算:
| $B_{\mathrm{d}}(j) = \sqrt{\left(B_{{\mathrm{t}} x}(j) - B_{{\mathrm{m}} x}\right)^2 + \left(B_{{\mathrm{t}} y}(j) - B_{{\mathrm{m}} y}\right)^2 + \left(B_{{\mathrm{t}} {\textit{z}}}(j)-B_{{\mathrm{m}} {\textit{z}}}\right)^2} $ | (2) |
式中:
由于ICCP算法与传统MAGCOM算法相比受航向误差的影响较小,因此基于ICCP原理的地磁导航算法对于航空平台更适用[2,36]。针对该算法在惯导初始误差较大时可能出现的发散问题,学者们尝试了多种改进方法。2019年,西北工业大学王琼等[37]将ICCP算法改进为三角形相关匹配,比基于单点信息的匹配具有更强的抗干扰性。2021年,南京航空航天大学付希禹等[38]采用等值线测点均方差粗匹配与ICCP滑动窗精匹配结合的方法,进一步提升了ICCP算法的精度。2022年,中国地质大学金子翔等[39]引入地磁梯度等值线的概念,通过梯度最近点迭代相关匹配与传统ICCP的结合共同计算定位点,将定位误差控制在半个网格之内,从而提升了ICCP算法在地磁变化平缓区域的匹配性能。2021年,美国安柏瑞德航空大学Cuenca等[40]提出了一种ICCP与扩展卡尔曼滤波融合的匹配导航算法,为GPS拒止情形下的航空平台提供了一种具有鲁棒性的导航方案。2023年,Cuenca等[41]利用粒子滤波器替代卡尔曼滤波器来优化ICCP算法,在航向误差相同的情况下,地磁匹配定位误差只有惯导定位误差的一半。
2.3 二分量地磁矢量导航算法2023年,国防科技大学陈卓[28]针对传统地磁矢量解算精度受惯导航向角累积误差影响的问题,提出了一种不依赖于航向角的二分量(地磁水平分量和垂向分量)地磁矢量导航方案,为航空平台地磁矢量匹配导航提供了一种新的思路。
如图4所示,被测地磁场

|
| 图 4 地磁二分量测量总体步骤 |
针对地磁特征贫瘠区域匹配算法易失效的问题,文献[28]设计了一种PNN-MLP(概率神经网络-多层感知机)级联的地磁二分量模式识别导航方法。该方法先对匹配区域的模式样本进行概率计算,通过第一级PNN网络粗筛出概率较大的样本路径,再将这些样本路径的地磁特征参数输入到第二级MLP网络进行精筛,从中筛选出最优路径。仿真和试验结果表明:在地磁特征贫瘠区域,基于级联神经网络的地磁匹配导航方法相比传统方法具有更好的鲁棒性[28]。
地磁二分量模式识别导航方法的基本原理如图5所示。假设航空平台上惯导提供的参考航迹为L,并于

|
| 图 5 模式识别地磁匹配导航原理示意图 |
如图6所示,PNN的输入层是各模式类序列和实测序列的地磁矢量数据(包含二分量与总量信息),PNN的输出层是匹配成功率大于98%的模式类路径;MLP的输入层是飞行路径上地磁二分量和总量的特征(地磁标准差、信息熵、平均梯度与最小梯度等),MLP的输出层为二分量和总量在各自子网络中的计算结果;最终在PNN-MLP的输出层通过标签分类,筛选出最优模式类对应的最优路径。

|
| 图 6 PNN-MLP级联的神经网络模型 |
2.4 其他地磁匹配导航算法
除了上述研究之外,近年来国内外学者们还将贝叶斯估计、卷积神经网络等引入到地磁匹配导航算法中,开展了一系列有益的探索,这些研究有力地促进了航空地磁矢量匹配导航技术的发展。
2017年,北京大学的刘岳峰等[42]提出了一种基于贝叶斯估计的地磁辅助导航算法,通过将匹配区域网格化,对匹配位置进行概率估计并实现定位,基于无人机实测地磁数据的仿真实验结果表明平均定位误差为89 m。
2019年,韩国科学技术高级研究院Kim等[43]提出了一种卷积神经网络和归一化互相关结合的地磁匹配导航方法,利用两个对称的CNN网络在搜索区域内缩小匹配范围,进而利用互相关匹配寻找最佳导航路径,仿真结果表明匹配成功率可达98.6%以上。
2020年,法国格勒诺布尔实验室Abid等[44]利用卷积神经网络开发了室内定位系统,采用递归图(recurrent plots, RPs)作为序列信息进行匹配,实验测试发现匹配准确率达到95.46%以上。
2022年,美国安柏瑞德航空大学Cuenca等[45]开展了用机器学习技术提升位置估计精度的研究,并提出可通过增加其他地磁相关特征参数来提升神经网络训练效果。
3 后续研究方向航空平台地磁矢量导航涉及的研究领域广、关键问题多,目前仍有许多问题亟待进一步解决,包括磁传感器动态误差补偿、捷联式地磁矢量导航系统的数据同步、矢量磁场延拓、高性能地磁导航算法等;就航空平台地磁矢量匹配导航算法而言,可重点从以下4个方面进行改进:
1)进一步提升算法的鲁棒性和精度
现有的地磁匹配导航算法(如MAGCOM算法、ICCP算法)在真实航迹与地磁等值线垂直或平行时,由于地磁场总量特征不明显,都难以取得非常理想的匹配效果;基于地磁矢量信息的匹配导航算法虽然可以在一定程度上解决这一问题,但航空平台长航时飞行情况下惯导的累积误差会导致其输出的参考路径位置误差较大,使算法出现发散或无法满足导航定位的精度要求。针对此问题,可在充分利用地磁总量和三分量信息的基础上,进一步研究基于地磁梯度、磁偏角、磁倾角等不同地磁特征的最优路径判别方法,从而提升匹配导航算法的鲁棒性和精度。
2)大力发展基于机器学习的地磁矢量匹配导航方法
基于相关匹配的传统地磁导航方法对磁测数据和磁图数据的要求较高,在地磁特征贫瘠情况下匹配性能会明显下降。由于地磁矢量数据与地理位置之间的映射关系难以通过相关性来完整描述,采用机器学习方法对海量地磁矢量数据及其特征参数进行分类、识别,建立与地理位置的非线性映射关系,是极具发展潜力的一种方式。未来应当充分利用地磁矢量信息丰富的特点,研究基于不同输入参数、不同神经网络结构的地磁矢量匹配导航算法,并引入深度学习算法(如改进卷积神经网络、循环神经网络等模型)来提高数据处理速度和准确度。
3)推动无人机等新型航空平台地磁矢量导航技术发展
无人机作为新型航空平台,由于具有灵活性强、成本低等优势,在民用和军事领域的应用都越来越广泛。将地磁矢量导航技术应用于无人机上,可进一步增强其抗干扰性能,扩展其生存能力。但由于无人机可搭载的载荷有限,对地磁矢量导航系统的体积、质量和功耗等指标都有更苛刻的要求,相应的地磁矢量匹配导航算法也要考虑无人机与大型飞机在机动性、飞行速度和飞行范围等方面的差别。
4)加强试验研究
目前,美军已在主力战机上进行了航空地磁导航试验。相比之下,国内的航空地磁导航应用研究滞后。试验研究对于方法验证和改进具有巨大提升效应。通过开展大量相关试验,可获取更丰富的地磁矢量数据,通过从地磁矢量测量到矢量地磁图构建,再到地磁矢量导航算法的反复迭代验证,最终可构建一套完整的航空地磁矢量导航技术体系和手段。
4 结束语航空地磁矢量导航技术在军事和民用领域均具有很高的战略意义和应用价值。本文对航空平台地磁矢量导航技术的发展过程进行了系统的梳理,重点对地磁矢量匹配导航算法近年来的研究进展进行了分析和评价,并指出了未来的研究重点和发展方向。期待有更多同行关注这一领域,推动该技术的进一步发展。
| [1] |
翁利斌, 张添翼, 王握文. 地磁导航: 地球母亲的“金手指”[J].
科学中国人, 2020(19): 78-79.
WENG L B, ZHANG T Y, WANG W W. Geomagnetic navigation: The "golden finger" of mother earth[J].
Sci-Tech Expo, 2020(19): 78-79.
|
| [2] |
吴凤贺, 张琦, 潘孟春, 等. 基于ICCP的地磁矢量匹配算法研究[J].
中国测试, 2018, 44(2): 103-107.
WU F H, ZHANG Q, PAN M C, et al. Study on geomagnetic vector matching algorithm based on ICCP[J].
China Measurement & Test, 2018, 44(2): 103-107.
DOI:10.11857/j.issn.1674-5124.2018.02.021 |
| [3] |
YUAN R, LIHUI W, KUNJIE L, et al. Improved iterative closest contour point matching navigation algorithm based on geomagnetic vector[J].
Electronics, 2022, 11(796): 796.
|
| [4] |
DRANSFIELD M, CHRISTENSEN A, LIU G. Airborne vector magnetics mapping of remanetly magnetized banded iron formations at rocklea, western Australia[J].
Exploration Geophysics, 2003, 34(1): 93-96.
|
| [5] |
HONSHO C, URA T, KIM K. Deep-sea magnetic vector anomalies over the hakurei hydrothermal field and the bayonnaise knoll caldera, Izu-Ogasawara Arc, Japan[J] Journal of Geophysical Research: Solid Earth, 2013, 118(10): 5147-5164.
|
| [6] |
INOZEMTSEV I. Land-based vector magnetic survey of a bif-hosted iron ore deposit, MARY River, BAFFIN Island, Nunavut[D]. Canada: McMaster University, 2017.
|
| [7] |
HEJDA P, ČÁPOVÁ D, HUDEČKOVÁ E, et al. Analysis of the czech magnetic anomaly data obtained by ground-based and airborne magnetic surveys[C]//EGU General Assembly Conference Abstracts, 2020.
|
| [8] |
ALESHIN I, KHOLODKOV K, MALYGIN I, et al. Geomagnetic survey interpolation with the machine learning approach[J].
arXiv preprint, 2022(2210): 3379-3383.
|
| [9] |
王劲东, 薛洪波, 张艺腾, 等. 高精度航空地磁矢量测量技术[C]//2018年中国地球科学联合学术年会, 2018.
WANG J D, XUE H B, ZHANG Y T, et al. High precision aerial geomagnetic vector measurement technology[C]//2018 China Earth Science Joint Academic Annual Conference, 2018.
|
| [10] |
胡浪. 航空地磁探测中地磁矢量测量误差补偿算法研究[D]. 武汉: 华中科技大学, 2019.
HU L. Research on geomagnetic vector measurement error compensation algorithm in aeromagnetic geomagnetic detection[D]. Wuhan: Huazhong University of Science & Technology, 2019.
|
| [11] |
缪林良, 米洒洒, 王玮琳, 等. 航磁矢量测量的误差分析和补偿算法研究[J].
电子测量与仪器学报, 2021, 35(12): 15-23.
MIAO L L, MI S S, WANG W L, et al. Error analysis and compensation algorithm research of aeromagnetic vector measurement[J].
Journal of Electronic Measurement and Instrumentation, 2021, 35(12): 15-23.
|
| [12] |
米洒洒. 面向直升机地磁测量系统的航磁补偿算法研究[D]. 武汉: 华中科技大学, 2021.
MI S S. Research on aeromagnetic compensation algorithm for helicopter geomagnetic survey system[D]. Wuhan: Huazhong University of Science & Technology, 2021.
|
| [13] |
蔡建平, 廖佳华, 陈洁, 等. 海洋地磁场矢量测量仪支撑装置结构设计与有限元分析[J].
机械设计, 2020, 37(7): 124-131.
CAI J P, LIAO J H, CHEN J, et al. Structural design and finite element analysis of supporting device for marine geomagnetic field vector measuring instrument[J].
Journal of Machine Design, 2020, 37(7): 124-131.
|
| [14] |
王喆. 海洋地球磁场矢量测量系统关键技术研究[D]. 北京: 中国地震局地球物理研究所, 2020.
WANG Z. Research on key technologies of marine geomagnetic field vector measurement system[D]. Beijing: Institute of Geophysics, China Earthquake Administration, 2020.
|
| [15] |
GOLDENBERG F. Geomagnetic navigation beyond the magnetic compass[C]//Proceedings of IEEE/ION PLANS, 2006.
|
| [16] |
CANCIANI A, RAQUET J. Airborne magnetic anomaly navigation[J].
IEEE Transactions on Aerospace & Electronic Systems, 2017(53): 67-80.
|
| [17] |
GNADT R, BELARGE J, CANCIANI A, et al. Signal enhancement for magnetic navigation challenge problem[J]. 2020(7): 315-327.
|
| [18] |
AARON C. Magnetic navigation on an F-16 aircraft using online calibration[J].
IEEE Transactions on Aerospace and Electronic Systems, 2022(58): 420-434.
|
| [19] |
王立辉, 许宁徽, 刘庆雅. 基于粒子约束的粒子群地磁匹配算法[J].
中国惯性技术学报, 2020, 28(6): 755-760.
WANG L H, XU N H, LIU Q Y. A PSO geomagnetic matching algorithm based on particle constraint[J].
Journal of Chinese Inertial Technology, 2020, 28(6): 755-760.
|
| [20] |
田哲旭. 基于向量搜索的地磁导航匹配算法研究[J].
新型工业化, 2022(12): 5-8.
TIAN Z X. Research on geomagnetic navigation matching algorithm based on vector search[J].
New Industrialization, 2022(12): 5-8.
|
| [21] |
邓小波, 赵军瑞, 宋胜. 基于地磁方向熵的高空地磁匹配航迹选取方法[J].
无线电工程, 2022(52): 840-845.
DEGN X B, ZHAO J R, SONG S. High altitude geomagnetic matching track selection method based on geomagnetic direction entropy[J].
Radio Engineering, 2022(52): 840-845.
DOI:10.3969/j.issn.1003-3106.2022.05.019 |
| [22] |
欧超. 惯性/地磁组合导航方法研究[D]. 哈尔滨: 哈尔滨工业大学, 2020.
OU C. Research on inertial/geomagnetic navigation method[D]. Harbin: Harbin Institute of Technology, 2020.
|
| [23] |
保金宏. 基于地磁匹配的组合导航技术研究[D]. 杭州: 杭州电子科技大学, 2020.
BAO J H. Research on integrated navigation technology based on geomagnetic matching[D]. Hangzhou: Hangzhou Dianzi University, 2020.
|
| [24] |
王立辉, 刘庆雅. 飞行器编队PSO多维地磁匹配算法[J].
电光与控制, 2021, 28(3): 41-45.
WANG L H, LIU Q Y. Multi-dimensional PSO geomagnetic matching algorithm for aircraft formation[J].
Electronics Optics & Control, 2021, 28(3): 41-45.
DOI:10.3969/j.issn.1671-637X.2021.03.008 |
| [25] |
孙建港, 周诗超, 刘威, 等. 基于地磁匹配技术的室内定位系统设计[J].
传感器与微系统, 2022(41): 97-100.
SUN J G, ZHOU S C, LIU W, et al. Design of indoor positioning system based on geomagnetic matching technology[J].
Transducer and Microsystem Technologies, 2022(41): 97-100.
|
| [26] |
赵琴, 徐卿, 齐静雅, 等. 基于天文/地磁组合的临近空间自主导航系统研究[C]//第十三届中国卫星导航年会, 2022.
ZHAO Q, XU Q, QI J Y, et al. The autonomous navigation system in near space based on astronomic/geomagnetic combination[C]//The 13th Annual Meeting of China Satellite Navigation, 2022.
|
| [27] |
马妍. 水下运载器惯性/地形/地磁组合导航系统关键技术研究[D]. 哈尔滨: 哈尔滨工程大学, 2015.
MA Y. Research on key technologies of INS/TAN/GAN integrated navigation system for underwater vehicles[D]. Harbin: Harbin Engineering University, 2015.
|
| [28] |
陈卓. 面向航空平台的地磁矢量导航关键技术研究[D]. 长沙: 国防科技大学, 2023.
CHEN Z. Research on key technologies of geomagnetic vector navigation for aeronautical platforms[D]. Changsha: National University of Defense Technology, 2023.
|
| [29] |
王向磊, 田颜锋. 基于地磁场的自主导航研究[J].
地球物理学报, 2010(53): 2724-2730.
WANG X L, TIAN Y F. Autonomous navigation based geomagnetic research[J].
Chinese Journal of Geophysics, 2010(53): 2724-2730.
|
| [30] |
栾禄雨, 葛德宏, 陈建华. 基于多参量信息的水下地磁滤波导航算法[J].
导航与控制, 2015(14): 80-83.
LUAN L Y, GE D H, CHEN J H. Geomagnetic navigation algoriths based on multi-parameter information[J].
Navigation and Control, 2015(14): 80-83.
DOI:10.3969/j.issn.1674-5558.2015.05.014 |
| [31] |
XIE W, QU Z, LI Q. A fast algorithm of the geomagnetic correlation matching based on MSD[C]//Proceedings of Third International Conference on Control, Automation and Systems Engineering(CASE), 2013.
|
| [32] |
徐晓苏, 吴剑飞, 徐胜保, 等. 基于仿射修正技术的水下地形ICCP匹配算法[J].
中国惯性技术学报, 2014(22): 362-367.
XU X S, WU J F, XU S B, et al. ICCP algorithm for underwater terrain matching navigation based on affine correction[J].
Journal of Chinese Inertial Technology, 2014(22): 362-367.
|
| [33] |
吴凤贺. 地磁矢量匹配导航技术研究[D]. 长沙: 国防科技大学, 2017.
WU F H. Study on geomagnetic vector matching navigation technology[D]. Changsha: National University of Defense Technology, 2017.
|
| [34] |
朱文奇. 高性能地磁匹配导航算法的研究[D]. 西安: 西安理工大学, 2016.
ZHU W Q. Study on the high-performance of geomagnetic matching navigation algorithm[D]. Xi'an: Xi'an University of Technology, 2016.
|
| [35] |
刘亚云. 地磁匹配导航算法及地磁场模拟系统研究[D]. 哈尔滨: 哈尔滨工业大学, 2011.
LIU Y Y. Research on thegeomagnetic navigation matching algorithm and the geomagnetic field simulation system[D]. Harbin: Harbin Institute of Technology, 2011.
|
| [36] |
CHEN K, LIANG W, LIU M, et al. Comparison of geomagnetic aided navigation algorithms for hypersonic vehicles[J].
Journal of Zhejiang University Science A (Applied Physics & Engineering), 2020, 21(8): 673-683.
|
| [37] |
WANG Q, ZHOU J. Triangle matching method for the sparse environment of geomagnetic information[J].
Optik, 2019(181): 651-658.
|
| [38] |
付希禹, 孙永荣, 李荣冰. 基于 MSD 和 ICCP 改进的地磁联合匹配算法[J].
南京航空航天大学学报, 2021(53): 928-933.
FU X Y, SUN Y R, LI R B. Improved geomagnetic united matching algorithm based on MSD and ICCP[J].
Journal of Nanjing University of Aeronautics & Astronautics, 2021(53): 928-933.
|
| [39] |
金子翔, 许苏鹏, 张贵宾, 等. 一种适用于地磁梯度匹配导航的 ISCCP 算法[J].
物探与化探, 2022(46): 1225-1231.
JIN Z X, XU S P, ZHANG G B, et al. An ISCCP algorithm for geomagnetic gradient matching for navigation[J].
Geophysical & Geochemical Exploration, 2022(46): 1225-1231.
|
| [40] |
CUENCA A, MONCAYO H. A geomagnetic-based integrated architecture for dead-reckoning navigation[C]//AIAA Scitech 2021 Forum, 2021.
|
| [41] |
CUENCA A, MONCAYO H. Geomagnetic aided navigation using rao blackwellized particle filter[C]//AIAA Scitech 2023 Forum, 2023.
|
| [42] |
刘岳峰, 郑培晨. 一种基于贝叶斯估计的地磁辅助惯性导航算法[J].
北京大学学报(自然科学版), 2017(53): 873-880.
LIU Y F, ZHENG P C. A Bayesian estimation-based algorithm for geomagnetic aided inertial navigation[J].
Acta Scientiarum Naturalium Universitatis Pekinensis, 2017(53): 873-880.
|
| [43] |
KIM D, BANG H, LEE C. Approach to geomagnetic matching for navigation based on a convolutional neural network and normalised cross-correlation[J]. IET Radar, Sonar & Navigation, 2019 (13): 1323-1332.
|
| [44] |
ABID M, LEFEBVRE G. Improving indoor geomagnetic field fingerprinting using recurrence plot-based convolutional neural networks[J].
Journal of Location Based Services, 2021, 15(1): 61-87.
DOI:10.1080/17489725.2020.1856428 |
| [45] |
CUENCA A, MONCAYO H. Machine learning application to estimation of magnetospheric contributions for geomagnetic-based navigation[C]// AIAA Scitech 2022 Forum, 2022.
|
 2024, Vol. 50
2024, Vol. 50