文章信息
- 李华洋, 曹志鹏, 吴小龙, 朱施杰, 邓金根, 张水良
- LI Huayang, CAO Zhipeng, WU Xiaolong, ZHU Shijie, DENG Jin’gen, ZHANG Shuiliang
- 基于LightGBM算法的地层破裂压力预测方法及应用
- Prediction method of formation fracture pressure based on LightGBM algorithm and its application
- 中国测试, 2024, 50(4): 134-143
- CHINA MEASUREMENT & TEST, 2024, 50(4): 134-143
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022120017
-
文章历史
- 收稿日期: 2022-12-04
- 收到修改稿日期: 2023-02-18
2. 中国石油大学(北京) 油气资源与探测国家重点实验室,北京 102249;
3. 中国科学院武汉岩土力学研究所 岩土力学与工程国家重点实验室,湖北 武汉 430071;
4. 重庆大学 煤矿灾害动力学与控制国家重点实验室,重庆 400044;
5. 中海油天津分公司,天津 300459
2. State Key Laboratory of Petroleum Resource & Prospecting, China University of Petroleum (Beijing), Beijing 102249, China;
3. State Key Laboratory of Geomechanics and Geotechnical Engineering, Institute of Rock and Soil Mechanics, Chinese Academy of Science, Wuhan 430071, China;
4. State Key Laboratory of Coal Mine Disaster Dynamics and Control, Chongqing University, Chongqing 400044, China;
5. CNOOC Tianjin Branch, Tianjin 300459, China
2021年中国的原油进口量高达5.13亿吨,对外依存度为72%,天然气进口量为1680亿立方米,较2020年增长19.9%,我国对油气资源的需求量与日俱增。随着浅部油气资源的开发殆尽,石油工业向深层、超深层进军已经是大势所趋。作为国内石油资源的重要接力产区,吐哈油田和塔里木油田超过73%的油气资源埋深达5000 m以下。由于深层、超深层的地质环境和纵向岩性剖面复杂,且深部地层往往存在异常高压[1],导致钻井过程中井壁失稳现象频发,深层油气资源的勘探开发及其所带来的一系列技术难题的攻关已经是刻不容缓。
地层破裂压力是指使地层产生裂缝时的流体压力。作为影响井壁稳定性的重要数据,破裂压力一直是地层各压力监测的重点内容。岩石本身的性质是影响地层破裂压力的最重要的部分,其主要影响因素包括井壁岩石弹性系数、裂缝发育程度和地层抗拉伸强度。对于钻井施工而言,对地层破裂压力当量密度进行精确预测可以有效地防止泄漏、井喷、塌陷、卡钻等井下事故的发生,是确定安全泥浆密度窗口、规划套管方案及压裂增产措施的重要依据。
破裂压力的研究始于二十世纪五十年代。1957年,哈伯特(Hubbert)和威利斯(Willis)在研究水力压裂的过程中提出了著名的H-W模型,这也是第一个计算破裂压力的公式模型[2]。计算地层破裂压力的方法有很多,不同方法的适用条件也不同。目前常用的传统计算破裂压力的方法有:伊顿法[3]、STEPHEN法[4]和黄荣樽法[5]。上述方法可简单分为两大类,一类是比较经典的理论公式法,这也是实验室计算所常用的,主要包括Eaton法、“六五”、“七五”模型、Holbrook法;另一类就是现场常用的利用地质参数进行预测的方法,主要有Anderson法、现场施工参数法、测井资料法、声波测井法以及CYT(空间源直接探矿仪)资料法等。尽管哈伯特(Hubbert)、马休斯(Matthews)、伊顿(Eaton)等人接连构建出地层破裂压力的计算模型,这些方法也都简单可行,在我国的油气勘探领域得到广泛的应用,但是都存在一定的局限性。例如,伊顿法实际上是一个建立在北美墨西哥湾地区的经验公式,仅适用于地层沉积新、构造运动少的连续沉积盆地[6]。上述方法在实际计算过程中往往不能直接套用公式,而是需要结合目标区块的地质环境等条件,优选计算模型并对模型进行修正。故上述预测公式不具备普遍意义。
近些年来,机器学习在石油行业有着广泛的应用,如油井产量预测[7]、地层复杂岩性识别[8]、地层孔隙压力预测[9]等。针对传统地层破裂压力预测方法中存在的适用条件单一、适用范围狭小、普适性不高、严重依赖油田现场地漏试验数据等问题,本文提出了一种基于LightGBM机器学习算法的地层破裂压力预测新方法。以S区块的3口直井为例验证了LightGBM模型的准确性并与传统的声波测井资料法进行比对分析。
1 理论与方法本文介绍了声波测井资料法这种传统的破裂压力预测方法,该方法是实验室和油田现场常用的计算方法,同时介绍本文建立的破裂压力智能预测模型所采用的LightGBM机器学习算法。
1.1 声波测井资料法声波(通常为纵波)的传播速度只与弹性岩石的密度、泊松比、动态弹性模量相关。所以若可以测量岩石中纵波和横波的时差和密度,就可以求得岩石的泊松比和动态弹性模量。截至目前,破裂压力的预测直接采用岩石的动态弹性参数,而静态参数一般由动态参数经验转换。
根据测井得到的地层密度和声波时差等数据,计算地层泊松比、构造应力系数、Biot有效应力贡献系数等参数,得到破裂压力。中国石油大学(北京)、江汉石油学院(现长江大学)、华北油田共同提出了一套利用声波测井数据预测地层破裂压力的模型[10],如下:
| $ {P}_{\mathrm{f}}=\frac{{\xi }_{1}E_{\mathrm{s}}}{\left(1-\mu \right)}-\frac{2{\xi }_{2}E_{\mathrm{s}}}{\left(1+\mu \right)}+\frac{2\mu \left(S-\alpha {P}_{\mathrm{p}}\right)}{\left(1-\mu \right)}+\alpha {P}_{\mathrm{p}}+{S}_{{\mathrm{t}}} $ | (1) |
式中:Pf——破裂压力,MPa;
ξ1、ξ2——水平方向上的两个构造应力系数;
Es——静态弹性模量,MPa;
μ——地层岩石泊松比(静态),无因次量;
Pp——地层孔隙压力,MPa;
S——地静压力,MPa;
St——岩石抗拉伸强度,MPa;
α——毕奥特(Biot)系数,代表地层孔隙压力对颗粒间压力的影响。
该模型综合了岩石静态泊松比和弹性模量对地层破裂压力的作用。如果地下岩体中没有构造应力,仅受到由岩体质量产生的水平应变所约束的侧向力,此时可将ξ1、ξ2当作零。
该公式中,除了地层孔隙压力采取伊顿法(Eaton)法计算外,其余变量均根据声波测井资料求得。该公式基于地层中作用于水平主方向上的两个不等主应力,考虑了井壁岩石的弹性系数、Biot系数和抗拉强度等影响因素,计算结果误差较小。此外,在计算过程中,直接用岩石动态参数计算地层破裂压力一般误差稍大,故为减小计算误差,一般采用经验公式继续计算静态岩石参数。
1.2 LightGBM算法LightGBM算法(轻量级梯度提升机算法)是一种高效梯度提升决策树算法[11]。LightGBM算法起源于微软亚洲研究院在神经信息处理系统进展大会(NIPS)发表的系列论文,它是对GBDT(梯度提升决策树)算法的改进,即改善了GBDT在准确率和效率方面的问题,在不降低预测精度情况下,减少训练时间,大大降低了内存的占用。“Light”意为轻量级,其主要体现在三个方面,即样本、特征、内存均减小[12]。
LightGBM算法主要采用如下4种方式提升训练速度降低误差:
1)单边梯度采样法(gradient based one side sampling, GOSS)。GOSS是从样本中选取有较大梯度的数据以此来提升准确率,排除大部分小梯度的样本,只用剩下的样本计算信息增益。梯度大的实例对信息增益有更大的影响,所以保留梯度较大的样本,去掉梯度较小的样本。具体步骤为:若大梯度样本为a×100%,则小梯度样本为(1–a)×100%,然后再从小梯度样本中随机取b×100%,则取得总样本为b(1–a)×100%。最后,GOSS通过将采样数据按照较小梯度数据乘以权重系数(1–a)/b来计算信息收益,其中a、b∈(0,1)。具体关系如图1所示。
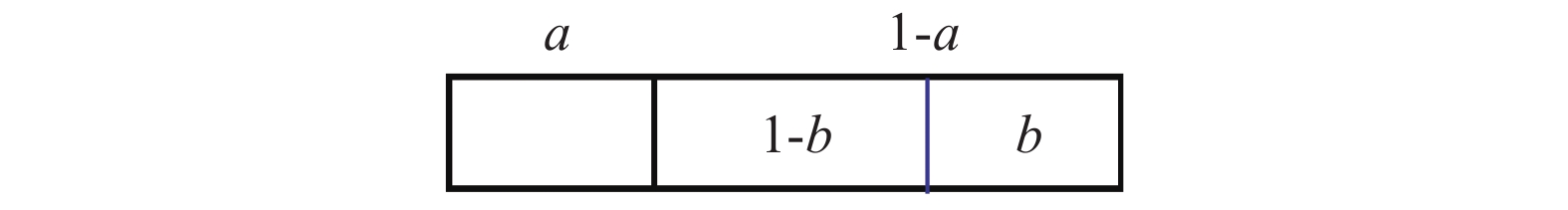
|
| 图 1 GOSS算法数据关系图 |
2)互斥特征捆绑法(exclusive feature bundling, EFB)。EFB可以捆绑互斥特征,使其同时取非零值,也就是用一个合成特征来取代它。在实际应用中,虽然特征量比较多,但是由于特征空间十分稀疏,所以EFB可以将数据的部分特征进行合并从而降低数据维度。
3)基于Histogram的决策树算法。一个叶子节点可以由其父节点和兄弟节点做差得到,在运算速度上可以得到显著提升[13]。在模型训练过程中,将每个连续的特征数据进行分段处理,样本中对应该段的取值会被放到一起,最终会将一系列连续的特征值通过分裂点分成离散值。所以利用Histogram算法将不会完全遍历所有数据而是只需要遍历所有分裂点找到最佳分裂点即可。
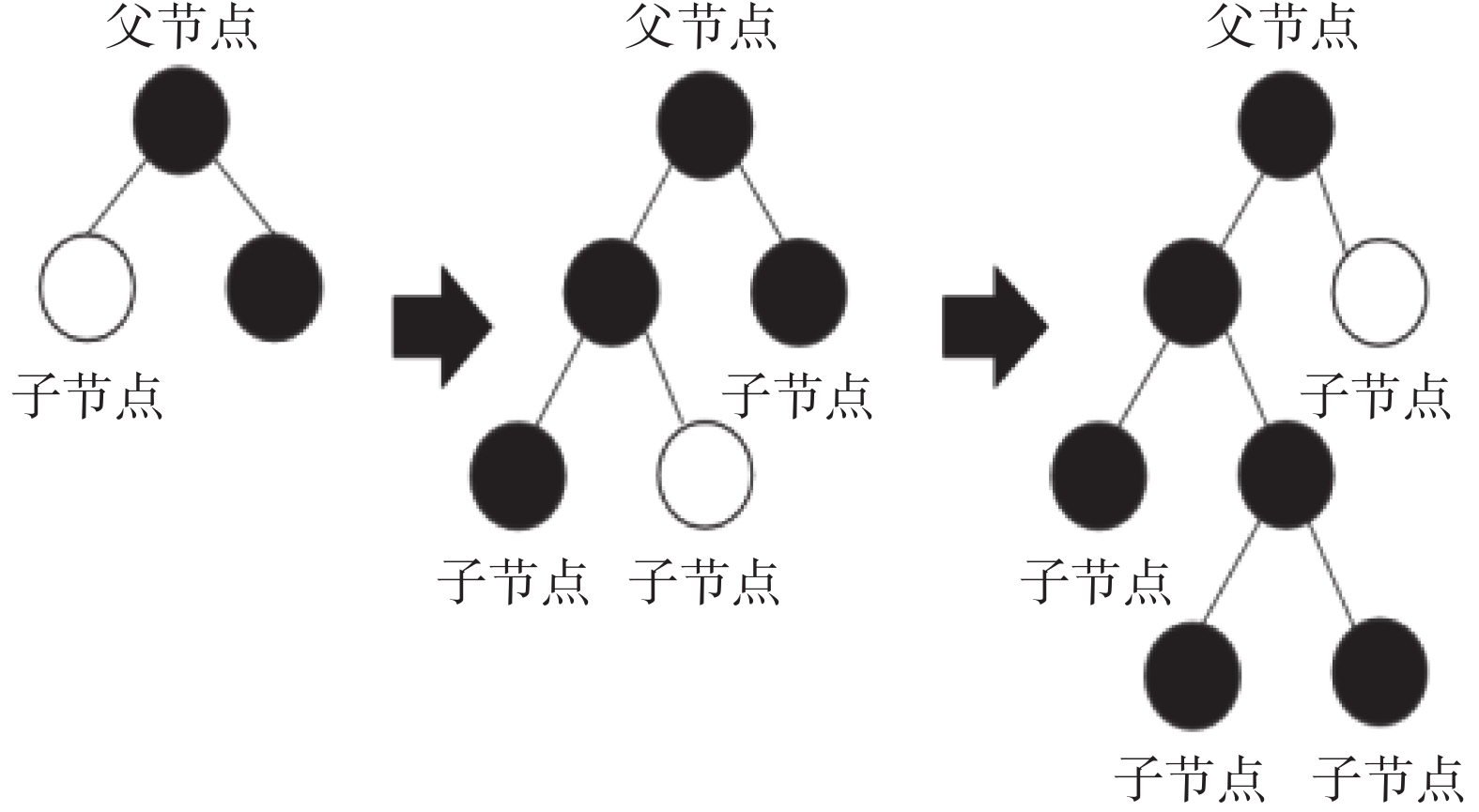
4)带深度限制的Leaf-wise 叶子生长策略。GBDT算法使用的是按层生长的决策树生长策略,而且由于不加区分地对待同一层的叶子,会带来很多额外的开销。实际上很多叶子的分裂增益很低,这就带来了低收益的额外开销。LightGBM则使用了带有深度限制的Leaf-wise生长策略,在分裂次数相同的情况下,Leaf-wise可以在降低误差的同时,得到更好的精度效果(Leaf-wise的算法原理如图2)。考虑到地层中可能存在的异常地层压力问题,容易在模型训练过程中存在过拟合问题,所以采用限制最大深度的策略,可以在保证高效的同时,预防过拟合情况的发生。
|
| 图 2 带深度限制的Leaf-wise生长策略 |
LightGBM算法相较于传统的GBDT算法,保证了预测精度,减少了训练时间,降低了内存占用,既能防止模型的过拟合,又能保证模型的高性能。
2 破裂压力预测模型的构建 2.1 训练样本的选择本文的研究数据来自S区块的3口直井,分别为S-1井、S-2井和S-3井。由于该区块经历过多期构造运动,导致该区块内部构造样式复杂,深部断层发育,浅部泥岩易水化,中深部硬脆性泥岩容易发生井壁坍塌,造成漏、喷、塌、卡等复杂问题。该区块压力系统复杂,且作为新探区各种地质和测井资料缺失严重,传统的地层各压力预测方法难以满足工程需要。
地层某处的岩石是否产生破裂其主要的影响因素可分为两类,一类是地层岩石本身的性质,如岩石的泊松比和抗拉强度等[14]。另一类是地层的某些压力,如孔隙压力和上覆岩层压力等[15]。建立破裂压力智能预测模型的重要基础在于合理地选择输入层数据,这直接关系到模型的预测精度。选择的标准在于输入层数据既要与输出层数据(即破裂压力当量密度)有直接关联,又要确保数据的连续性,数据要容易获取。岩石的泊松比和抗拉强度均是通过取岩心进行室内岩石力学实验获得,泊松比可通过单轴抗压试验获得,而巴西劈裂法是目前测定岩石抗拉强度的主要方法。通过岩石力学实验获取的参数均为离散数据,不具备连续性,并且室内岩石力学实验操作复杂,费用昂贵,不适合作为预测模型的输入层数据。上覆岩层压力的决定因素在于井深和地层密度,而地层密度可通过测井资料获取。地层孔隙压力也可以通过测井资料计算得到。故本文采用机器学习方法,基于LightGBM算法,以井深、孔隙压力当量密度和地层密度作为输入层,预测地层破裂压力当量密度。
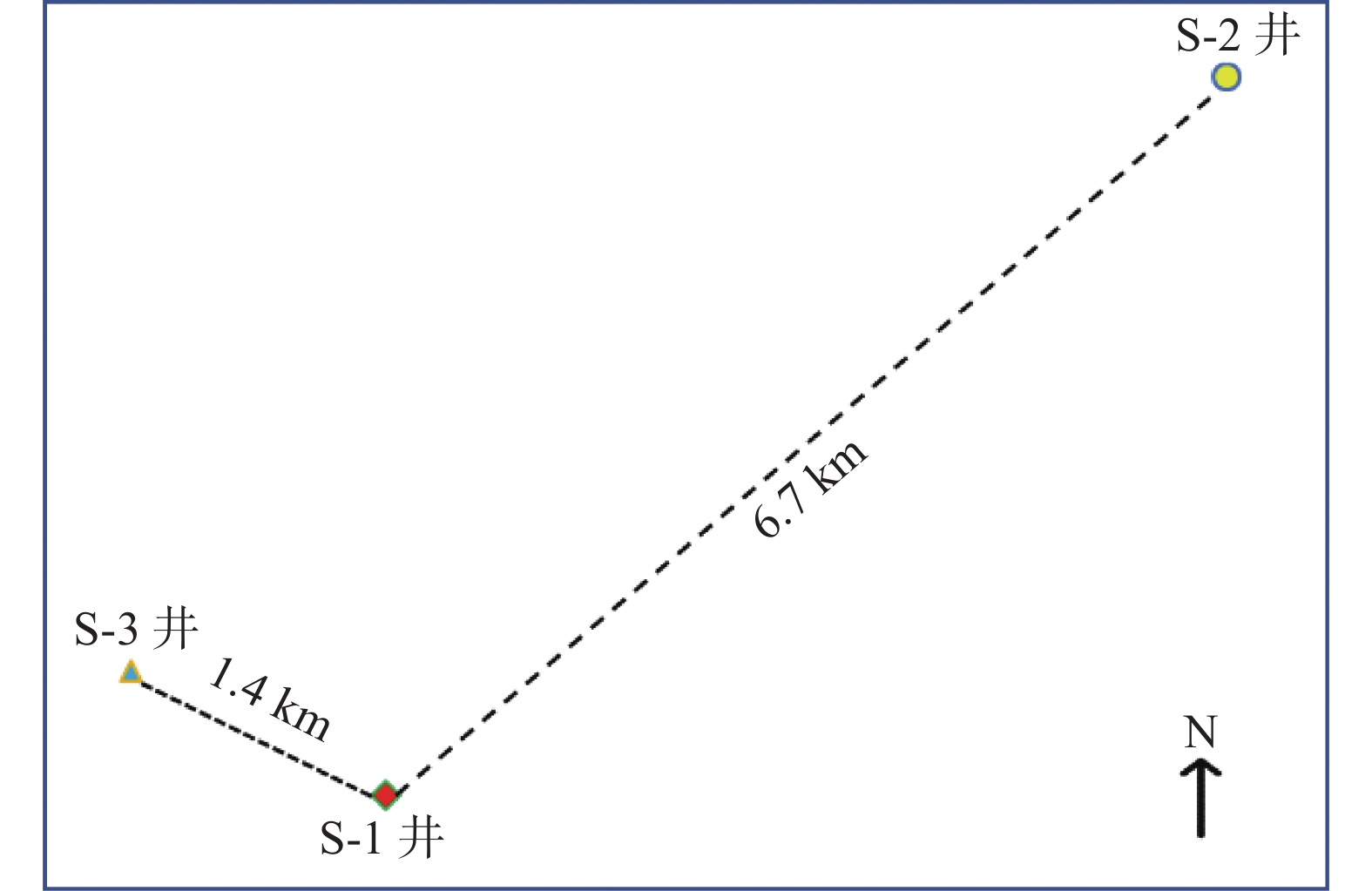
3口井均自上而下依次钻遇柳浪组、玉泉组、龙井组、花港组和平湖组,其中S-3井继续钻进至宝石组。3口井的主要目的层均位于平湖组中下段,且花港组(包括上段和下段)钻井复杂问题频发,所以本文的重点关注层位为花港组和平湖组。本文以S-1井作为训练井,S-1井的地层密度、孔隙压力和破裂压力剖面如图3所示,S-2井和S-3井作为目标预测井(即测试井)。地理位置上,S-2井西南距S-1井6.7 km,S-3井距离东南侧的S-1井1.4 km,3口井的井位分布图如图4所示。三口井共有的层位为花港组和平湖组,其中花港组岩性为浅灰色细砂岩、粉砂岩与绿灰色泥岩不等厚互层。平湖组岩性以灰色、深灰色泥岩、粉砂质泥岩为主,夹浅灰色粉砂岩、泥质粉砂岩等。本文作为训练井的S-1井各项数据经过严谨计算并进行了多次的现场验证比对,准确性很高,3口井的研究井段如表1所示。

|
| 图 3 S-1井输入层学习样本数据图 |
|
| 图 4 3口井井位分布图 |
| 井号 | 开始深 度/m |
结束深 度/m |
预处理后有效 数据量/行 |
| S-1 | 2112 | 4657 | 508 |
| S-2 | 2500 | 4770 | 449 |
| S-3 | 2888 | 4703 | 358 |
2.2 预测模型的建立
LightGBM破裂压力预测模型的建立流程如图5所示。首先确定模型的输入层变量,然后对学习样本数据进行预处理,数据的预处理对于模型的预测准确性具有很大影响。数据预处理操作主要包括异常值清理、缺失值补充和数据归一化等。本文以S-1井的井深、孔隙压力当量密度和地层密度作为输入层。计算孔隙压力和破裂压力时需要用到测井数据,而原始的测井数据往往首尾两端是明显错误的异常值,可直接删除,测井数据的内部也往往含有一些异常值,需要根据经验对异常值进行替换,一般替换成邻近数据的平均值。

|
| 图 5 LightGBM预测模型的建立流程图 |
预处理后便是划分数据集。本文将学习样本数据进行洗牌处理,将训练集与测试集按照7:3进行划分,并设置十折交叉验证集,可避免由于数据集划分不合理造成训练集过拟合问题。在建立模型的过程中,LightGBM算法相较于其他算法具有几个明显的特点,一是互斥特征捆绑(EFB),其优点在于保证预测准确性的基础上提升了模型的训练速度。二是直方图算法,能够显著提升模型的运算速度。三是按叶子生长,其他算法如XGBoost采用按层生长的增长策略,算法低效,而按叶子生长的一个显著优势在于,在分裂次数一致的情况下,该方法提高了预测精度,能有效减小误差。模型的基学习器采用GBDT(梯度提升决策树),其精度高且稳定。LightGBM是不断在当前基学习器的基础上去构建下一个基学习器,基学习器的数量对过拟合概率有很大影响,数量增加时会增强拟合能力,但同时也会增加过拟合的概率,本文设置为100个。合适的学习率能使目标函数在合适的时间内收敛到局部最小值,本文设置为0.1。模型的各项参数配置详见表2。
| 参数名 | 参数值 |
| 基学习器 | GBDT |
| 基学习器数量 | 100 |
| 学习率 | 0.1 |
| L1正则项 | 0 |
| L2正则项 | 1 |
| 样本征采样率 | 1 |
| 树特征采样率 | 1 |
| 节点分裂阈值 | 0 |
| 叶子节点样本的最小权重 | 0 |
| 树的最大深度 | 10 |
| 叶子节点最小样本数 | 10 |
表3展示了交叉验证集、训练集和测试集的预测评价指标,通过量化指标来衡量LightGBM模型的预测效果。其中,通过交叉验证集的评价指标可以不断调整超参数,以得到可靠稳定的模型。本文选取的模型评价指标共有5个,分别为均方误差(mean square error, MSE)、均方根误差(root mean square error, RMSE)、平均绝对误差(mean absolute error, MAE)、平均绝对百分比误差(mean absolute percentage error, MAPE)、决定系数(r²)。由表3可知,LightGBM预测模型在5项评价指标上均表现十分优越,三类数据集的MSE均仅为0.001,且训练集和交叉验证集的r²均大于0.9。
| 数据集 | MSE | RMSE | MAE/(g·cm−3) | MAPE/% | r² |
| 训练集 | 0.001 | 0.012 | 0.008 | 0.415 | 0.958 |
| 交叉验证集 | 0.001 | 0.025 | 0.017 | 0.788 | 0.925 |
| 测试集 | 0.001 | 0.032 | 0.019 | 1.029 | 0.732 |
训练集的r2较大说明模型的拟合效果较好,选择的输入层变量与输出层数据间相关性好。验证集是从训练集中分出来的数据,所以和训练集较为接近,这就导致训练的模型在验证集上表现得和训练集接近。但测试集使用的数据与训练集、验证集的不同,分布上有一定的偏差就导致在测试集上表现不如训练集和验证集。测试集的r2虽然较训练集的r2小0.2,但测试集的r2超过0.7。由此可见LightGBM模型的精度和稳定性均很好。
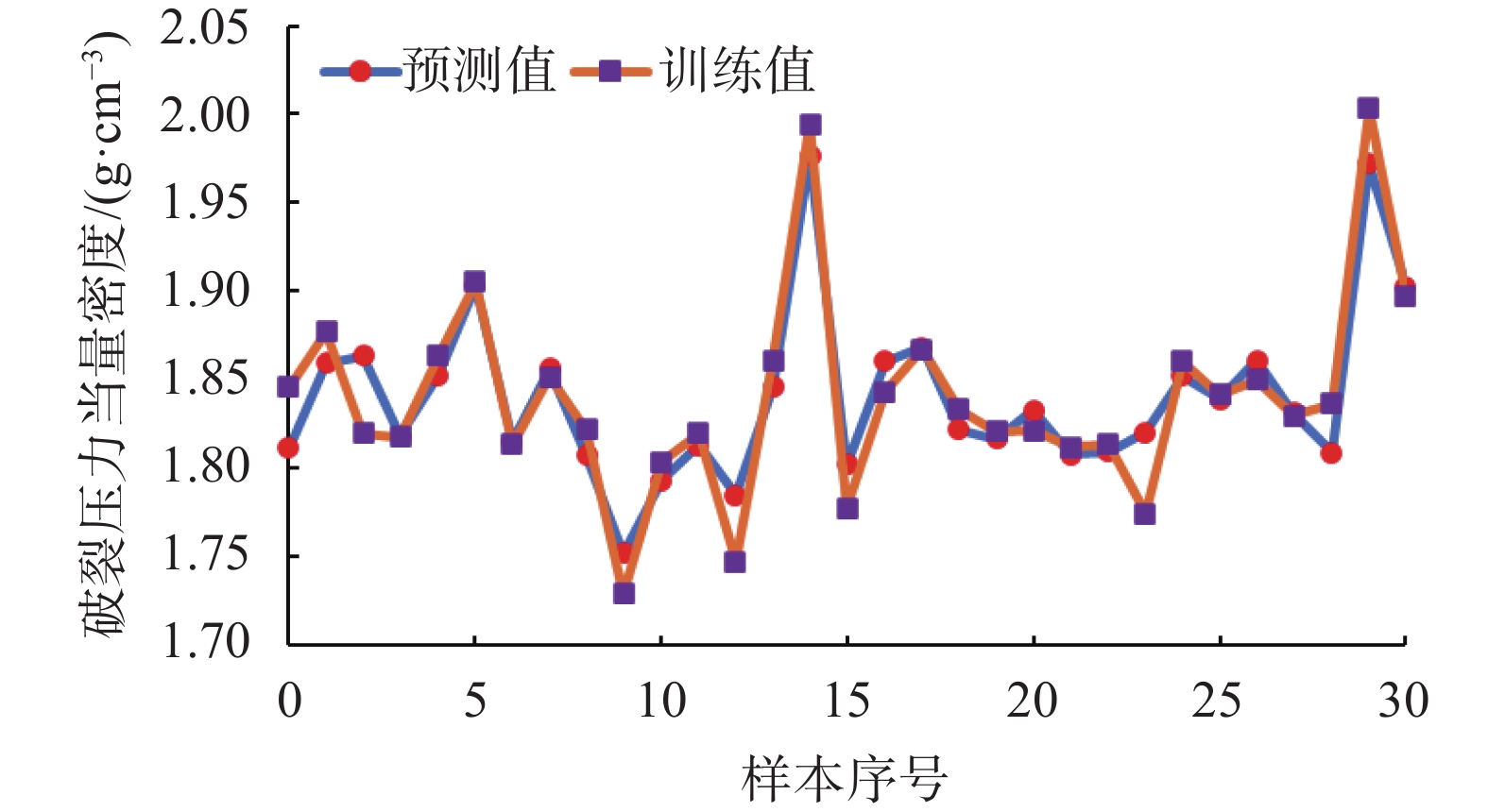
3 模型评价及参数敏感性分析 3.1 模型的预测结果分析通过对S-1井的部分破裂压力当量密度的预测值和训练值进行比对,可以发现训练值和预测值的趋势线基本吻合,LightGBM预测模型的建立符合实际情况,具体如图6所示。
|
| 图 6 S-1井部分训练数据预测值与训练值对比图 |
为了将LightGBM预测模型和传统破裂压力预测模型进行准确度比对,本文采用油田现场常用的声波测井资料法和LightGBM预测模型进行比对,以此来确定这两种模型的预测准确性。利用上文建立的LightGBM算法模型和声波测井资料法预测计算了S-1井的两口邻井S-2井和S-3井的破裂压力,将两种方法的计算结果分层位做出了压力纵剖图分别如图7和图8所示。通过图7和图8的比对可以发现,声波测井资料法所得到的预测破裂压力数据波动比LightGBM预测模型所得数据波动更加明显,而且在大多数层位,声波测井资料法所得数据要比LightGBM模型所得数据偏大。本文所重点关注的层位是复杂情况频发的花港组和主要目的层平湖组,在这两个层位上,声波测井资料法所得计算结果波动幅度和频率均很大,其预测结果明显存在不合理处,不适于安全钻井液密度窗口的设计。

|
| 图 7 S-2井分层位破裂压力预测剖面图 |

|
| 图 8 S-3井分层位破裂压力预测剖面图 |
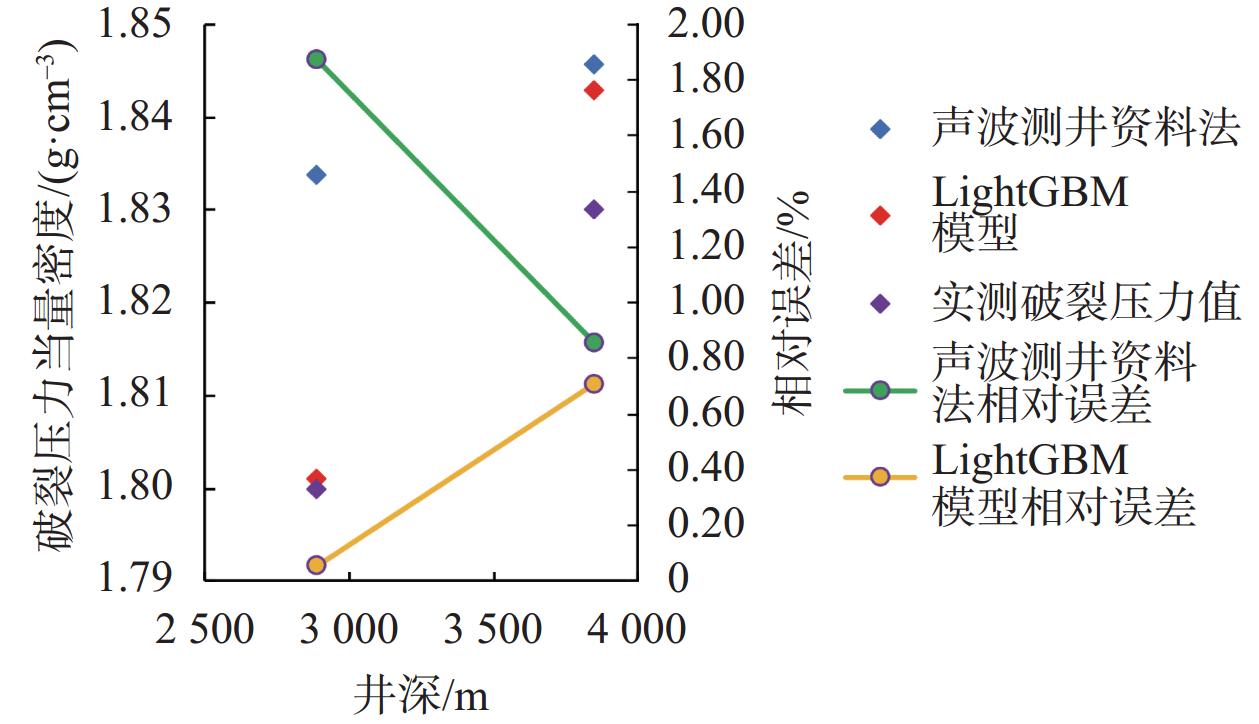
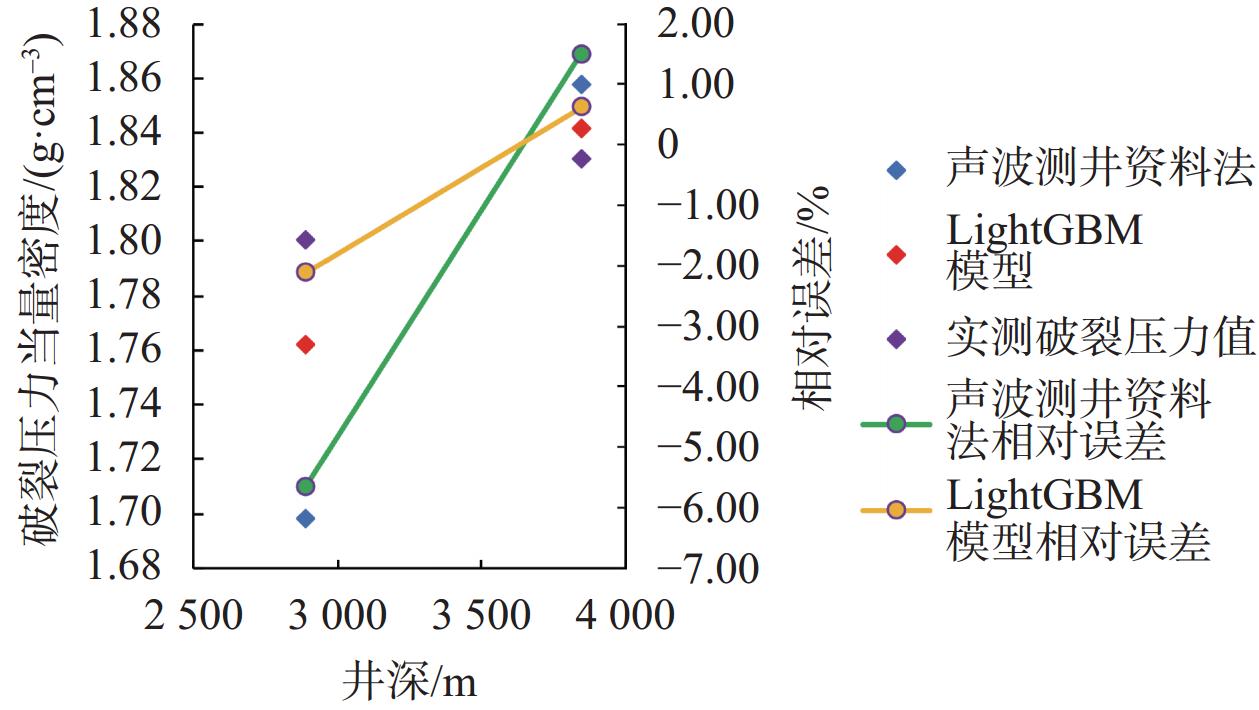
图9和图10分别展示了S-2井和S-3井的破裂压力实测值与上述两种方法的预测值的相对误差。对实测值进行误差分析可得,无论是S-2井还是S-3井,LightGBM算法模型的预测误差始终小于声波测井资料法。四个实测破裂压力点中,LightGBM模型的预测结果有3个点相对误差小于1%,1个点相对误差小于2%。LightGBM模型的预测值更接近真实值。
|
| 图 9 S-2井破裂压力预测误差图 |
|
| 图 10 S-3井破裂压力预测误差图 |
本文优选的输入层数据为井深、地层孔隙压力当量密度和地层密度,其中井深和地层密度通过测井资料获得,孔隙压力当量密度也是由测井资料计算得到,采用测井资料的显著优点在于每口井均具备测井资料并且其连续性好。在获得数据这一方面,本文采用的方法无需进行岩石力学实验,避免了一些井没有取岩心或岩心无法实验等弊端,从数据的获取方面具有普适性,具有显著的优势。
其次,本文利用S-1井训练好的模型预测了S-2井和S-3井。S-1井的地层层位自上而下依次为玉泉组、龙井组、花港组和平湖组,S-2井的层位依次为龙井组、花港组和平湖组,S-3井的层位依次为龙井组、花港组、平湖组和宝石组,3口井的地层层位并不完全相同。在三口井的直线距离并不很近并且地层层位不完全相同的情况下,利用LightGBM算法建立的模型其预测误差均不超过2%。对于其他区块而言,其地层层位与S区块不同,测井数据也有较大差异,但通过以上能够很好的说明LightGBM算法预测模型的普适性。
总的来看,传统破裂压力计算公式法中一些参数的选取受到人们主观经验因素的影响,这对预测精度的影响很大。而LightGBM模型的显著优势是在确保高精度的基础上,既减少了人为调参的经验不确定性,又大大节省了时间成本,明显优于传统的计算公式法。
3.2 模型参数敏感性分析为了量化分析输入层变量(即井深、孔隙压力当量密度和地层密度)对输出层变量(即破裂压力当量密度)的影响程度,以便后期进一步精准模型预测结果,本文采用灰色关联分析法对各参数间进行敏感性分析。选择S-1井预处理后的学习样本数据,将3种输入层变量作为特征序列,输出层变量作为母序列(对比序列),求解母序列(对比序列)和特征序列之间的灰色关联系数值,然后求解灰色关联度值并排序。本文分辨系数取0.5。
图11展示了输入层变量与输出层变量间的关联系数。关联系数反映了样本数据间的关联程度,系数越大,关联性越强。表4展示了输入层变量与输出层变量间的关联度大小及排序。关联度表示输入层各变量与输出层变量之间的相似关联程度,其是由关联系数进行计算平均值得出,关联度值介于0~1之间,该值越大表示变量间的相关性越强,关联度越高。由表4知,关联度最大的为地层密度,关联度最小的是井深,所以地层密度对于破裂压力的预测最为敏感,孔隙压力当量密度和井深次之,建议后续工作中在数据预处理等方面对地层密度重点关注,如地层密度缺失值的合理补充与矫正。

|
| 图 11 S-1井样本数据关联系数图 |
4 结束语
1)针对传统地层破裂压力预测方法中存在的适用条件单一、普适性不高、预测精度低等问题,本文提出了一种基于LightGBM机器学习算法的地层破裂压力预测新方法。LightGBM算法是一种高效梯度提升决策树算法,相较于传统的GBDT算法,其在不降低预测精度情况下,减少训练时间,降低了内存的占用。同时,LightGBM采用带深度限制的叶子生长策略,既能防止模型的过拟合,又能保证模型的高性能。
2)以S区块的3口直井为例验证了LightGBM模型的准确性并与传统的声波测井资料法进行比对分析。结果表明,声波测井资料法的破裂压力预测结果在绝大部分层位上都要较LightGBM模型的预测结果偏大,且声波测井资料法预测结果的波动性更加明显。经与实测破裂压力数据进行误差分析发现,LightGBM模型的预测相对误差均小于2%,其预测误差始终小于声波测井资料法。这表明,利用LightGBM回归算法建立破裂压力预测模型是可行的,其模型的预测准确性、稳定性和泛化性十分优越,远胜于传统的声波测井资料法。
3)为了进一步提高模型的预测效果,采用灰色关联分析法对模型的输入层变量,包括井深、孔隙压力当量密度和地层密度进行参数敏感性分析,结果表明地层密度与预测结果的关联度最大,孔隙压力当量密度和井深次之,建议对地层密度数据的准确性和全面性进行重点关注。
| [1] |
张东东, 刘文汇, 王晓锋, 等. 深层油气藏成因类型及其特征[J].
石油与天然气地质, 2021, 42(5): 1169-1180.
ZHANG D D, LIU W H, WANG X F, et al. Genetic types and characteristics of deep oil and gas plays[J].
Oil & Gas Geology, 2021, 42(5): 1169-1180.
DOI:10.11743/ogg20210514 |
| [2] |
HUBBERT M K, WILLIS D G. Mechaics of hydraulic fracturing[J].
Petroleum Transactions, 1957, 210: 153-168.
|
| [3] |
EATON B A. Fracture gradient prediction and its application in oilfield operations[J].
Journal of Petroleum Technology, 1969, 21(10): 1353-1360.
DOI:10.2118/2163-PA |
| [4] |
STEPHEN R D. Prediction of fracture pressures for wildcat wells[J].
Journal of Petroleum Technology, 1982, 34(4): 863-872.
DOI:10.2118/9254-PA |
| [5] |
黄荣樽. 地层破裂压力预测模式的探讨[J].
华东石油学院学报, 1984, 8(4): 335-347.
HUANG R Z. A model for predicting formationfracture pressure[J].
Journal of China University of Petroleum(Edition of Natural Science), 1984, 8(4): 335-347.
|
| [6] |
何伊丽, 贺华, 侯彬彬, 等. 延长气田地层破裂压力模型研究[J].
内蒙古石油化工, 2021, 47(8): 98-100.
HE Y L, HE H, HOU B B, et al. Study on the formation fracture pressure model in Yanchang gas field[J].
Inner Mongolia Petrochemical Industry, 2021, 47(8): 98-100.
DOI:10.3969/j.issn.1006-7981.2021.08.032 |
| [7] |
马先林, 周德胜, 蔡文斌, 等. 基于可解释机器学习的水平井产能预测方法[J].
西南石油大学学报(自然科学版), 2022, 44(4): 81-90.
MA X L, ZHOU D S, CAI W B, et al. An interpretable machine learning approach to prediction horizontal well productivity[J].
Journal of Southwest Petroleum University(Science & Technology Edition), 2022, 44(4): 81-90.
|
| [8] |
孙岿. 基于改进KNN算法的潜山复杂岩性测井识别方法[J].
特种油气藏, 2022, 29(3): 18-27.
SUN K. Logging identification method of complex lithology in buried hill based on the improved KNN algorithm[J].
Special Oil & Gas Reservoirs, 2022, 29(3): 18-27.
DOI:10.3969/j.issn.1006-6535.2022.03.003 |
| [9] |
宋先知, 姚学喆, 李根生, 等. 基于LSTM-BP神经网络的地层孔隙压力计算方法[J].
石油科学通报, 2022, 7(1): 12-23.
SONG X Z, YAO X Z, LI S G, et al. A novel method to calculate formation pressure based on the LSTM-BP neural network[J].
Petroleum Science Bulletin, 2022, 7(1): 12-23.
DOI:10.3969/j.issn.2096-1693.2022.01.002 |
| [10] |
李华洋, 吴惠梅, 南冲, 等. 南海深水L-1井区地层压力预测技术研究及应用[J].
石油地质与工程, 2020, 34(3): 113-117.
LI H Y, WU H M, NAN C, et al. Study and application of formation pressure prediction technology in deep water L-1 well area of south China sea[J].
Petroleum Geology and Engineering, 2020, 34(3): 113-117.
DOI:10.3969/j.issn.1673-8217.2020.03.024 |
| [11] |
林涛, 严寒, 赵丹阳. 基于IWOA-LightGBM的主轴轴承故障预警研究[J]. 中国测试, 2023, 49(5): 82-88.
LIN T, YAN H, ZHAO D Y. Research on fault early warning of spindle bearing based on IWOA-LightGBM[J]. China Measurement & Test, 2023, 49(5): 82-88.
|
| [12] |
张航, 史兆培, 束垠, 等. 基于OOB-BO-LightGBM的风电机组故障诊断方法[J/OL]. 中国测试: 1-7[2022-12-04]. http://kns.cnki.net/kcms/detail/51.1714.TB.20220623.1608.040.html.
ZHANG H, SHI Z P, SHU Y, et al. Fault diagnosis method of wind turbine based on OOB-BO-LightGBM[J/OL]. China Measurement & Test: 1-7[2022-12-04]. https://kns.cnki.net/kcms/detail/51.1714.TB.20220623.1608.040.html.
|
| [13] |
陈维刚, 张会林. 基于RF-LightGBM算法在风机叶片开裂故障预测中的应用[J].
电子测量技术, 2020, 43(1): 162-168.
CHEN W G, ZHANG H L. Application of RF-LightGBM algorithm in early warning of fan blade cracking[J].
Electronic Measurement Technology, 2020, 43(1): 162-168.
DOI:10.19651/j.cnki.emt.1903316 |
| [14] |
夏宏泉, 张元泽, 陈平, 等. 碳酸盐岩地层破裂压力的测井预测研究[J].
天然气工业, 2004(8): 32-35.
XIA H Q, ZHANG Y Z, CHEN P, et al. Log prediction of carbonate formation breakdown pressure[J].
Natural Gas Industry, 2004(8): 32-35.
DOI:10.3321/j.issn:1000-0976.2004.08.011 |
| [15] |
李昌盛, 宋海, 肖莉, 等. 基于遗传算法优化BP神经网络的地层破裂压力预测方法[J].
西安石油大学学报(自然科学版), 2015, 30(5): 75-79,10.
LI C S, SONG H, XIAO L, et al. Prediction method of formation fracture pressure based on BP neural network optimized by genetic algorithm( GA)[J].
Journal of Xi’an Shiyou University(Natural Science Edition), 2015, 30(5): 75-79,10.
|
 2024, Vol. 50
2024, Vol. 50


 ,
,