文章信息
- 郑传磊, 李淑翔, 孙呈凯, 金宝宏
- ZHENG Chuanlei, LI Shuxiang, SUN Chengkai, JIN Baohong
- 纤维再生粗骨料混凝土冻融损伤及寿命预测
- Freeze-thaw damage and life prediction of fiber recycled coarse aggregate concrete
- 中国测试, 2024, 50(3): 29-36
- CHINA MEASUREMENT & TEST, 2024, 50(3): 29-36
- http://dx.doi.org/10.11857/j.issn.1674-5124.2022040071
-
文章历史
- 收稿日期: 2022-04-12
- 收到修改稿日期: 2022-06-13
2. 中建八局第二建设有限公司,山东 济南 250014
2. The Second Construction Limited Company of China Construction Eighth Engineering Division, Jinan 250014, China
我国有53.5%的土地位于寒冷地带[1]。对于寒冷地带的混凝土建筑而言,季节温差大及昼夜温差大等因素对其造成的冻融损伤影响了建筑结构的长期安全使用及使用寿命。再生混凝土由于其内部再生骨料具有多孔隙多裂缝等缺陷,使其抗冻性能较差。因此,若想将再生混凝土以任何形式应用于工程建设中,对再生混凝土进行抗冻性能测试是非常必要的。研究表明,运用数学方法对混凝土的抗冻性能进行预测可显著节省试验时间和成本。
当前,众多学者基于数学方法建立宏观模型,如用残余抗压强度建立冻融损伤模型[2],但在实际工程中测试外界混凝土经冻融损伤后的残余抗压强度较为困难。也有学者从微观层面描述混凝土的冻融损伤模型。Jin等[3]基于分形维数建立混凝土冻融损伤模型,从微观层面通过孔径分布曲线及孔隙体积直方图定性分析混凝土内部的损伤形态及演化过程,但混凝土内部成分的离散性增加了取样难度,影响了模型精度,且测试成本较高。Wang等[4]通过应用疲劳损伤力学理论建立天然浮石混凝土的冻融损伤模型。结果表明:以相对动弹性模量作为物理损伤指标的冻融损伤模型可以有效为研究天然浮石混凝土的冻融损伤机理提供理论支持。相对动弹性模量作为一种易测且直观的试验参数,使用其建立混凝土的冻融损伤模型具有较好的实用性与经济性。相对动弹性模量数据具备信息不完全和贫信息的不确定性系统特征,具备典型的“灰色”特质。灰色系统理论作为一种相对成熟的控制理论,已在多个专业领域有相关应用研究[5]。以相对动弹性模量作为物理损伤指标运用灰色系统理论建立混凝土的冻融损伤模型可实现对“灰色”特质系统发展规律的定量预测。
在本项研究中,本文以再生粗骨料替代石子的替代率为变量,通过进行PVA纤维再生混凝土的抗冻性能试验,研究再生粗骨料替代率对混凝土抗冻性能的影响,同时建立冻融损伤模型,并以相对动弹性模量作为物理损伤指标基于GM(1,1)模型的原始差分(ODGM)、均值(EGM)、均值差分(EDGM)及离散(DGM) 4种形式对混凝土的抗冻性能进行灰色系统理论分析,为再生混凝土在寒冷地带的工程应用提供理论依据及技术支撑。
1 试验设计 1.1 试验原材料水泥:赛马牌42.5R普通硅酸盐水泥。粉煤灰:灵武市某发电厂生产的Ⅰ级灰。石子:银川市兰山砂石厂生产的碎石。再生粗骨料:宁夏大学校内废弃路面板混凝土经多道工序处理后得到的碎石。砂:银川市兰山砂石厂生产的水洗中砂。PVA纤维:可乐丽公司产品。减水剂:慕湖牌聚羧酸高效减水剂。水:银川市城市自来水。
1.2 混凝土配合比设计及试件制备表1为基准混凝土配合比。混凝土设计目标为C30强度泵送混凝土,试验时将通过调整减水剂的用量使混凝土的坍落度近似于180 mm。减水剂掺量为0.7%~1.2%。试验共设计9组混凝土,命名为R0、R30、R40、R50、R60、R70、R80、R90和R100,其中R代表再生混凝土,数字代表再生粗骨料替代率。为增强混凝土的性能,在混凝土中掺入0.10%体积分数的PVA纤维[6]。
在制作混凝土试件之前,先使用干净湿抹布擦拭搅拌机及坍落度桶内壁。擦拭完成后,向搅拌机内依次倒入砂、水泥、粉煤灰、石子、再生粗骨料及PVA纤维,干拌120 s;倒入减水剂和水的混合液,搅拌60 s。搅拌结束后,先测试混凝土的坍落度。若坍落度达到要求,再将混凝土倒入塑料模具,在振动台上振捣抹面。试件在室温下静置24 h后脱膜,再将试件移入标准养护室养护。
1.3 试验方法100 mm×100 mm×100 mm试件标养28 d后,用万能试验机测试抗压及劈拉强度。100 mm×100 mm×400 mm试件标养24 d后,将试件浸没于(20±2) ℃的水中浸泡4 d,使用混凝土快速冻融机对其进行冻融试验。冻融试验方法为快冻法。当冻融次数达到0、25、50、75、100及125次时,测试其质量及相对动弹性模量。当质量损失大于5%或相对动弹性模量小于60%时,判定混凝土失效[7]。
2 抗压及劈拉强度试验结果及分析从图1可以看出,混凝土的抗压及劈拉强度随再生粗骨料替代率的增加均呈现先减小后增加再减小的变化趋势,其大致在50%和70%替代率处出现两次拐点;拉压比大致呈现先减小后增加的变化趋势,其在80%替代率时为最小值。

|
| 图 1 再生粗骨料替代率对混凝土抗压、劈拉强度及拉压比的影响 |
再生粗骨料相较石子其强度较低,其表面及内部存在较多孔隙裂缝,这些孔隙裂缝在混凝土受外力破坏时快速扩展,使得掺再生粗骨料的混凝土强度较低[8]。再生混凝土内部存在石子-新砂浆、石子-旧砂浆及新砂浆-旧砂浆等粘结性较差的应力薄弱界面,当混凝土受到外力作用时,易在粘结薄弱处出现应力集中现象而损坏[9]。当再生粗骨料替代率从50%增至70%时,混凝土的抗压及劈拉强度出现了一段短暂的上升阶段,主要原因有:1)再生粗骨料大量吸水使得混凝土实际水胶比减小,强度增大[6];2)再生粗骨料在搅拌过程中吸收的部分水分会在试件养护的过程中逐渐释放出来,使得水化反应得以继续进行,从而促进强度的增长[10];3)较细的I级粉煤灰会对再生粗骨料的孔隙裂缝起到一定修补作用,继而增强再生混凝土的强度[11]。
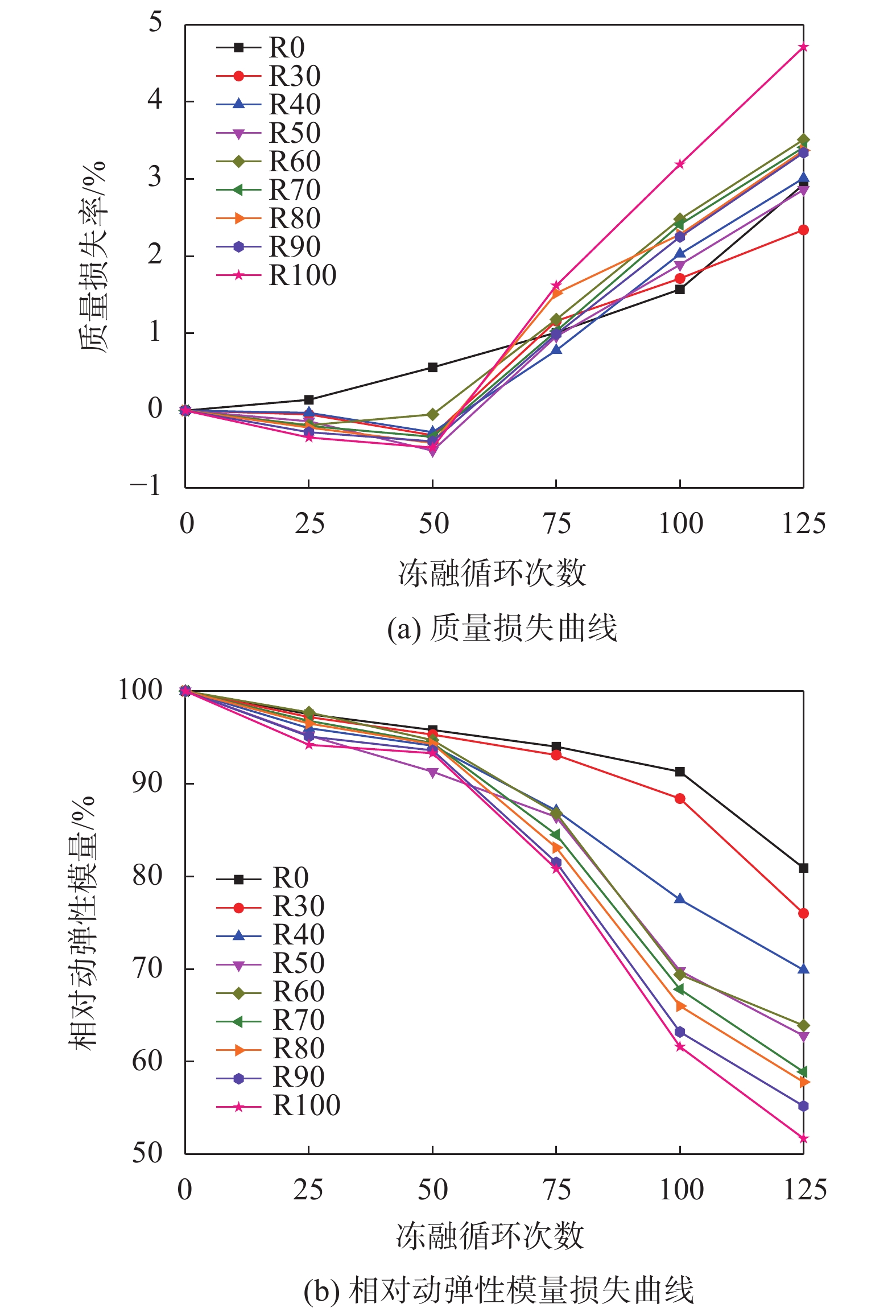
3 冻融试验结果及分析 3.1 结果分析图2(a)为质量损失率与冻融次数的关系曲线。从图2(a)可以看出,随着冻融循环次数的增加,除R0以外,其他混凝土在冻融循环初期都出现短暂负值,宏观上表现为质量的增加。分析原因为:再生粗骨料相较石子其吸水率较大,在冻融早期混凝土因冻融损伤而造成的砂浆及骨料剥蚀现象较为轻微,反而其内部孔隙裂缝中的自由水由于冷热循环产生的有害压力,造成混凝土在产生新的孔隙裂缝的同时扩大内部原有的孔隙裂缝,这些孔隙裂缝会逐渐从环境中吸收大量水分,吸水造成的试件增重大于骨料剥蚀的质量损失,使得试件增重。随着冻融次数的增加,混凝土的质量损失率呈现迅速增加,大致呈现出再生粗骨料替代率越大,质量损失率变化曲线斜率越大。再生粗骨料由于其品质劣势,使得再生粗骨料替代率越大时混凝土受到的损伤更为严重,宏观上表现为质量损失率的快速增加。
|
| 图 2 抗冻性能试验曲线 |
图2(b)为相对动弹性模量与冻融次数的关系曲线。从图2(b)可以看出,随着冻融循环次数的增加,各组混凝土的相对动弹性模量不断减小,在50~125次冻融循环次数时,各组混凝土曲线逐渐呈现“分层现象”。说明各组混凝土随着冻融次数的增加,相对动弹性模量衰变速率逐趋稳定。经历125次冻融次数后,各组混凝土的质量损失率皆小于5%,表明混凝土未破坏;而R70、R80、R90、R100的相对动弹性模量小于60%,表明混凝土已发生冻融破坏。说明使用相对动弹性模量来表述混凝土失效比质量损失更为敏感。
3.2 基于动弹性模量损伤的冻融损伤模型依据损伤力学理论[12],定义混凝土的冻融损伤变量为:
| $ {D_N} = 1 - \frac{{{E_N}}}{{{E_0}}} = {\rm ln}(a + bN) $ | (1) |
式中:
a和b——控制参数;
0及N——冻融次数。
使用式(1)对试验数据进行拟合,得到图3混凝土损伤值与冻融次数的拟合关系曲线及表2相对动弹性模量损伤模型拟合参数。在表2中,随着再生粗骨料替代率增大,拟合参数a逐渐减小,b逐渐增大。使用Design-Expert软件对a及b与再生粗骨料替代率之间的关系进行线性拟合,得到关系式公式(2)。在表2中,各组混凝土的相关性系数r2最低为0.7877,最高为0.9141,表明模型拟合精度较高,损伤值与冻融循环次数之间存在较好的相关性。在图3中,各组混凝土损伤值随着冻融循环次数的增加而增大;相同冻融次数时,损伤值随着再生粗骨料替代率的增大而增大。

|
| 图 3 混凝土损伤值与冻融次数的拟合关系曲线 |
| 分组 | R0 | R30 | R40 | R50 | R60 | R70 | R80 | R90 | R100 |
| a | 0.9844 | 0.977 | 0.9712 | 0.9633 | 0.9487 | 0.9447 | 0.9438 | 0.9451 | 0.9426 |
| b | 0.0014 | 0.0018 | 0.0027 | 0.0035 | 0.0035 | 0.0039 | 0.0041 | 0.0044 | 0.0047 |
| r2 | 0.7892 | 0.7877 | 0.9141 | 0.8872 | 0.8537 | 0.8587 | 0.8632 | 0.8652 | 0.8564 |
| $ \left\{ \begin{gathered} a = - 0.048\,9n + 0.986\,1,\;{r^2} = 0.880\,3 \\ b = 0.003\,5n + 0.001\,3,\;{r^2} = 0.939 \\ \end{gathered} \right. $ | (2) |
式中:
使用响应曲面多项式回归分析方法可以构建不同响应与应变量的关系[13]。根据图2混凝土冻融试验结果,使用Design-Expert软件中的Response Surface-Optimal模块构建二次模型进行拟合分析,得到质量损失率和相对动弹性模量与冻融次数及再生粗骨料替代率的响应曲面如图4、5所示,响应面回归方程如式(3)所示。从图4(a)、图5(a)及式(3)可以看出,试验所得试验值与预测值较为契合。图4(b)中响应曲面坡度较小,图5(b)中响应曲面坡度较大,说明冻融次数和再生粗骨料替代率对质量损失率影响不显著,对相对动弹性模量影响显著。

|
| 图 4 质量损失率响应曲面分析 |

|
| 图 5 相对动弹性模量响应曲面分析 |
| $ \left\{ \begin{gathered} \Delta W(N,n) = (3.076\,5E - 4){N^2} + (1.007E - 4){n^2} + \\ (1.614\,7E - 4) N \times n - 0.019\,4N - 0.017n + 0.464\,5, \\{r^2} = 0.928\,2 \\ \Delta E(N,n) = - 0.002{N^2} + (2.400\,6E - 4){n^2} - 0.002\,9N \times n + \\ 0.123\,6N + 0.021n + 97.588,{r^2} = 0.961 \\ \end{gathered} \right. $ | (3) |
式中:
依据邓聚龙教授[5]创立的灰色系统理论,基于GM(1,1)模型的ODGM、EGM、EDGM及DGM这4种形式对混凝土的相对动弹性模量进行灰色系统理论分析,并将模型试验值和预测值列于表3。
| % | ||||||||||||||||
| 冻融次数 | 0 | 25 | 50 | 75 | 100 | 125 | 冻融次数 | 0 | 25 | 50 | 75 | 100 | 125 | |||
| R0 | 试验值 | 100 | 97.5 | 95.8 | 94 | 91.3 | 80.9 | R70 | 试验值 | 100 | 96.8 | 94.4 | 84.5 | 67.8 | 58.9 | |
| ODGM | 100 | 99.4 | 95.51 | 91.76 | 88.16 | 84.7 | ODGM | 100 | 101.45 | 89.725 | 79.355 | 70.184 | 62.072 | |||
| EGM | 100 | 99.43 | 95.51 | 91.75 | 88.13 | 84.66 | EGM | 100 | 101.439 | 89.668 | 79.262 | 70.064 | 61.934 | |||
| EDGM | 100 | 99.44 | 95.521 | 91.757 | 88.141 | 84.668 | EDGM | 100 | 101.56 | 89.761 | 79.332 | 70.115 | 61.969 | |||
| DGM | 100 | 99.475 | 95.537 | 91.755 | 88.122 | 84.634 | DGM | 100 | 101.658 | 89.792 | 79.312 | 70.054 | 61.877 | |||
| R30 | 试验值 | 100 | 97.2 | 95.3 | 93.1 | 88.4 | 76 | R80 | 试验值 | 100 | 96.5 | 94.3 | 83.1 | 66 | 57.8 | |
| ODGM | 100 | 99.804 | 94.65 | 89.763 | 85.127 | 80.731 | ODGM | 100 | 101.263 | 89.057 | 78.323 | 68.882 | 60.579 | |||
| EGM | 100 | 99.839 | 94.654 | 89.739 | 85.079 | 80.66 | EGM | 100 | 101.248 | 88.994 | 78.224 | 68.756 | 60.435 | |||
| EDGM | 100 | 99.862 | 94.675 | 89.757 | 85.095 | 80.675 | EDGM | 100 | 101.38 | 89.094 | 78.297 | 68.809 | 60.47 | |||
| DGM | 100 | 99.916 | 94.698 | 89.752 | 85.064 | 80.622 | DGM | 100 | 101.483 | 89.127 | 78.275 | 68.745 | 60.375 | |||
| R40 | 试验值 | 100 | 96 | 94.1 | 87.1 | 77.5 | 69.9 | R90 | 试验值 | 100 | 95.1 | 93.6 | 81.5 | 63.2 | 55.2 | |
| ODGM | 100 | 98.924 | 91.378 | 84.409 | 77.971 | 72.024 | ODGM | 100 | 100.355 | 87.556 | 76.39 | 66.647 | 58.147 | |||
| EGM | 100 | 98.907 | 91.349 | 84.368 | 77.921 | 71.967 | EGM | 100 | 100.357 | 87.492 | 76.277 | 66.499 | 57.975 | |||
| EDGM | 100 | 98.957 | 91.391 | 84.404 | 77.951 | 71.991 | EDGM | 100 | 100.504 | 87.602 | 76.356 | 66.553 | 58.01 | |||
| DGM | 100 | 98.988 | 91.403 | 84.4 | 77.932 | 71.961 | DGM | 100 | 100.634 | 87.641 | 76.326 | 66.472 | 57.89 | |||
| R50 | 试验值 | 100 | 95.2 | 91.3 | 86.4 | 69.8 | 62.8 | R100 | 试验值 | 100 | 94.2 | 93.3 | 80.8 | 61.6 | 51.7 | |
| ODGM | 100 | 98.695 | 89.019 | 80.291 | 72.419 | 65.318 | ODGM | 100 | 100.167 | 86.593 | 74.859 | 64.715 | 55.945 | |||
| EGM | 100 | 98.698 | 88.982 | 80.222 | 72.325 | 65.205 | EGM | 100 | 100.197 | 86.53 | 74.727 | 64.534 | 55.732 | |||
| EDGM | 100 | 98.782 | 89.049 | 80.275 | 72.366 | 65.236 | EDGM | 100 | 100.364 | 86.651 | 74.812 | 64.591 | 55.766 | |||
| DGM | 100 | 98.86 | 89.076 | 80.261 | 72.319 | 65.162 | DGM | 100 | 100.533 | 86.701 | 74.771 | 64.484 | 55.611 | |||
| R60 | 试验值 | 100 | 97.7 | 94.7 | 86.8 | 69.4 | 63.9 | |||||||||
| ODGM | 100 | 101.56 | 91.016 | 81.566 | 73.097 | 65.508 | ||||||||||
| EGM | 100 | 101.554 | 90.97 | 81.489 | 72.996 | 65.388 | ||||||||||
| EDGM | 100 | 101.651 | 91.047 | 81.549 | 73.042 | 65.422 | ||||||||||
| DGM | 100 | 101.732 | 91.075 | 81.533 | 72.992 | 65.345 | ||||||||||
3.4.1 GM(1,1)模型精度检验
将试验值记为原始序列,记为
| $ {X^{(0)}} = ({x}^{(0)}(1),{x}^{(0)}(2), \cdot \cdot \cdot ,{x}^{(0)}(s)) $ | (4) |
| $ {X^{(1)}} = ({x}^{(1)}(1),{x}^{(1)}(2), \cdot \cdot \cdot ,{x}^{(1)}(s)) $ | (5) |
计算GM(1,1)模型4种形式的模型精度,并参照表4精度评定参照表评定模型精度预测等级,将结果列于表5。从表5可以看出,除R0和R30的C值大于0.35,其他组均小于0.35;P值所有组均大于0.95。故R0和R30模型精度评为Ⅱ级,R40、R50、R60、R70、R80、R90及R100模型精度评为Ⅰ级。
| 分组 | 预测模型 | C | P | 预测等级 | 分组 | 预测模型 | C | P | 预测等级 | |
| R0 | ODGM | 0.3813318 | 1 | Ⅱ | R70 | ODGM | 0.2455991 | 1 | Ⅰ | |
| EGM | 0.3816019 | 1 | Ⅱ | EGM | 0.2456136 | 1 | Ⅰ | |||
| EDGM | 0.3815531 | 1 | Ⅱ | EDGM | 0.2455645 | 1 | Ⅰ | |||
| DGM | 0.3815687 | 1 | Ⅱ | DGM | 0.2456114 | 1 | Ⅰ | |||
| R30 | ODGM | 0.3721173 | 1 | Ⅱ | R80 | ODGM | 0.2417353 | 1 | Ⅰ | |
| EGM | 0.3720797 | 1 | Ⅱ | EGM | 0.241755 | 1 | Ⅰ | |||
| EDGM | 0.3721087 | 1 | Ⅱ | EDGM | 0.2417192 | 1 | Ⅰ | |||
| DGM | 0.3721413 | 1 | Ⅱ | DGM | 0.2417686 | 1 | Ⅰ | |||
| R40 | ODGM | 0.2023824 | 1 | Ⅰ | R90 | ODGM | 0.255264 | 1 | Ⅰ | |
| EGM | 0.2023789 | 1 | Ⅰ | EGM | 0.2552924 | 1 | Ⅰ | |||
| EDGM | 0.202358 | 1 | Ⅰ | EDGM | 0.2552245 | 1 | Ⅰ | |||
| DGM | 0.2023579 | 1 | Ⅰ | DGM | 0.2553129 | 1 | Ⅰ | |||
| R50 | ODGM | 0.2495008 | 1 | Ⅰ | R100 | ODGM | 0.2735435 | 1 | Ⅰ | |
| EGM | 0.2495157 | 1 | Ⅰ | EGM | 0.2735534 | 1 | Ⅰ | |||
| EDGM | 0.2494953 | 1 | Ⅰ | EDGM | 0.2734968 | 1 | Ⅰ | |||
| DGM | 0.2495387 | 1 | Ⅰ | DGM | 0.2735849 | 1 | Ⅰ | |||
| R60 | ODGM | 0.2481363 | 1 | Ⅰ | ||||||
| EGM | 0.2481484 | 1 | Ⅰ | |||||||
| EDGM | 0.2481217 | 1 | Ⅰ | |||||||
| DGM | 0.2481616 | 1 | Ⅰ | |||||||
为进一步比较GM(1,1)模型4种形式的预测精度,引入精度系数S2。将表3数据代入公式(6),计算结果列于表6。从表6可以看出,无论再生粗骨料替代率如何,DGM的精度最大,ODGM的精度最小。
| 预测模型 | R0 | R30 | R40 | R50 | R60 | R70 | R80 | R90 | R100 |
| ODGM | 0.8357 | 0.8361 | 0.9409 | 0.9105 | 0.9116 | 0.9057 | 0.9082 | 0.8979 | 0.88 |
| EGM | 0.8419 | 0.8438 | 0.9443 | 0.9167 | 0.9177 | 0.9121 | 0.9145 | 0.9055 | 0.8894 |
| EDGM | 0.8414 | 0.8435 | 0.9442 | 0.9172 | 0.9186 | 0.9134 | 0.916 | 0.9072 | 0.8914 |
| DGM | 0.8471 | 0.8506 | 0.9474 | 0.9232 | 0.9249 | 0.9202 | 0.9229 | 0.9153 | 0.9012 |
| $ {S^2} = \frac{{\rm SSR}}{{\rm SST}} = \frac{{\displaystyle \sum\limits_{i = 1}^s {(x_i^{(1)} - \bar x )} }}{{\displaystyle \sum\limits_{i = 1}^s {(x_i^{(0)} - \bar x )} }} = 1 - \frac{{\displaystyle \sum\limits_{i = 1}^s {(x_i^{(0)} - \bar x )} }}{{\displaystyle \sum\limits_{i = 1}^s {(x_i^{(1)} - \bar x )} }} $ | (6) |
其中,
内蒙古地区地域辽阔,纬度高,经度跨越大,冬季结冰时间长,以内蒙古地区为例对再生混凝土进行抗冻耐久性服役寿命预测对推广再生混凝土在生产实践中的使用具有一定现实意义。
根据武海荣等[14]的研究表明,内蒙古地区室外环境年平均冻融循环次数为120次,室内冻融1次约为室外冻融12次。按照式(7)[14]计算混凝土抗冻耐久性寿命,将结果列于表7。
| 年 | |||||||||
| 预测模型 | R0 | R30 | R40 | R50 | R60 | R70 | R80 | R90 | R100 |
| ODGM | 34 | 29 | 20 | 15 | 14 | 13 | 13 | 12 | 12 |
| EGM | 34 | 29 | 20 | 15 | 14 | 13 | 13 | 12 | 12 |
| EDGM | 34 | 29 | 20 | 15 | 14 | 13 | 13 | 12 | 12 |
| DGM | 34 | 29 | 20 | 15 | 14 | 13 | 13 | 12 | 12 |
| $ t = \frac{{k{N_{\max }}}}{M} $ | (7) |
式中:
从表7可以看出,4种形式计算的混凝土抗冻耐久性寿命相同;随着再生粗骨料替代率的增加,混凝土抗冻耐久性寿命逐渐减小;相比未掺再生粗骨料,再生粗骨料替代率以10%的增量从30%增至100%时,混凝土抗冻耐久性寿命分别减少14.71%、41.18%、55.88%、58.82%、61.76%、61.76%、64.71%及64.71%;再生粗骨料从0%增至50%时混凝土抗冻耐久性寿命减少较多,从50%增至100%时抗冻耐久性寿命减速放缓。
4 结束语1)随着再生粗骨料替代率的增加,混凝土的抗压及劈拉强度呈现先减小后增加再减小的变化趋势,其在50%和70%替代率处出现两次拐点;拉压比大致呈现先减小后增加的变化趋势,其在80%替代率时为最小值。
2)随着冻融循环次数的增加,混凝土的质量损失率不断增大,相对动弹性模量不断减小;125次冻融次数后,各组混凝土的质量损失率皆小于5%,部分混凝土组的相对动弹性模量小于60%,说明使用相对动弹性模量来表述混凝土失效比质量损失更为敏感。
3)随着再生粗骨料替代率的增大,混凝土损伤值与冻融次数的拟合关系曲线的拟合参数a逐渐减小,b逐渐增大;使用Design-Expert软件对拟合参数a及b与再生粗骨料替代率之间的关系进行线性拟合,结果表明两者之间存在较好的相关性。
4)使用Design-Expert软件构建质量损失率和相对动弹性模量与冻融次数及再生粗骨料替代率的响应曲面及回归方程,结果表明冻融次数和再生粗骨料替代率对质量损失率影响不显著,对相对动弹性模量影响显著。
5)基于灰色系统理论GM(1,1)模型的4种形式对混凝土的相对动弹性模量进行灰色系统理论分析。结果表明:R0和R30模型精度评为Ⅱ级,其他组评为Ⅰ级;无论再生粗骨料替代率如何,DGM的精度最大,ODGM的精度最小;以内蒙古地区为例计算混凝土抗冻耐久性寿命,发现4种形式计算的寿命相同,当再生粗骨料替代率大于50%后,再生粗骨料替代率对混凝土抗冻耐久性寿命影响较小。
| [1] |
谭忆秋, 徐慧宁, 周纯秀, 等. 季节性冰冻地区路基温度场分布规律[J].
哈尔滨工业大学学报, 2011, 43(8): 98-102.
TAN Y Q, XU H N, ZHOU C X, et al. Temperature distribution characteristic of subgrade in seasonally frozen regions[J].
Journal of Harbin Institute of Technology, 2011, 43(8): 98-102.
|
| [2] |
曹鑫铖, 金宝宏, 侯玉飞. 包浆再生粗骨料对自密实混凝土力学性能及抗冻性的影响[J].
土木与环境工程学报(中英文), 2022, 44(1): 149-159.
CAO X C, JIN B H, HOU Y F. Experimental study on the effect of the wrapped slurry recycled coarse aggregate on the mechanical properties and frost resistance of self-compacting concrete[J].
Journal of Civil and Environmental Engineering, 2022, 44(1): 149-159.
|
| [3] |
JIN S, ZHENG G, YU J. A micro freeze-thaw damage model of concrete with fractal dimension[J].
Construction and Building Materials, 2020, 257: 1-8.
|
| [4] |
WANG X, WU Y, SHEN X, et al. An experimental study of a freeze-thaw damage model of natural pumice concrete[J].
Powder Technology, 2018, 339: 651-658.
DOI:10.1016/j.powtec.2018.07.096 |
| [5] |
邓聚龙. 灰色系统理论教程[M]. 武汉: 华中理工大学出版社, 1990.
|
| [6] |
马楠, 王琳, 李迎乐. 干湿交替机制下PVA纤维增强混凝土抗硫酸盐侵蚀性能试验研究[J].
中国测试, 2021, 47(7): 142-147.
MA N, WANG L, LI Y L. Experimental study on sulfate corrosion resistance of PVA fiber reinforced concrete under alternate wetting and drying mechanism[J].
China Measurement & Test, 2021, 47(7): 142-147.
|
| [7] |
普通混凝土长期性能和耐久性能试验方法标准: GB/T 50082—2009[S]. 北京: 中国建筑工业出版社, 2009.
Standard for test methods of long-term performance and durability of ordinary concrete: GB/T 50082—2009[S]. Beijing: China Architecture & Building Press, 2009.
|
| [8] |
郑传磊, 王晋浩, 金宝宏, 等. 多因素对自密实混凝土力学性能发展趋势的影响[J].
功能材料, 2021, 52(12): 12022-12029,12035.
ZHENG C L, WANG J H, JIN B H, et al. The influence of many factors on the development trend of the mechanical properties of self-compacting concrete[J].
Journal of Functional Materials, 2021, 52(12): 12022-12029,12035.
|
| [9] |
商效瑀, 杨经纬, 李江山. 基于CT图像的再生混凝土细观破坏裂纹分形特征[J].
复合材料学报, 2020, 37(7): 1774-1784.
SHANG X Y, YANG J W, LI J S. Fractal characteristics of meso-failure crack in recycled coarse aggregate concrete based on CT image[J].
Acta Materiae Compositae Sinica, 2020, 37(7): 1774-1784.
|
| [10] |
肖建庄, 李佳彬, 孙振平, 等. 再生混凝土的抗压强度研究[J].
同济大学学报(自然科学版), 2004, 32(12): 1558-1561.
XIAO J Z, LI J B, SUN Z P, et al. Study on compressive strength of recycled aggregate concrete[J].
Journal of Tongji University(Natural Science), 2004, 32(12): 1558-1561.
|
| [11] |
李俊, 尹健, 周士琼, 等. 粉煤灰与矿渣对再生骨料混凝土力学性能影响的研究[J].
混凝土, 2005(6): 80-83,86.
LI J, YIN J, ZHOU S Q, et al. Mechanical properties of recycled aggregate concrete with fly ash and slag[J].
Concrete, 2005(6): 80-83,86.
|
| [12] |
余天庆, 钱济成. 损伤理论及其应用[M]. 北京: 国防工业出版社, 1998.
|
| [13] |
宋晶颖, 许玲玲, 买哲. 冻融循环与硫酸盐侵蚀耦合作用下纳米SiO2对混凝土性能影响研究[J]. 中国测试, 2022, 48(11): 174-179.
SONG J Y, XU L L, MAI Z. Study on the effect of nano-SiO2 on concrete performance under the combined action of freeze-thaw cycle and sulfate erosion[J]. China Measurement & Test, 2022, 48(11): 174-179.
|
| [14] |
武海荣, 金伟良, 延永东, 等. 混凝土冻融环境区划与抗冻性寿命预测[J].
浙江大学学报(工学版), 2012, 46(4): 650-657.
WU H R, JIN W L, YAN Y D, et al. Environmental zonation and life prediction of concrete in frost environments[J].
Journal of Zhejiang University(Engineering Science), 2012, 46(4): 650-657.
|
 2024, Vol. 50
2024, Vol. 50