文章信息
- 蔡晨宁, 严刚, 陈少林, 刘丽娜
- CAI Chenning, YAN Gang, CHEN Shaolin, LIU Li'na
- 基于电阻抗成像的智能混凝土结构损伤识别
- Damage detection for smart concrete structure by using electrical impedance tomography
- 中国测试, 2022, 48(11): 8-14
- CHINA MEASUREMENT & TEST, 2022, 48(11): 8-14
- http://dx.doi.org/10.11857/j.issn.1674-5124.2021080076
-
文章历史
- 收稿日期: 2021-08-11
- 收到修改稿日期: 2021-09-07
2. 南京航空航天大学航空学院,江苏 南京 210016;
3. 南京航空航天大学金城学院,江苏 南京 211156
2. College of Aerospace Engineering, Nanjing University of Aeronautics and Astronautics, Nanjing 210016, China;
3. Jincheng College, Nanjing University of Aeronautics and Astronautics, Nanjing 211156, China
混凝土是世界上第二大使用的资源,大多数基础设施都是采用混凝土建造。由于外部复杂使用环境的影响,混凝土材料不可避免会发生性能退化,造成混凝土结构损伤的产生及延展,严重危害结构的安全性和耐久性[1]。因此,如何能够快速有效地识别出损伤,是保证混凝土结构使用寿命的重要措施。近年来在结构健康监测技术领域已经发展了很多损伤识别方法[1-2],可以及时获取损伤信息并进行精准有效的监测预警,避免大型事故发生、保障混凝土结构的正常工作。
与传统结构损伤识别方法相比,在医学领域发展起来的电阻抗成像技术因成本低、对结构不造成损伤及信息可视化等优点而被引入了工程检测领域[3-5]。如Karhunen等人为一混凝土块设计电极阵列装置,通过电阻抗成像技术实现了损伤的三维可视化,表明电阻抗成像技术用于混凝土损伤监测是完全可行的[3];Ren等人进一步对多种电极装置情况下混凝土损伤电阻抗成像技术进行了研究,并考虑了水化反应对损伤识别的影响[4];余佳干等人发展了一种基于约束反问题优化的电阻抗成像算法,可以有效降低伪影,提高混凝土中损伤的定位精度[5]。但总体来说,混凝土材料本身导电性能不均匀、导电率非常低,对其直接应用电阻抗成像技术,影响损伤成像识别的效果。
为了解决这个问题,研究者提出通过加入功能材料和器件,使得混凝土具有自感知特性,并结合电阻抗成像技术实现结构自我监控或自我诊断[6-7]。如Hallaji等人将银浆涂覆在混凝土表面制备了感应层,能够感知裂纹和孔洞等损伤[8];Seppanen等人采用银浆和铜浆制备了两个感应层埋置在混凝土里,分别用于监测损伤和渗水[9];Downey等人在水泥中掺入总质量1%的多壁碳纳米管,提高混凝土的导电性能,通过其电阻变化感应损伤的存在[10]。但这些提供感应功能的材料成本较高,不适合在混凝土这类大体量结构推广应用。碳油墨因其具有成本低廉、导电性能良好、易于制备等特性,近来受到柔性传感领域的广泛关注,被应用到结构健康监测。如Zymelka等人通过丝网印刷技术将碳油墨印制在柔性基底上,制备成柔性应变传感器,并将其粘贴在结构试验件监测拉伸和疲劳试验下的应变响应,结果表明其具有较高灵敏度、准确性和可靠性[11]。Yan等人将碳油墨直接印刷在复合材料层板结构表面,通过对其电导率变化进行重建实现对损伤的监测和识别,结果表明印刷传感层对损伤具有很好的感知能力,可以准确反映损伤的信息[12]。但现有碳油墨印刷传感器大多应用于金属和复合材料结构,在混凝土材料和结构的应用鲜有报道;传感器大多为单次使用,在感应层受损后,未能对受损的传感区域进行修复,实现长期重复使用的目标。
本文提出将低成本的石墨烯导电碳油墨作为功能材料集成在混凝土表面作为传感层,形成具有自感知能力的智能混凝土,通过电阻抗成像技术实现多个损伤的监测识别,确定损伤的基本信息;在此基础上,对已受损的传感层进行人工修复,并通过实验考核智能传感层再利用的功能特性,验证了本文所提出技术和方法的有效性。
1 电阻抗成像原理电阻抗成像是一种低成本、操作简单的无损成像技术。其主要过程包括:1)将电极阵列布置在待测场域边界;2)激励微小的电流来分别获得损伤前后的边界电压信号;3)对电压信号进行处理,结合电学成像算法重建目标场域电导率变化分布图像,从而反映损伤的位置及形状尺寸等信息。
采用电阻抗成像识别损伤属于典型的反问题,在此之前需先求解正问题,即在已知电导率分布的条件下,求解场域内部及边界电势分布。当注入的电流为直流时,场域内电压-电流关系可采用拉普拉斯方程以及相应的边界条件来描述,即:
| $ {\varOmega }: {{\nabla}} \cdot{ (\sigma \nabla \varphi )}=0 $ | (1) |
| $ {\varGamma }_{1} : \varphi ={\varphi }_{0} $ | (2) |
| $ {\varGamma }_{2} : \sigma \frac{\delta \varphi }{\delta n}=-{J}_{n} $ | (3) |
式中:Ω——场域;
n——边界法线方向。
求解正问题的主要目的是获得边界电压值变化和电导率变化之间的关系,即灵敏度矩阵
| $ {A}_{ij}={\int }_{\varOmega }\nabla {u}_{i}\cdot \nabla {u}_{j}{\rm d}\varOmega $ | (4) |
式中:
Aij——对应的灵敏度矩阵元素。
电阻抗成像的反问题是由边界测量电压信号值通过重建计算,获得场域内的电导率分布,一般采用灵敏度矩阵来求解场域内电导率的变化量,即:
| $ \Delta V=A\Delta \sigma $ | (5) |
其中
由于灵敏度矩阵是病态的,式(5)不能直接取逆求解场域内电导率的变化量,需采用最小二乘法,即:
| $ \Delta {\sigma }^{*}=\mathit{\rm arg}\underset{\Delta \sigma }{\rm min}\left({\left\|{\boldsymbol A}\Delta \sigma -\Delta V\right\|}^{2}\right) $ | (6) |
其中
但式(6)仍可能具有不适定性,需使用正则化方法获得稳定解,Tikhonov正则化是一种常用的正则化方法,通过引入正则化项
| $ \Delta {\sigma }^{*}\text{={\rm arg}}\underset{\Delta \sigma }{\rm min}({\left\|{\boldsymbol{A}}\Delta \sigma -\Delta V\right\|}^{2}+{\left\|{\boldsymbol{L}}\Delta \sigma \right\|}^{2}) $ | (7) |
式中:
令式(7)右端泛函的导数为零,对应的
| $ \Delta {\sigma }^{*}=({{\boldsymbol{A}}}^{{\rm{T}}}{\boldsymbol{A}}+{\lambda }^{2}{\boldsymbol{I}}{)}^{-1}{{\boldsymbol{A}}}^{{\rm{T}}}\Delta V $ | (8) |
在Tikhonov正则化中,一个关键的因素是如何选择正则化参数。如参数值过小,残差项占主导,计算结果接近原问题解,解可能不稳定;如参数值过大,则罚函数项占主导,计算结果会偏离原问题解,影响解的准确性。本文采用L曲线法来确定合理的正则化参数[15],将式(7)中的残差项和正则化项进行对比,使得残差项和正则化项达到一种平衡关系。通常来说,对数坐标尺度下,这条曲线类似于“L”形状,其拐点所对应的正则化参数值即为选取的最优值。与其他正则化参数选取方法相比,L曲线法原理形象直观,计算简便。
2 传感层制备及修复本文采用的传感层制备材料为山东利特纳米科技有限公司生产的LN-GCI石墨烯导电碳油墨,其主要成分为碳油墨,掺入少量的石墨烯以提高其导电性。通过人工涂覆的方式,将其集成在混凝土表面,形成具有自感知性能的智能混凝土,通过电阻抗成像技术实现对混凝土结构损伤的监测识别。当智能传感层受到明显损伤后,再进行人工修复确保智能混凝土可以继续使用。
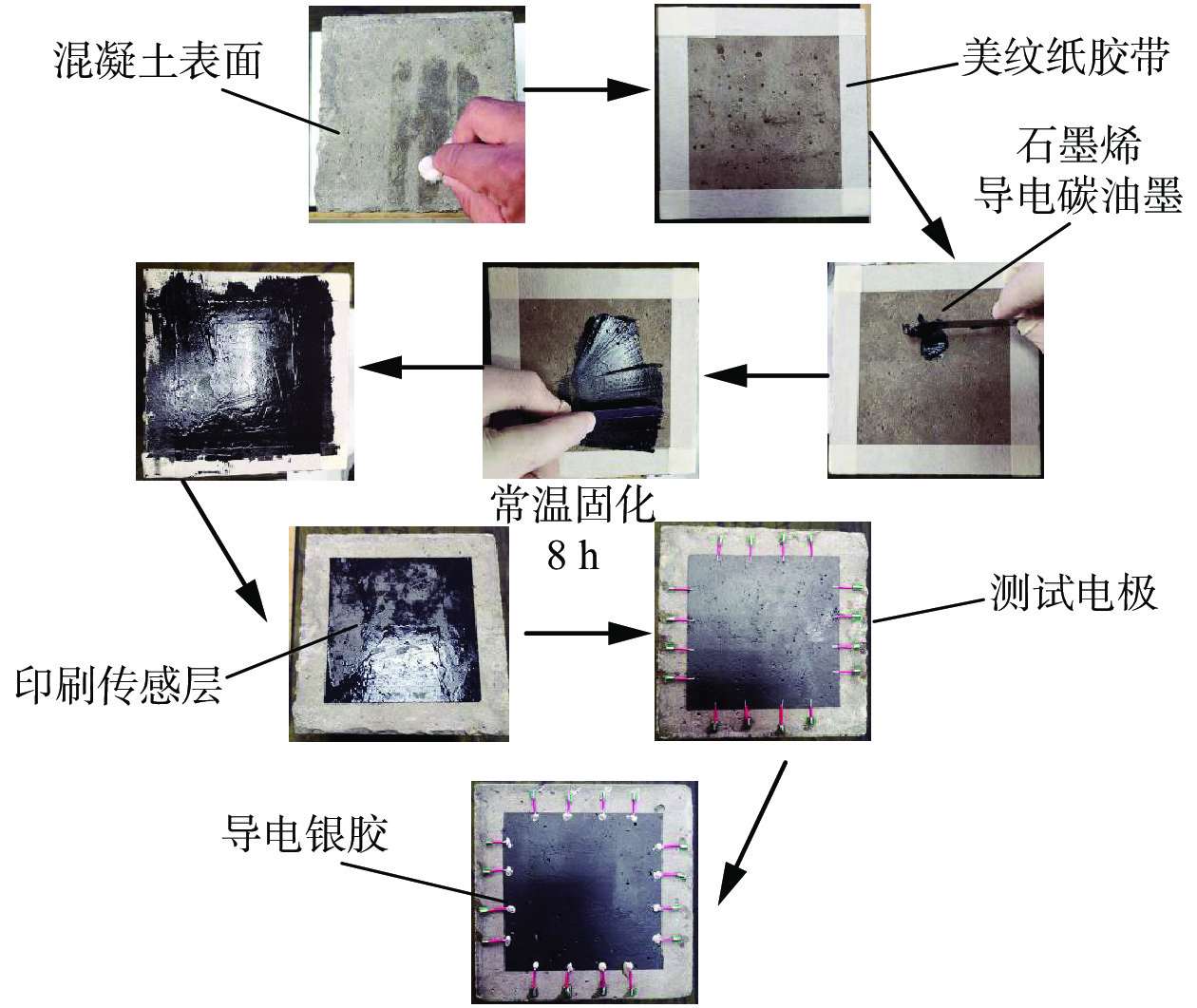
图1所示为所提出的自感知智能混凝土的制备流程:1)对混凝土基底进行砂纸打磨和酒精清理,保证混凝土表面的平整度和清洁度,使用美纹纸胶带布设测试所需的传感层区域;2)将石墨烯导电碳油墨倒入区域内,调整好刮刀的角度,运用刮刀使得油墨涂覆至整个区域,反复多次刮涂使得油墨层尽量均匀;3)涂覆完成后,收回多余油墨,去除美纹纸胶带布设的印版,得到预设传感层图案,在环境温度下固化8 h;4)根据电阻抗成像测试需要,在油墨传感层边缘指定位置,使用导电银浆布置一定数量的电极,使用热风枪加速电极固化,接着用导电银胶将细导线与电极相连,在环境温度下固化24 h;5)待电极完全固化后,测量相邻电极间电阻值,保证测点间通电性能良好。
|
| 图 1 自感知智能混凝土制备流程 |
自感知智能混凝土在使用过程中,一旦产生损伤,即会引起相应传感层损坏导致该区域电导率的扰动。损伤前后分别测试边界电压,根据电学成像重建算法进行数据处理,可以获得损伤引起的电导率变化分布图像,实现损伤识别并及时采取措施进行修复。在混凝土结构修复的基础上,对受损的传感层进行修复,以供后续感知使用。图2所示为修复智能传感层的过程,在传感层受损位置倒入适量的石墨烯导电碳油墨,调整刮刀角度往返多次刮涂,确保油墨印刷厚度均匀。修复的区域须全部覆盖受损范围,但不宜过大。回收多余油墨,使用热风枪对修复区域加速固化,热风的温度控制在80 ℃以下。

|
| 图 2 智能传感层修复图 |
3 损伤成像识别实验研究 3.1 电阻抗成像测试系统
本文通过实验研究来验证所提出技术和方法的有效性。为了保证测量精度,并考虑到仪器的便捷性,满足现场测试的需求,基于PXI平台集成了一套电学成像测试系统,如图3所示。该系统包括精密电源模块(NI-PXIe 4136)、高精度万用表模块(NI-PXIe 4081)、通道切换模块(NI-PXIe 2737)及控制器(NI-PXIe 8880)。配备了自主开发的电学成像测试软件,依照协议程序自动切换电极,在进行指定电极间的电流激励时,完成其他电极间的电压测量。

|
| 图 3 电学成像测试系统 |
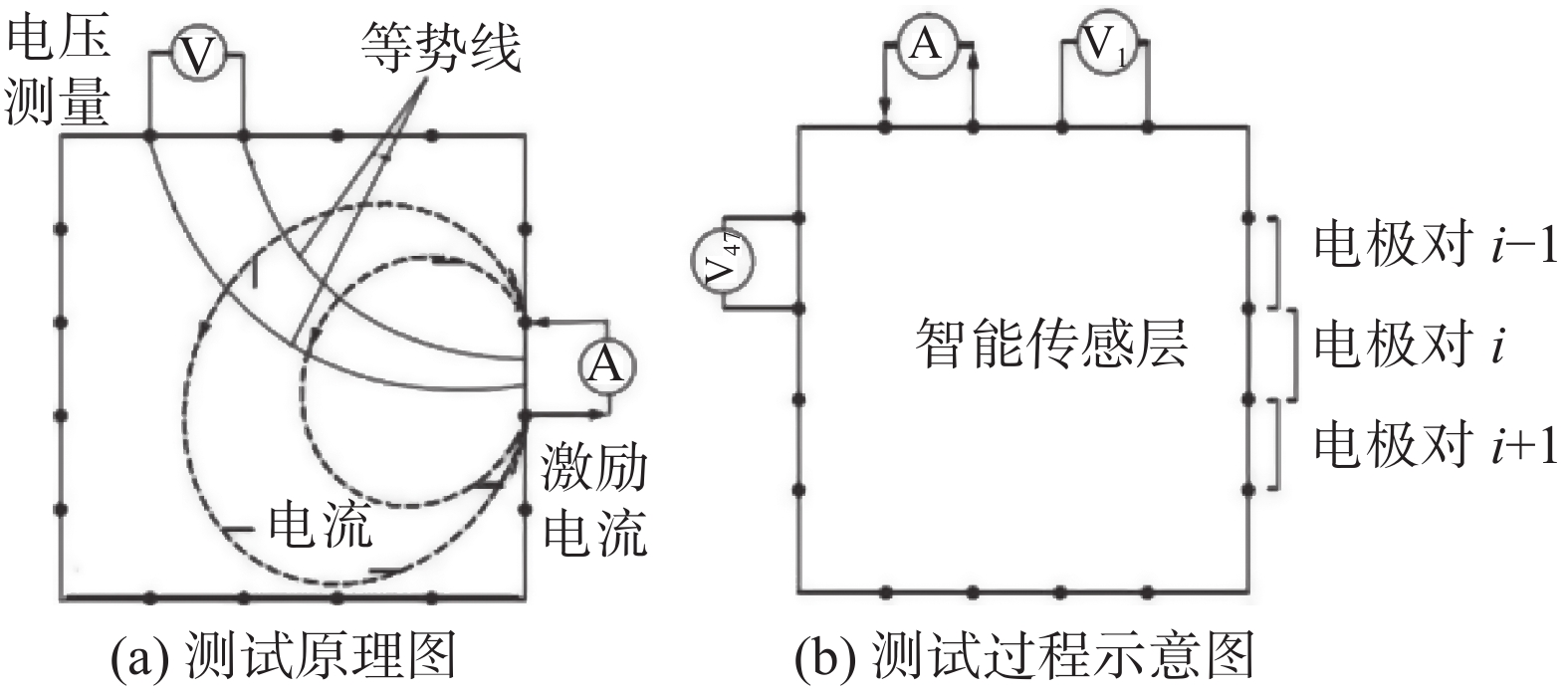
如图4所示,实验研究中共16(4×4)对相邻电极对,选用相邻电极模式的激励和测量方式,当1对相邻电极被电流激励时,测量与激励无关相邻电极间的电压值,总共测得208(16×13)个相邻边界电压值。根据电阻抗成像原理,首先测量智能传感层完好状态下的一组电压值作为基准参考值,激励电流大小为100 mA;然后当智能传感层受到不同程度损害时,分别测量不同损伤状态下的各组电压值;最后根据电阻抗成像算法对各组电压值进行数据处理,重建电导率分布状态并通过图像形式显示损伤信息和特征。
|
| 图 4 电阻抗成像测试原理及过程 |
3.2 损伤测试过程
实验研究中通过人工钻孔的方式在混凝土结构表面引入损伤,钻孔位置的混凝土损伤造成智能传感层的对应破坏,该区域电势场会发生相应的变化。如图5所示,在三个任意位置分别进行人工钻孔,孔径约为10 mm,依次造成混凝土结构表面的单损伤、双损伤和三损伤。

|
| 图 5 损伤情况 |
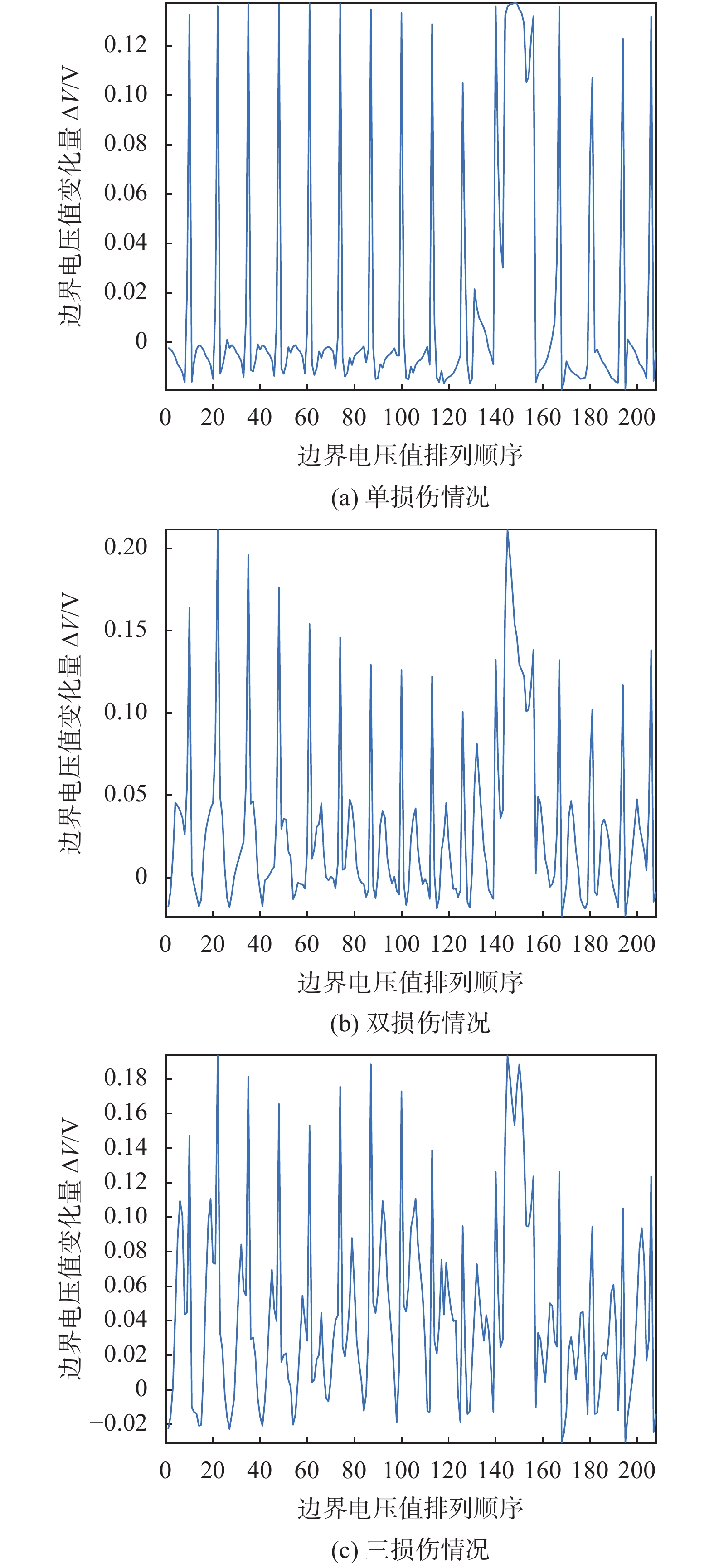
参照电阻抗成像原理的要求,利用电学成像测试系统分别测得四种情况(无损伤、单损伤、双损伤和三损伤)的传感层边界电压值。图6所示为三种损伤情况下与无损伤情况边界电压的归一化差值。从图中可以看出,与无损伤情况相比,由于损伤的发生,边界电压发生了明显的变化,不同个数及不同部位的损伤引起的边界电压信号变化具有不同的特征,但很难直接从信号变化中获取损伤信息,需要结合电阻抗成像模型,对其进行定量分析,确定并表征不同的损伤情况。
|
| 图 6 损伤前后边界电压差值 |
3.3 损伤成像识别结果
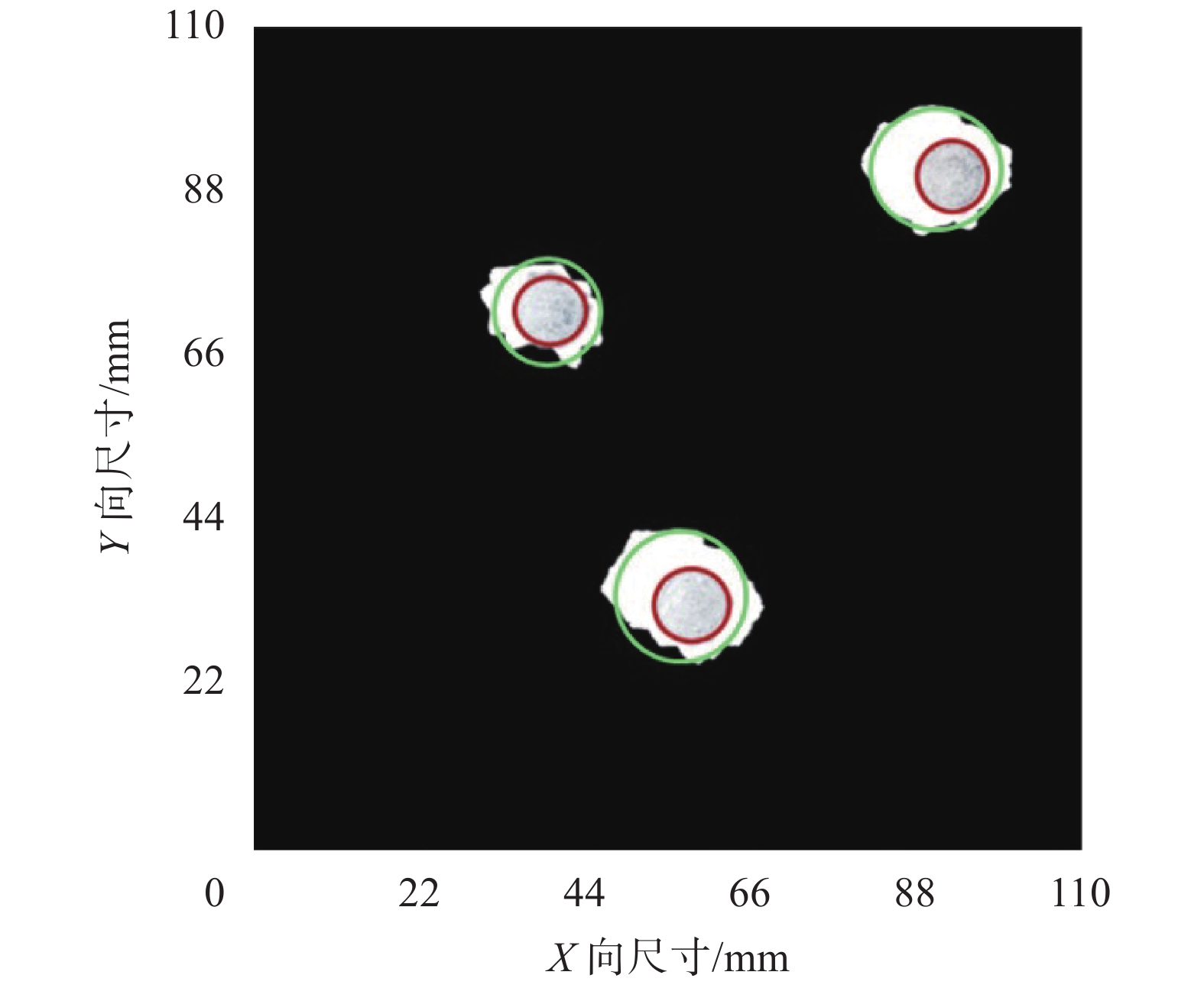
本文基于Tikhonov正则化算法对采集的边界电压值进行数据处理,通过比较损伤前后数据,获得由损伤所造成的电导率变化图。其中,最为关键的正则化参数采用L曲线法来选取,如图7所示为单损伤情况下的L曲线,其拐点所对应的参数即为选取的最优正则化参数。根据最优正则化参数,参照公式(8)重建电导率变化分布。通过图中不同颜色及深浅的区分,显示出一个、两个和三个区域的电导率变化,即为损伤区域,结果表明重建的电导率分布图像可以准确地反映损伤的数量、位置和大致形状等信息。图8所示分别为单损伤、双损伤和三损伤情况下重建的电导率分布图。在此基础上,对图8(c)三损伤重建图进行了二值化处理(取阈值为–0.25),并与混凝土实际损伤进行叠加处理,得到二值化处理与实损轮廓叠加图,并采用最小二乘算法将二值化处理的重建损伤拟合成圆曲线,如图9所示。可以看出,二值化处理图像更加直观反映了损伤信息,为进一步的定量对比分析提供了依据。表1给出了拟合的重建损伤和实际损伤坐标信息以及位置误差和尺寸误差,包括损伤中心位置坐标(xi, yi)、半径ri、圆心距误差ΔDi、面积误差ΔSi(i=1, 2, 3, 4, 5)(i=1, 2, 3为传感层修复前制作的三次损伤;i=4, 5为传感层修复后再次制造的二次损伤)。从图9和表1可以看出传感层修复前重建损伤的位置及面积和真实损伤情况较为接近,传感层修复后重建损伤的结果同修复前相比较误差更大,但基本反映了损伤的基本信息。传感层损伤后的修复不可避免造成涂层的分布不均以及厚度不同,而电阻抗成像分析模型是基于涂层分布均匀以及厚度一致,两者区别造成了修复后损伤识别精度下降,损伤的位置及面积误差显著增加。

|
| 图 7 L曲线法 |

|
| 图 8 智能混凝土损伤重建结果 |
|
| 图 9 二值化处理、拟合曲线与实损轮廓叠加图 |
| mm | ||||||||||||||
| 参数 | 损伤1 | 损伤2 | 损伤3 | 修复后
损伤4 |
修复后
损伤5 |
|||||||||
| (x1, y1) | r1 | (x2, y2) | r2 | (x3, y3) | r3 | (x4, y4) | (x5, y5) | r5 | ||||||
| 真实损伤 | (91,90) | 10 | (55,32) | 10 | (37,73) | 10 | (35,40) | 10 | (94,17) | 10 | ||||
| 重建损伤 | (90,90) | 16 | (54,33) | 17 | (37,73) | 14 | (38,39) | 23 | (89,20) | 26 | ||||
| 误差 | 0.5 | 256% | 1 | 289% | 0 | 196% | 2 | 529% | 4 | 676% | ||||
3.4 传感层修复实验结果
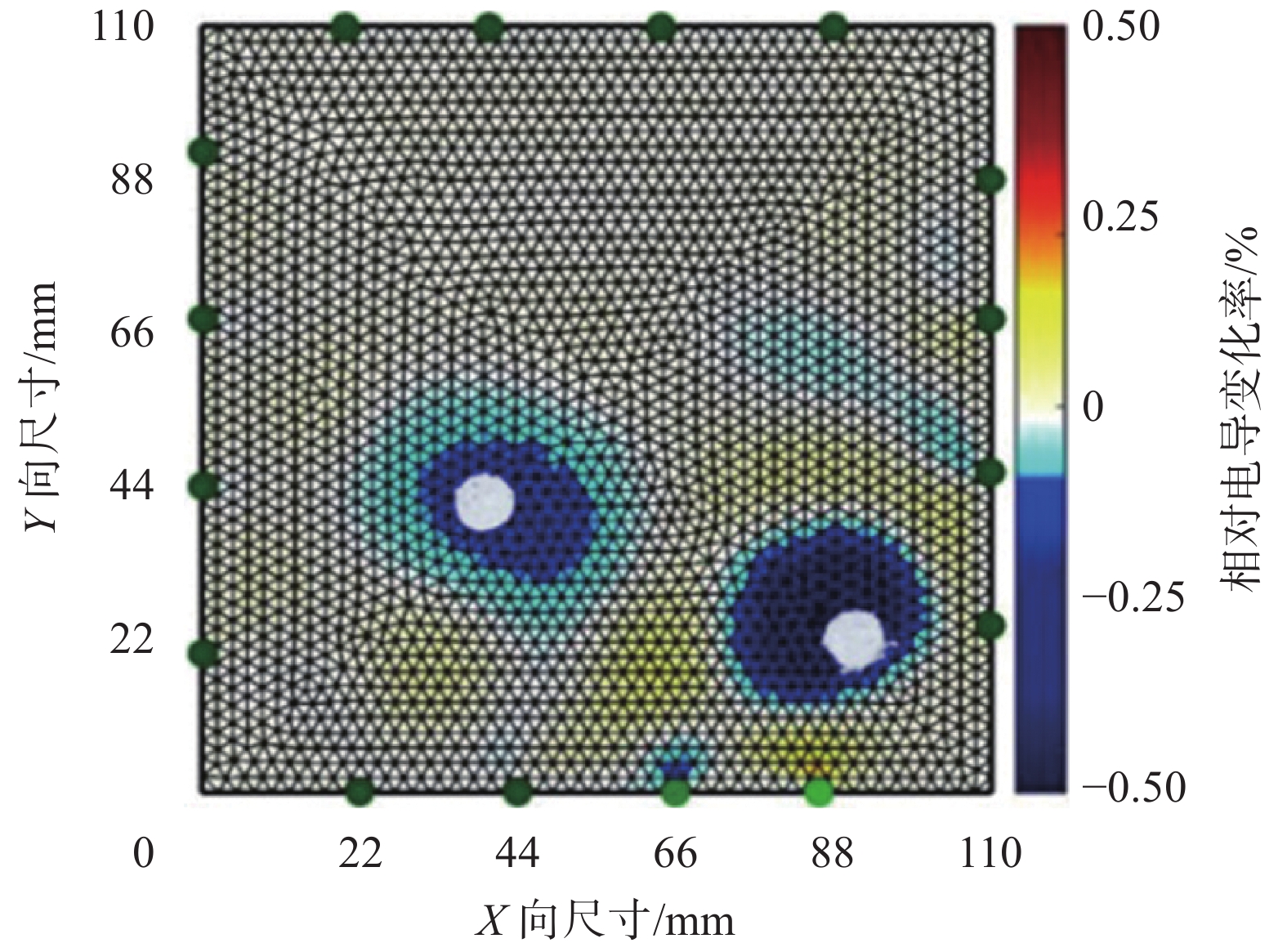
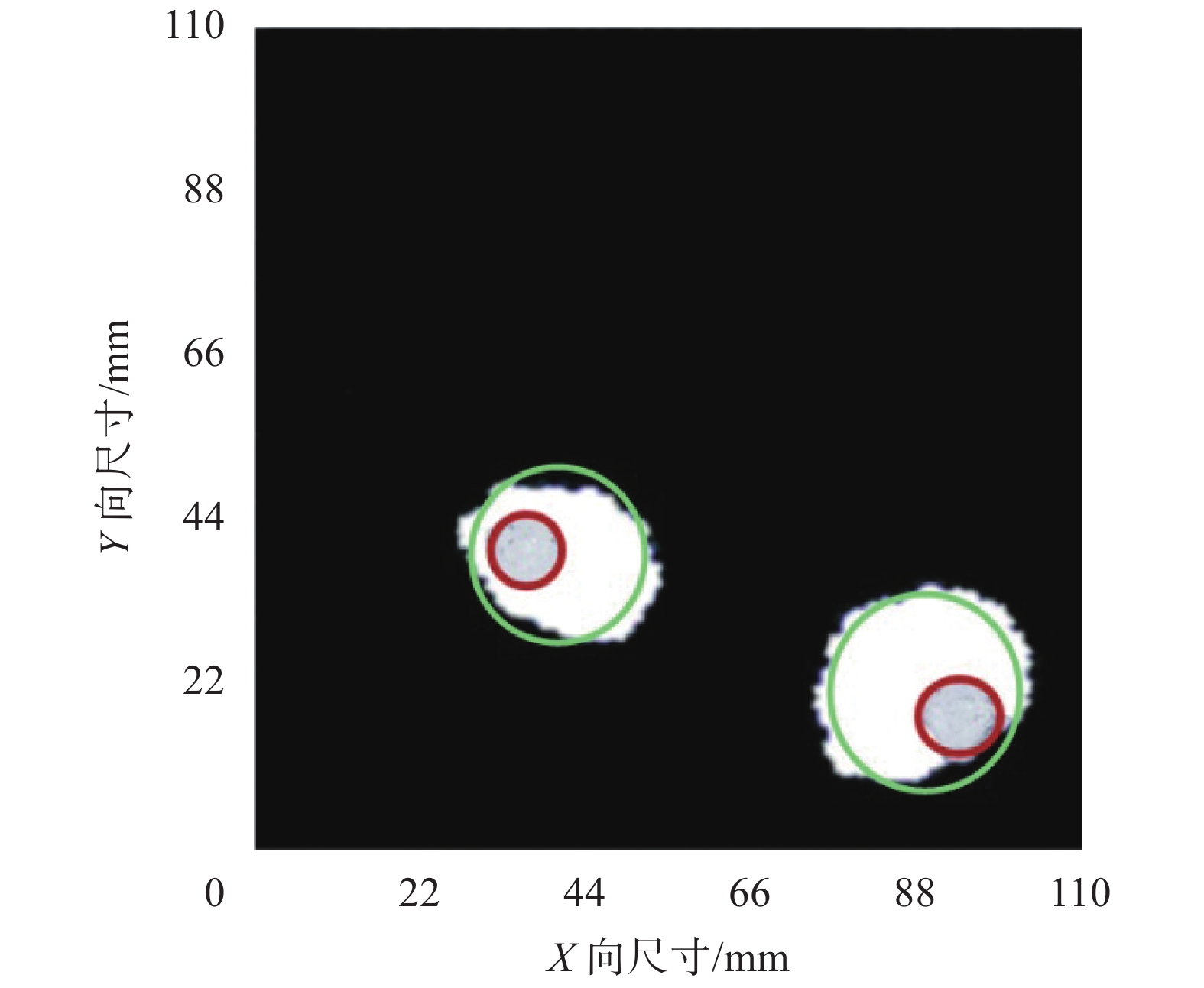
通过电阻抗成像技术检测出混凝土结构损伤后,首先对混凝土结构进行修复,接着采用图2所示方法对受损区域的印制传感层进行修复。待修复完毕后,通过钻孔的方式在混凝土结构表面制造区别于原先损伤位置的单损伤和双损伤,如图10所示。采用与3.1节相同的测试方法,获取修复后无损状态和损伤状态的边界电压值;并采用结合L曲线方法的Tikhonov正则化算法重建电导率变化图像。图11所示为修复后双损伤电导率变化重建图像结果。图12所示为取阈值为–0.25,对修复后的双损伤重建图进行二值化处理,并与实损轮廓进行叠加处理。由图可见,修复后的印制传感层的测试及重建结果与修复前相比,虽然在反映损伤位置,大小和形状方面结果有所欠缺,但是仍可以反映损伤的基本信息,可作为工程长期监测所用。

|
| 图 10 修复后的双损伤情况 |
|
| 图 11 修复后的双损伤重建结果图 |
|
| 图 12 二值化处理、拟合曲线与实损轮廓叠加图 |
4 结束语
本文采用石墨烯导电油墨作为功能材料,通过人工涂覆的方式将其集成在混凝土表面,制备成具有自感知功能的智能混凝土。基于电阻抗成像技术以及Tikhonov正则化算法,实现了混凝土表面损伤的监测和识别,重建结构损伤引起的传感层电导率变化分布图。在此基础上,对受损的智能传感层进行了修复,并采用相同的方法,重建新损伤的电导率变化分布图。根据上述原理,基于PXI平台集成了一套电学成像测试系统,并通过实验验证了所提出技术和方法的有效性。实验结果表明:1)采用石墨烯导电碳油墨制备的自感知智能混凝土对损伤进行监测是有效的,重建的电导率分布图像能够较好地反映损伤的数量、位置和形状尺寸;2)通过人工方式修复受损传感层的方法是可行的,通过不断地修复,可以实现对混凝土结构全寿命使用过程进行长期持续监测。
| [1] |
叶青, 程智, 胡小红, 等. 基于雷达波相位干涉技术的杆塔结构形变监测研究[J].
中国测试, 2021(9): 34-40.
DOI:10.11857/j.issn.1674-5124.2020100121 |
| [2] |
NEGI P, CHHABRA R, KAUR N, et al. Health monitoring of reinforced concrete structures under impact using multiple piezo-based configurations[J].
Construction and Building Materials, 2019, 222: 371-389.
DOI:10.1016/j.conbuildmat.2019.06.100 |
| [3] |
KARHUNEN K, SEPPANEN A, LEHIKOINEN A, et al. Electrical resistance tomography imaging of concrete[J].
Cement and Concrete Research, 2010, 40(1): 137-145.
DOI:10.1016/j.cemconres.2009.08.023 |
| [4] |
REN H, TIAN K, HONG S, et al. Visualized investigation of defect in cementitious materials with electrical resistance tomography[J].
Construction and Building Materials, 2019, 196: 428-436.
DOI:10.1016/j.conbuildmat.2018.11.129 |
| [5] |
余佳干, 陈智俊, 周小勇, 等. 混凝土缺陷检测的电阻成像约束反问题算法优化[J].
重庆大学学报, 2019, 42(5): 66-75.
DOI:10.11835/j.issn.1000-582X.2019.05.008 |
| [6] |
HAN B, WANG Y, DONG S, et al. Smart concretes and structures: a review[J].
Journal of Intelligent Material Systemsand Structures, 2015, 26(11): 1303-1345.
DOI:10.1177/1045389X15586452 |
| [7] |
PIERRE-CLAUDE A. Cements of yesterday and today: concrete of tomorrow[J].
Cement and Concrete Research, 2000, 30(9): 1349-1359.
DOI:10.1016/S0008-8846(00)00365-3 |
| [8] |
HALLAJI M, SEPPANEN A, POUR-GHAZ M. Electrical impedance tomography-based sensing skin for quantitative imaging of damage in concrete[J].
Smart Materials and Structures, 2014, 23: 085001.
DOI:10.1088/0964-1726/23/8/085001 |
| [9] |
SEPPANEN A, HALLAJI M, POUR-GHAZ M. A functionally layered sensing skin for the detection of corrosive elements and cracking[J].
Structural Health Monitoring, 2017, 16(2): 215-224.
DOI:10.1177/1475921716670574 |
| [10] |
DOWNEY A, D’ALESSANDRO A, UBERTINI F, et al. Automated crack detection in conductive smartconcrete structures using a resistor mesh model[J].
Measurement Science and Technology, 2018, 29: 035107.
DOI:10.1088/1361-6501/aa9fb8 |
| [11] |
ZYMELKA D, YAMASHITA T, TAKAMATSU S, et al. Thin-film flexible sensor for omnidirectional strain measurements[J].
Sensors and Actuators A:Physical, 2017, 263: 391-397.
DOI:10.1016/j.sna.2017.05.040 |
| [12] |
YAN G, ZHENG Y. A printed electrical impedance tomography sensor for detection of damage in composites[J].
International Journal of Applied Electromagnetics and Mechanics, 2020, 64: 1011-1017.
DOI:10.3233/JAE-209416 |
| [13] |
VAUHKONEN M. Electrical impedance tomography and prior information[D]. Kuopio: University of Kuopio, 1997.
|
| [14] |
刘继军. 不适定问题的正则化方法及应用[M]. 北京: 科学出版社, 2005.
|
| [15] |
CALVETTI D, MORIGI S, REICHEL L, et al. Tikhonov regularization and the L-curve for large discrete ill-posed problems[J].
Journal of Computational and Applied Mathematics, 2000, 123(1-2): 423-446.
DOI:10.1016/S0377-0427(00)00414-3 |
 2022, Vol. 48
2022, Vol. 48


 ,
,