0 引　言

随着我国经济迅速发展，交通运输量也急剧增加，超载愈加严重。车辆动态称重系统是治理超载超限一个有效手段，并且随着技术的进步，可以有效地解决省界收费站取消后的超限超载难治理的问题，但如何提高称重精度仍是系统发展的重点和核心^[1-2]。其中一个难点是在路面激励、车速、车辆振动等因素的影响下，将称重传感器采集到的真实信号分离出来^[3]。宋文凤^[4]提出了加权-滑动平均滤波组合算法对信号处理，杨军^[5]利用卡尔曼滤波算法滤除周期性干扰信号效果明显，但以上算法应对偶然出现的脉冲性干扰的抑制效果不佳，车辆高速状态下效果差。另一个核心是建立合适的称重模型进行校正。陈超波^[6]通过构建RBF神经网络（radial basis function neural network）动态称重模型对车重进行拟合，有效降低了称重误差。王春香^[7]利用基于遗传算法的多段曲线拟合车重，滤除了低速干扰信号的影响。郝晓娴^[8]通过建立BP神经网络称重模型提高了处理精度。上述模型在实际应用中仍存在许多不足，如最小二乘法拟合仅适用于低速，神经网络法收敛慢、迭代数多、易陷入局部最小和全局搜索能力不足等缺点。

针对上述算法及模型的不足，本文从减少噪声干扰及提高动态称重精度出发，利用小波变换对称重信号进行滤波及信号重构。针对神经网络收敛速度慢、易陷入局部极值的问题，提出了遗传算法结合粒子群算法对神经网络进行优化的动态称重模型，通过滤波算法预处理及建立称重模型校正，实现对车辆动态称重信号的高精度处理。

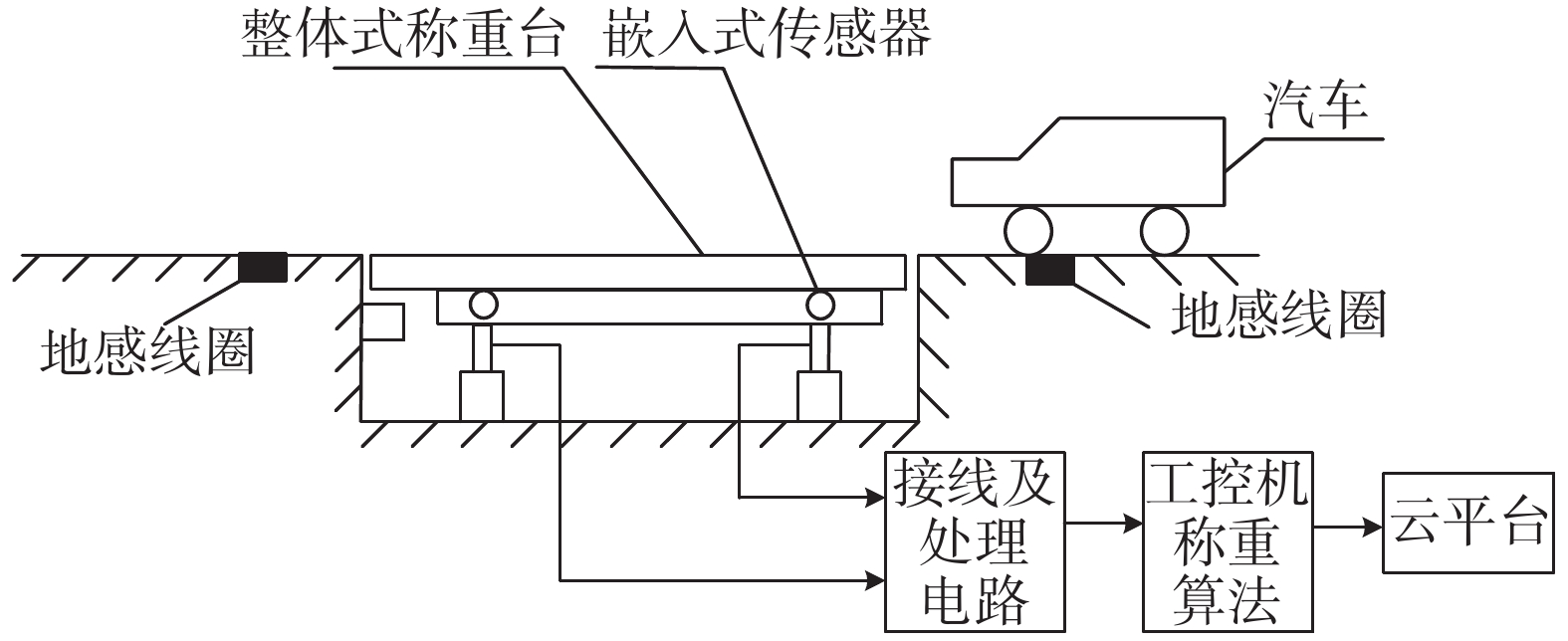
1 动态称重系统的结构及原理

动态称重系统主要由工型主梁一体化秤台、嵌入式应变传感器、信号处理电路、地感线圈、工控机、云平台等部分组成，图1为动态称重系统的结构图^[9]。动态称重系统首先将焊接好的秤台与公路采用高强度混凝土浇筑连接，秤台平面与路面水平，使称重设备与公路之间同平面无间隙。垂直行车方向的单个工型梁上安装两个嵌入式应变传感器。当车辆行驶经过称台时，秤台上承受的压力导致结构梁及应变片发生形变，将质量信号转换为差分信号；信号处理电路将传感器传来的信号进行放大、滤波处理；工控机对电压信号进一步处理运算得到车辆修正后的动态质量，并将处理结果上传至云平台。

2 动态称重信号预处理

动态称重信号中包含着各种噪声，可以分为低频随机振动噪声干扰和高频噪声干扰^[10]，动态称重信号主要表现为低频信号，影响称量精度的最主要因素是高频噪声。

车辆通过秤台产生的理想波形为梯形波，梯形波的上底表示为车辆驶过秤台的波形，实际的波形受车速、车辆振动、路面激励、环境等因素影响，因此想要提高动态称重精度，首先需要对信号进行去噪处理，使采集波形接近理想波形^[11]。

Daubechies小波函数（简称dbN小波，N是小波的阶数）对不规则信号较为敏感，在信号分析上应用广泛^[12]，db4小波为紧支撑正交实小波，正交性好、消失矩大，在时频域分析中优势明显，为了获得被干扰信号淹没的真实动态称重信号，可以利用db4小波对称重信号进行多层分解并重构，减小噪声信号的干扰。除N=1（Harr小波）外，dbN没有明确的公式表达，小波函数 $\psi \left( t \right)$ 可以由尺度函数 $\phi \left( t \right)$ 以及滤波器系数 ${g_k}$ 求出， $\psi \left( t \right)$ 是 $\phi \left( {{{2t}}} \right)$ 的位移加权和，公式如下：

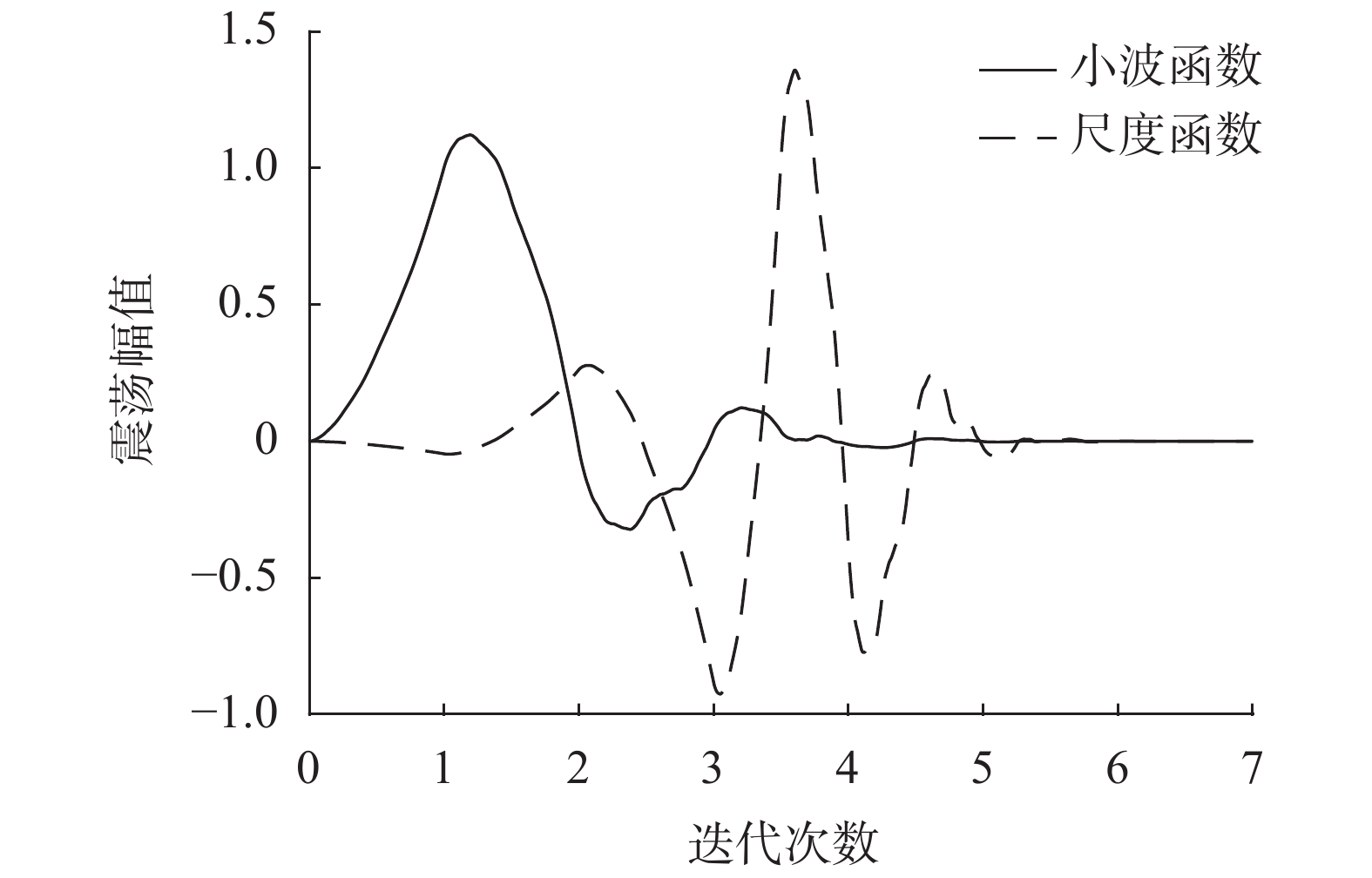
db4小波函数和尺度函数如图2所示。

设连续函数 $f(x) \in {L^2}(R)$ ，则 $f\left( x \right)$ 以db4作为基本小波的连续小波变换为：

式中：a——伸缩因子；

b——平移因子；

$\overline \psi \left( {{x}} \right)$ —— $\psi \left( {{x}} \right)$ 的复共轭复数。

取 ${a_0} > 0$ ， ${b_0} > 0$ ， $a = a_0^m$ ， $b = b_0^m$ 则其对应的高离散小波变换：

式中， $t$ 为离散时间参数，m为伸缩因子，n为平移因子；通常选取 ${a_0} = {b_0} = 2$ ，其对应的变换为二进制离散小波变换。

选取不同的m值对应着不同的带通滤波器 $\psi \left( \omega \right)$ ，从而分离出不同频率的称重信号及噪声，进而得真实动态车重信号。小波分解步骤^[13]如下：

1）确定小波类型及小波分解的层次。

2）高频系数阈值选择。选择第一层到第N层的阈值。

3）根据第N层的低频系数和第一层到第N层的高频系数，对信号进行分解和重构。

4）本文采用db4小波分解函数对信号进行5层分解：

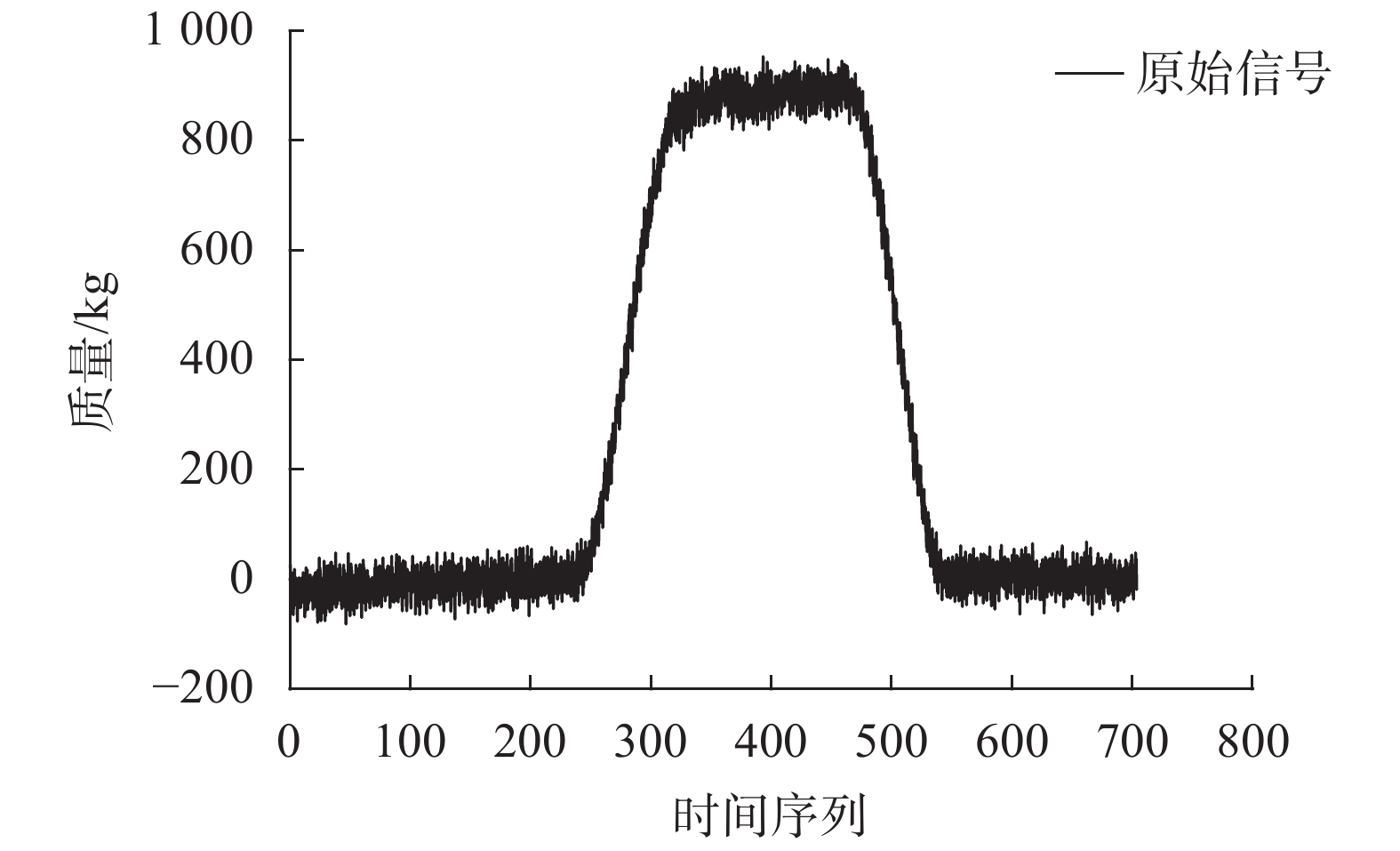
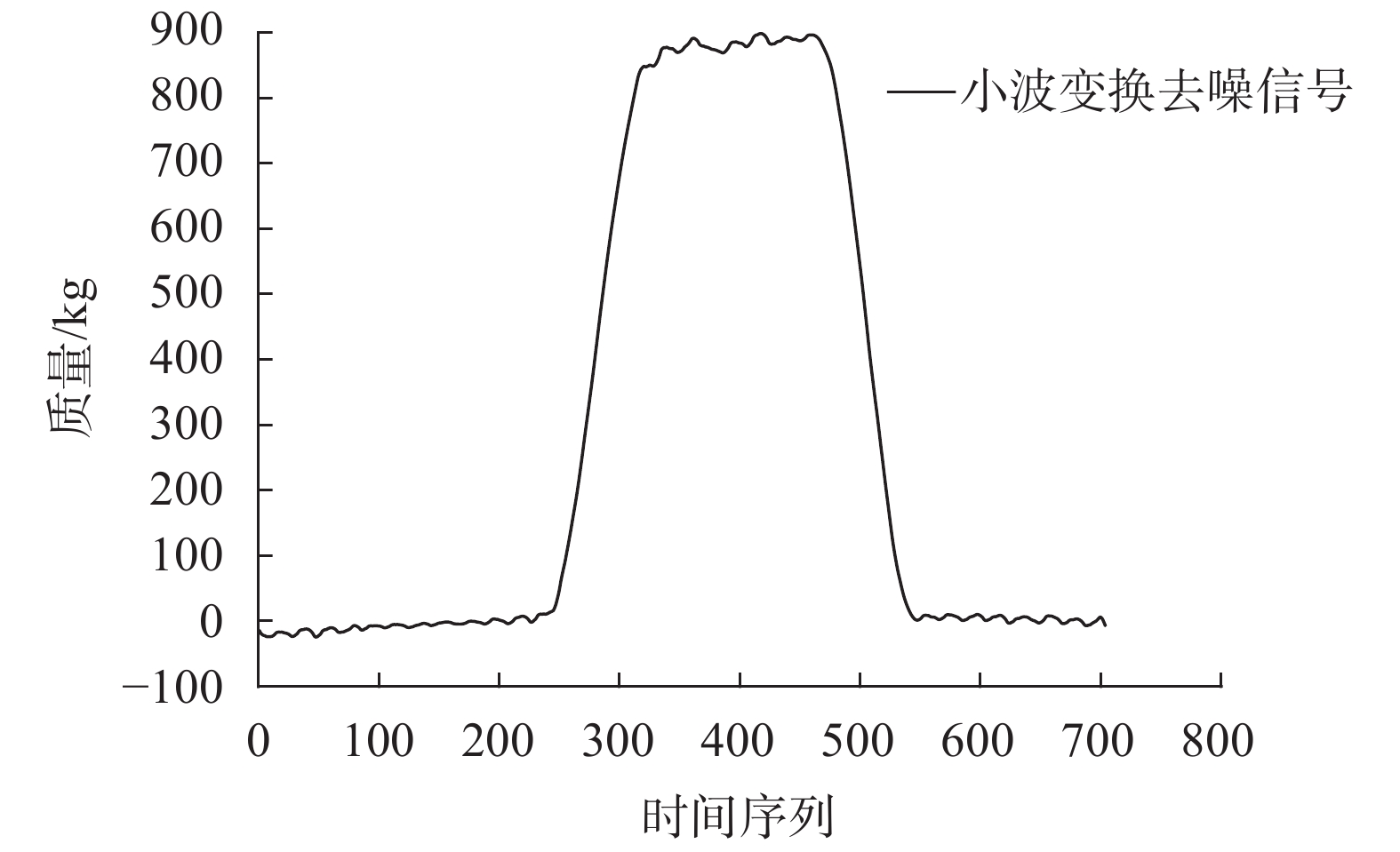
其中wavedec是一个小波分解函数，x5为被分解的函数，5表示分解的层数，db4表示采用的小波分解函数。图3和图4分别表示为对信号进行去噪重构前、重构后的结果。通过小波变换去噪重构的信号波形更接近于理想信号，保证了动态车重获取的准确性及称重模型建立可靠性。

3 动态称重模型及算法 3.1 GA-PSO算法

粒子群算法是一种并行随机搜索的算法，在个体适应度条件下进行全局搜索，迭代更新每一个粒子的速度和位置，并保存个体和集体极值，能短时间内精准接近目标，但寻优过程中易陷入局部极值。遗传算法同粒子群算法类似，都是基于种群及种群适应度。遗传算法具有良好的并行计算能力和全局搜索能力，但在种群迭代更新中存在信息丢失，并不会将个体的信息进行保存，易出现收敛缓慢或停止的现象^[14]。针对两种算法的缺陷，本文将遗传算法中交叉、变异操作引入粒子群算法完成对粒子进行更新，使算法具备了遗传算法全局收敛和粒子群算法收敛速度快的优点。

PSO算法寻优是每个粒子在迭代过程中对其速度和位置进行更新：

式中： $k$ ——进化代数；

$\omega $ ——惯性权系数；

${c_1},{c_2}$ ——学习因子；

${r_1},{r_2}$ ——[0,1]间的随机数。

为了防止在迭代过程中粒子运动范围过大或速度太快，还需要设置参数对粒子的位置和速度进行更新并加以限制。

混合算法中首先更新粒子的速度项，不再利用惯性系数乘以原始速度，而是将粒子速度进行变异操作，用遗传算法的变异概率 ${P_{\rm m}}$ 替换速度项 $\omega {V_i}\left( k \right)$ ，然后让粒子分别先后与个体极值、全局极值进行交叉操作，用遗传算法的交叉概率 ${P_{\rm c}}$ 进行替换。最后将经过遗传处理的粒子及其对应的速度项相加，完成粒子的更新。

3.2 GA-PSO算法优化BP神经网络

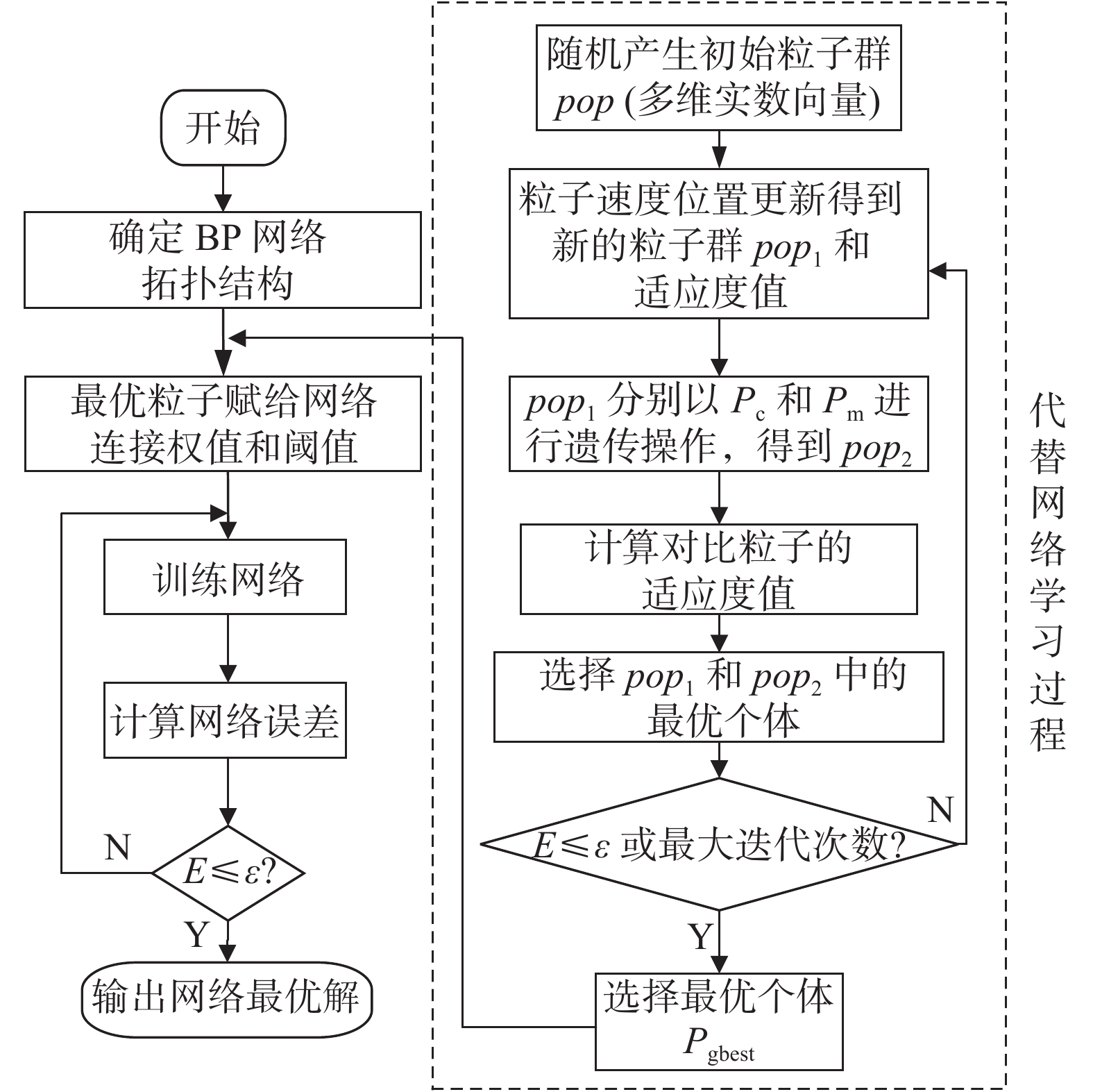
GA-PSO算法能够有效地克服BP算法的局部最优的缺陷，迭代优化网络的权值和阈值^[15]，GA-PSO-BP的算法流程（见图5）如下：

1）初始化神经网络。确定BP神经网络的网络结构及基本参数。

2）初始化种群。根据网络结构确定种群的规模 $R$ 、维度 $D$ 、每个粒子的速度 $v$ 、位置 $p$ 。以BP神经网络的误差函数 $E\left( \omega \right)$ 作为适应度值函数，评价各粒子的质量：

式中： $l$ ——输出节点数；

${y_i}$ 、 ${o_i}$ ——期望输出和预测输出。

3）粒子群的迭代。计算更新粒子的速度和位置及粒子的适应度，得到新种群 $po{p_1}$ 。

4）粒子群的遗传操作。新种群 $po{p_1}$ 中的粒子先后以交叉概率 ${P_{\rm c}}$ 与个体极值粒子和全局极值粒子进行交叉，再对适应度值差的粒子以 ${P_{\rm m}}$ 的变异概率进行随机初始化。

5）更新粒子的最优适应度函数值、最优位置 ${P_{\rm ibest}}$ 和 ${P_{\rm gbest}}$ ，替换上一代的遗传优化的最优粒子。

6）判断粒子群迭代次数会否大于最大迭代数，或者适应度函数的值是否优于前一代，以最优个体值作为神经网络参数。

4 算法处理与结果分析 4.1 实验数据获取

2019年10月至12月在浙江某汽车动态称重设备测试现场进行了设备布置，对车辆动态情况下的称重系统进行了实验测试。

实验前对6辆车进行静态标定，获取车辆的静态车重。测试并记录各车辆通过秤台的动态车辆速度及轴数，试验车辆如表1所示：选取二轴、四轴、六轴货车各2辆，总共6种不同载荷，实验总共采集数据189组。

4.2 动态称重模型建立及参数选择

选取车辆动态称重拟合值作为神经网络输出，预处理后的动态车重、车速、车辆轴数作为BP网络输入，进行训练。本实验中PSO种群规模 $R = $ $ 100$ ，粒子维度D=36， ${c_1} = {c_2} = 2$ ，收敛精度 $E = 0.001$ ，遗传算法交叉概率 ${P_{\rm c}} = 0.7$ ，变异概率 ${P_{\rm m}} = 0.2$ 。BP网络输入节点数为3，隐含层节点数为5，输出节点数为1，训练次数设置为1000，学习速率设置为0.1，目标误差为0.0001。每种车型随机挑选两个样本，共选取12组样本作为测试数据，剩下的177组数据作为训练样本进行模型训练。

首先通过mapminmax函数对输入输出数据进行归一化和反归一化处理，提高样本的收敛速度，选择学习效率高且迭代误差减小幅度较大的trainlm函数作为学习函数，误差较小的tansig正切函数作为输入层到隐含层传递函数，purelin线性函数作为隐含层到输出层的传递函数。

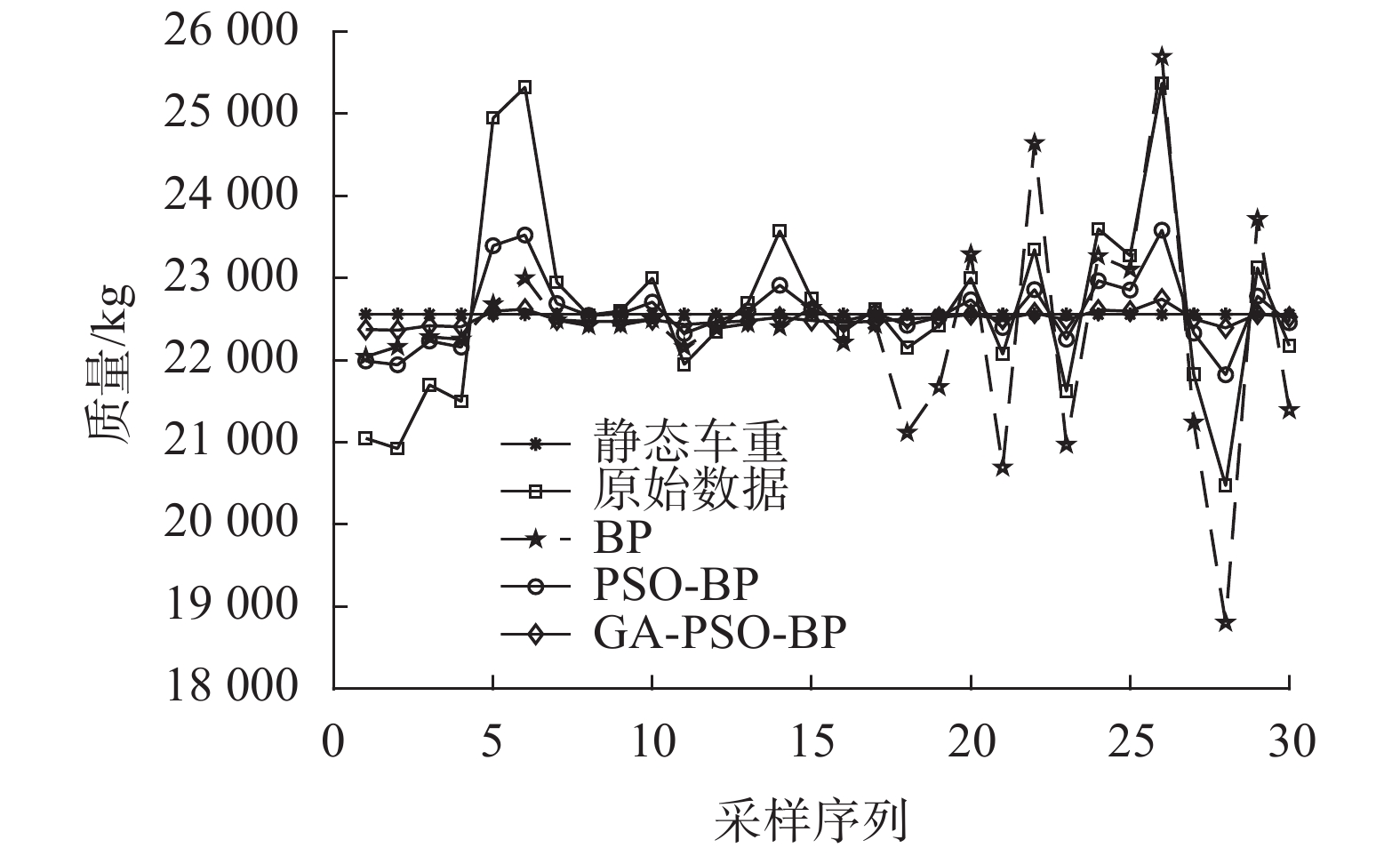
4.3 实验及结果分析

实验以静态质量为22560 kg的四轴货车为例，构建GA-PSO-BP称重模型，并与BP模型、PSO-BP模型及静态车重、原始数据进行对比分析，如图6所示。在各拟合曲线中，BP、PSO-BP称重模型由于易陷入局部最优解的缺陷，与静态车重的值相差较大，从GA-PSO-BP模型的拟合曲线来看通过GA和PSO模型的优势互补，预测值与静态车重能够较好地吻合。

PSO-BP神经网络适应度函数值和GA-PSO-BP神经网络的适应度函数值如图7所示，混合算法优化的网络模型收敛速度和最优个体适应度值都好于PSO-BP模型，经过100代的迭代，GA-PSO-BP的最优个体适应度函数值为0.0501，PSO-BP得到的适应度函数值为0.7358。

为验证训练完成的GA-PSO-BP神经网络验证动态称重模型的准确性及优越性，将选取的12组测试样本用于验证，由表2可知，最大称重误差降至0.9849%，称重结果满足JJG 907—2006《车辆自动衡器检定规程》中1级秤的规定误差不超过1%的要求。

5 结束语

本文提出了一种基于小波变换和GA-PSO-BP神经网络动态称重模型。通过对信号的滤波重构，降低了复杂环境对真实称重信号获取的影响。融合粒子群算法全局寻优及遗传算法的并行计算的优点，有效克服了BP神经网络易陷入局部极值的问题，提高了收敛速度，并用训练好的网络对称重数据进行了验证。实验结果表明，模型所需样本少，精度高，能有效地将车辆的称重误差控制在1%以内，称重结果达到国标JJG907—2006《车辆自动衡器检定规程》中的1级标准。该方法的应用可以为解决省界收费站取消以后的治理超限超载提供有效助力。