文章信息
- 高继勋, 黄全振, 赵媛媛
- GAO Jixun, HUANG Quanzhen, ZHAO Yuanyuan
- 基于领航跟随的多机器人编队控制方法
- Multi robot formation control based on leader-follower method
- 中国测试, 2021, 47(11): 8-13
- CHINA MEASUREMENT & TEST, 2021, 47(11): 8-13
- http://dx.doi.org/10.11857/j.issn.1674-5124.2021060043
-
文章历史
- 收稿日期: 2021-06-10
- 收到修改稿日期: 2021-07-20
2. 河南工程学院电气信息学院,河南 郑州 451191;
3. 郑州工程技术学院,河南 郑州450044
2. School of Electrical Information Engineering, Henan University of Engineering, Zhengzhou 451191, China;
3. Zhengzhou University of Technology, Zhengzhou 450044, China
随着人工智能时代的到来,多机器人的控制已逐渐成为研究热点[1-6],其应用场景包括但不限于农业、军事、航空等领域。在多机器人编队的协同控制过程中,通常所期望队形是可变的,以便于应对单个机器人无法完成的复杂任务。在极坐标下,利用线性反馈的方法建立“距离-角度”控制器模型,完成对多机器人编队控制[7]。由于奇异点存在,该控制器存在一定问题。可通过将极坐标投影到笛卡尔坐标系下,重新建立控制模型解决奇异点问题[8-9]。钟宜生等[10]提出,将多机器人可变编队问题描述为“不变的队形在可变的坐标系中运动”的编队控制问题。在上述基础上,李清东[11]提出用多个不变队形互相切换,以完成编队控制。刘磊[12]采用以差速轮式机器人为研究对象,通过仿真验证该控制方法的可行性。
目前对于解决多机器人一般性编队控制问题,公开文献中尚未见到成熟方案。现阶段主要有人工势场法[13]、基于行为法[14]、虚拟结构法[15]和领航-跟随法[16]。上述方法各有其优缺点,相比较而言,领航-跟随法的控制更简单,只需调整跟随者与领航者的运动参数即可完成跟踪控制,具有较好的稳定性和灵活性[17-20]。
根据上述情况,本文提出了一种新颖的机器人编队控制方法,该方法基于领航-跟随法,引入“虚拟领航机器人”,将其他机器人作为跟随者,建立控制模型,从而将编队问题转化为跟踪控制问题。根据提出的控制算法,本文设计了跟随误差控制器,分析跟随误差及其收敛性。通过仿真与实验结果分析,验证本文提出的改进型领航-跟随控制方法在一致性控制中的有效性与稳定性。
1 问题描述和模型构建 1.1 问题描述基于领航-跟随法,可将编队问题转化为跟随机器人对虚拟领航机器人的轨迹跟踪,该方法只需获得虚拟领航者的运动参数和位姿即可实现跟踪控制,一定程度上减少相互之间信息冗余及计算量。通过上述方法,建立虚拟领航机器人与跟随机器人运动模型,如图1所示。

|
| 图 1 领航-跟随结构示意图 |
图中,跟随机器人R1与虚拟领航机器人R0的距离是
非完整移动机器人的运动学模型[15]如下式:
| $ \dot {\boldsymbol{q}} = {\boldsymbol{S}}({\boldsymbol{q}}){\boldsymbol{u}} $ | (1) |
| $ \dot {\boldsymbol{u}} = {\boldsymbol{a}} $ | (2) |
其中,
由图1可知,当跟随机器人R1与虚拟领航机器人R0之间的位姿(位置和姿态)误差趋近于零,即:
| $ \mathop{{\rm{lim}}}\limits_{t \to \infty } ({{\boldsymbol{Q}}_0} - {{\boldsymbol{Q}}_1}) = {{0}} $ | (3) |
其中
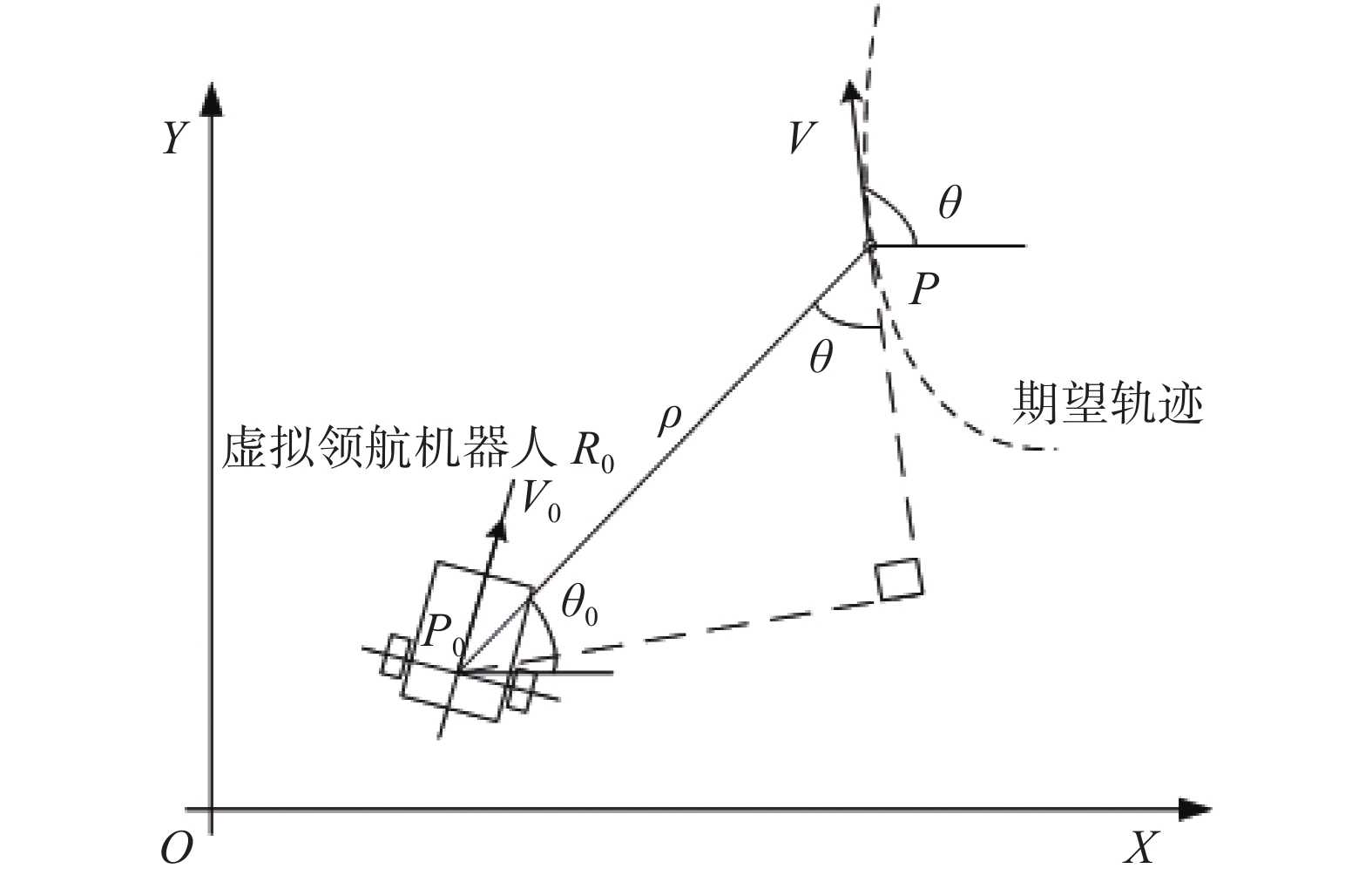
假设在t时刻,虚拟领航机器人与期望轨迹运动示意图如图2所示。
|
| 图 2 跟踪位置示意图 |
其中,V为期望轨迹上P点的运动方向,与X轴正方向夹角为θ。P0P为虚拟领航机器人与期望轨迹上P点的连线。P点状态表示为(X , Y , θ)。
虚拟领航机器人与期望轨迹误差参数表示为:
| $ {\boldsymbol{\lambda}} = {\left[ {{{\rho}} _0'\; {{\theta}} _0'} \right]^{\rm T}} $ | (4) |
式中:
通过对参数
虚拟领航机器人运动学模型可表示为:
| $ {\dot {\boldsymbol{Q}}_0} = \left[ {\begin{array}{*{20}{c}} {{{\dot {{X}}}_0}} \\ {{{\dot {{Y}}}_0}} \\ {{{\dot {{\theta}} }_0}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{cos}}{{{\theta}} _0}}&0 \\ {{\rm{sin}}{{{\theta}} _0}}&0 \\ 0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{V}}_0}} \\ {{{{W}}_0}} \end{array}} \right] $ | (5) |
跟随机器人参考轨迹模型为:
| $ \left\{ {\begin{array}{*{20}{l}} {{{\dot {{X}}}_1} = {{{V}}_1}{\rm{cos}}{{{\theta}} _1}} \\ {{{\dot {{Y}}}_1} = {{{V}}_1}{\rm{sin}}{{{\theta}} _1}} \\ {{{\dot {{\theta}} }_1} = {{{W}}_1}} \end{array}} \right. $ | (6) |
根据期望轨迹P点状态及公式(4)可得到虚拟领航机器人位姿,其数学表达式如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{{{X}}_0} = {{X}} - {{\rho}} _0'\sin \left({{\theta}} _0' - {{\theta}} + \dfrac{\pi}{2}\right)} \\ {{{{Y}}_0} = {{Y}} - {{\rho}} _0'\cos \left({{\theta}} _0' - {{\theta}} + \dfrac{\pi}{2}\right)} \\ {{{{\theta}} _0} = {{\theta}} - {{\theta}} _0'} \end{array}} \right. $ | (7) |
跟随机器人R1与虚拟领航机器人R0位姿误差为
| $ {{{\boldsymbol e}}_i} = \left[ {\begin{array}{*{20}{c}} {{{{e}}_{i1}}} \\ {{{{e}}_{i2}}} \\ {{{{e}}_{i3}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {\cos {{{\theta}}_1}}&{\sin {{{\theta}}_1}}&0 \\ { - \sin {{{\theta}}_1}}&{\cos {{{\theta}}_1}}&0 \\ 0&0&1 \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{{{X}}_0} - {{{X}}_1}} \\ {{{{Y}}_0} - {{{Y}}_1}} \\ {{{{\theta}}_0} - {{{\theta}}_1}} \end{array}} \right] $ | (8) |
对于跟随机器人R1,速度控制输入
| $ {{\boldsymbol{u}}_1} = \left[ {\begin{array}{*{20}{c}} {{{{V}}_0}{\rm{cos}}{{{e}}_{i3}} + {{{K}}_1}{{{e}}_{i1}}} \\ {{{{W}}_0} + {{{V}}_0}({{{K}}_2}{{{e}}_{i2}} + {{{K}}_3}{\rm{sin}}{{{e}}_{i3}})} \end{array}} \right] $ | (9) |
其中,K1,K2,K3为正数。
定义Lyapunov函数
| $ {{{V}}_{{\rm L}}} = \frac{1}{2}{{e}}_{i1}^2 + \frac{1}{2}{{e}}_{i2}^2 + \frac{{1 - {\rm{cos}}{{{e}}_{i3}}}}{{{{{K}}_2}}} $ | (10) |
则,
| $ {\dot {{V}}_{\rm{L}}} = {{{e}}_{i1}}{\dot {{e}}_{i1}} + {{{e}}_{i2}}{\dot {{e}}_{i2}} + {\dot {{e}}_{i3}}\frac{{{\rm{sin}}{{{e}}_{i3}}}}{{{{{K}}_2}}} = - {{{K}}_1}{{e}}_{i1}^2 - \frac{{{{{K}}_3}{\rm{si}}{{\rm{n}}^2}{{{e}}_{i3}}}}{{{{{K}}_2}}} $ | (11) |
由公式(10)和(11)可知,
以上构建了基于领航跟随运动控制方法的控制器,并且证明了该控制器的稳定性。下面对该方法进行仿真与实验研究。
3 仿真分析与实验验证为验证系统及控制算法的正确性和有效性,利用仿真软件和硬件平台构建模拟/物理实验系统进行验证。仿真采取与期望轨迹重合(追踪)、与期望轨迹保持固定队形(编队)两种情况进行,便于在不同控制场景下对结果分析。
3.1 仿真分析仿真研究基于Gazebo机器人仿真软件构建的运动学与控制仿真平台。仿真固定参数以实际硬件平台为参考,其固定参数值如表1所示。
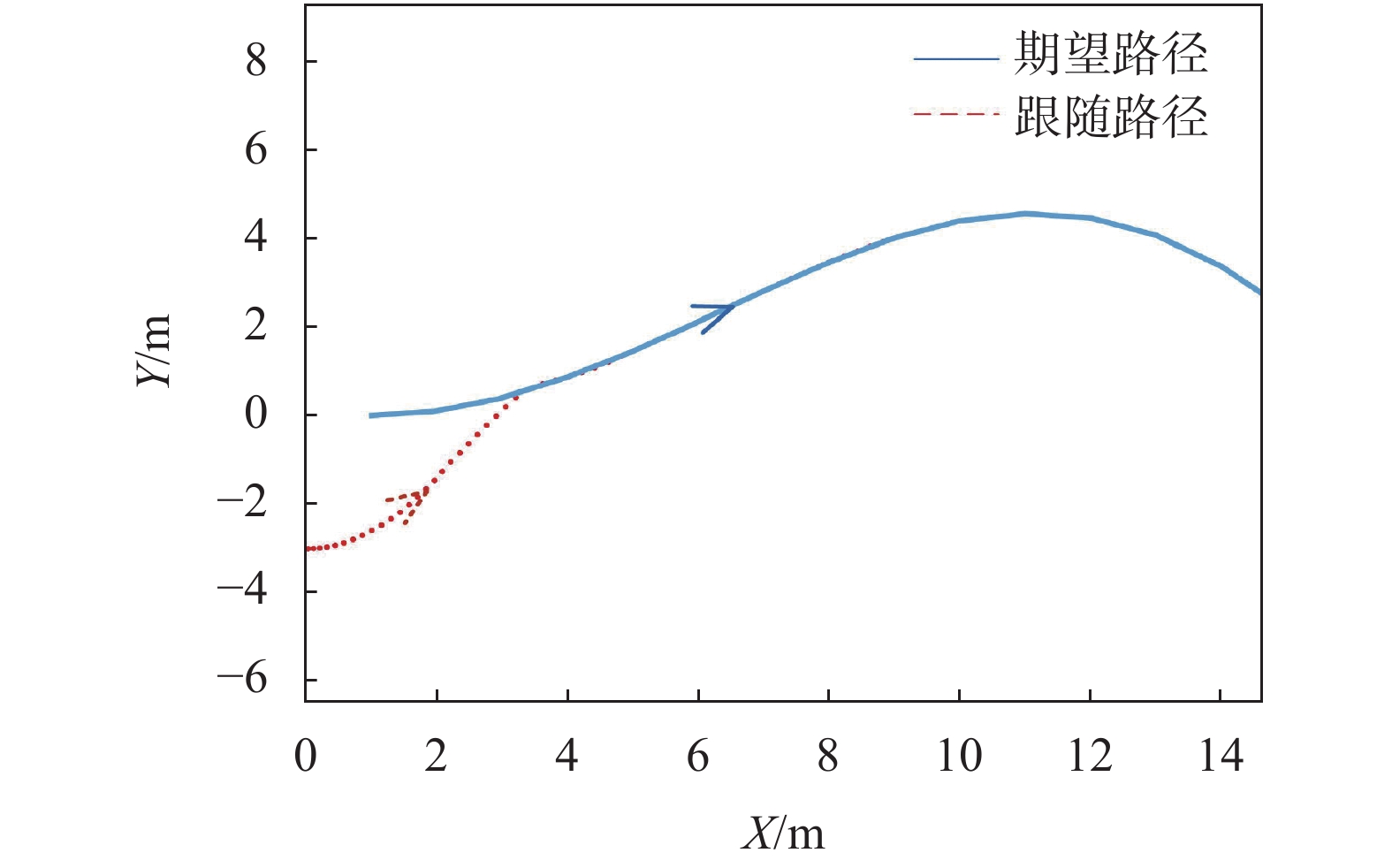
设定虚拟领航机器人与期望轨迹追踪,即
|
|
图 3
|
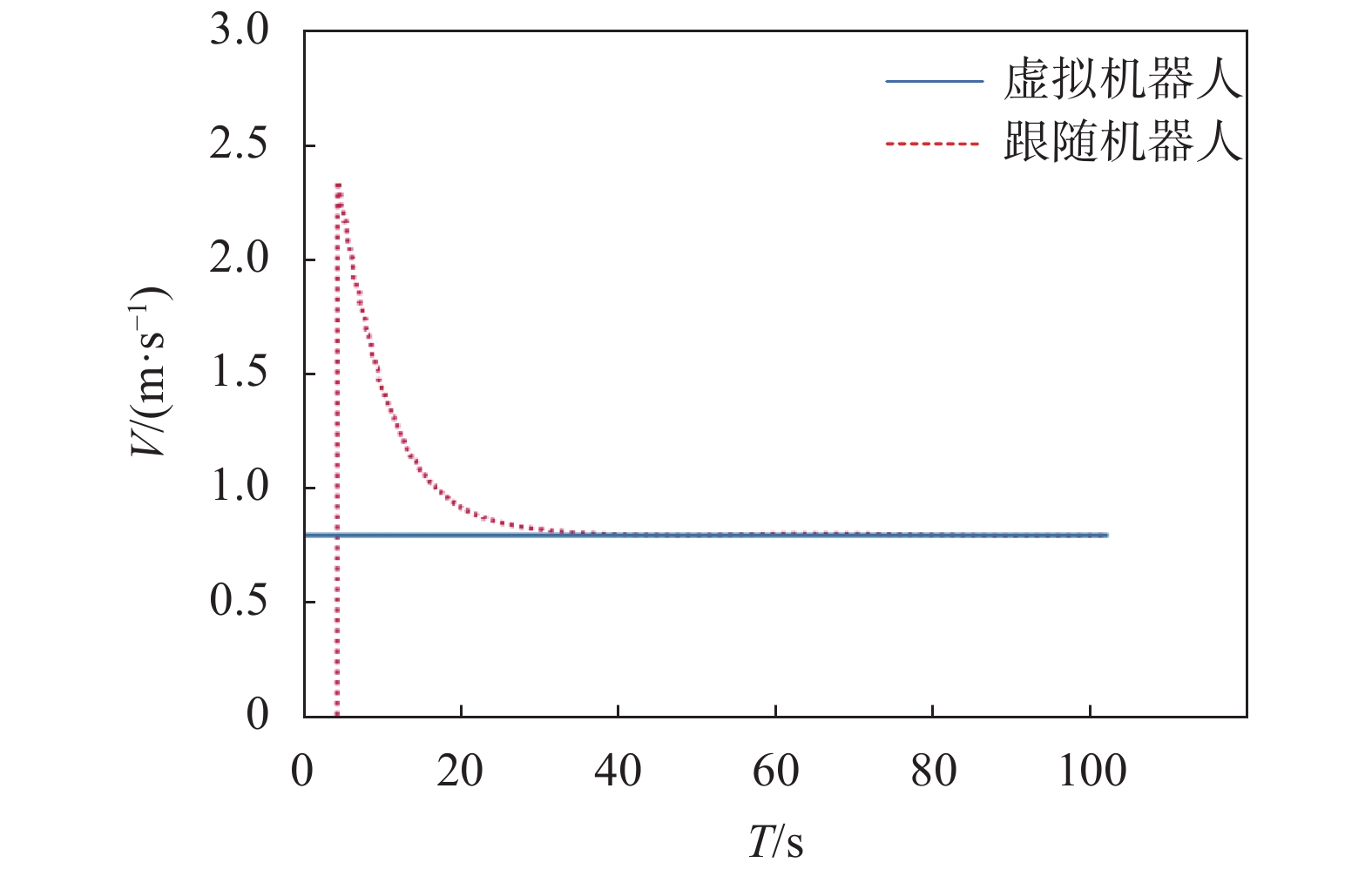
跟随机器人从任意初始位置开始运动,速度变化曲线如图4中虚线所示。由图可以看出,时间T从5 s左右速度开始变化,随后减小;从20 s左右开始,跟随机器人速度趋于稳定;30 s时,跟随机器人速度稳定在0.8 m/s。
|
|
图 4
|
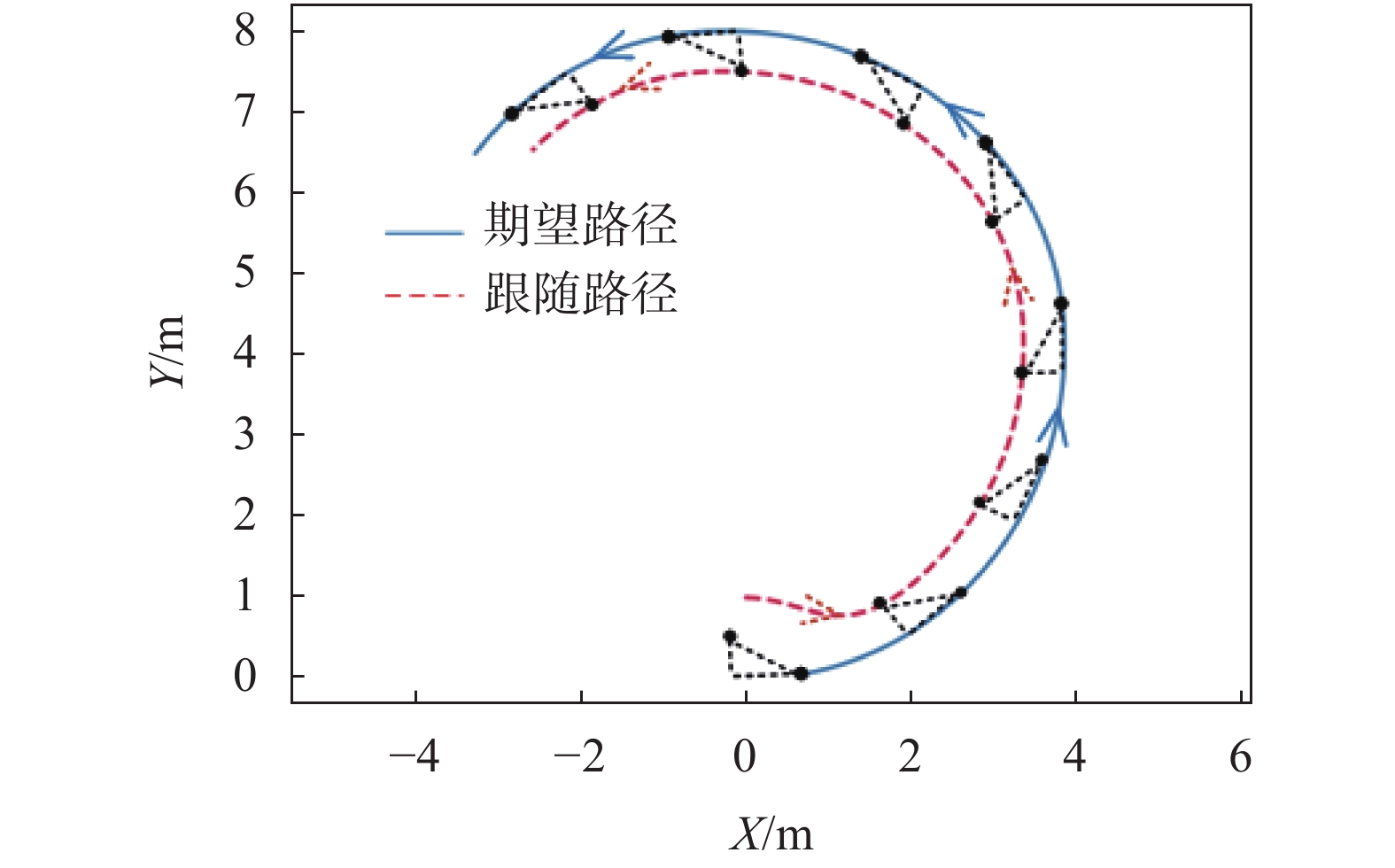
设定虚拟领航机器人与期望路径距离为0.5 m,与速度方向夹角为
|
|
图 5
|
跟随机器人速度变化曲线如图6中虚线所示。当时间T从25 s开始,跟随机器人速度趋于稳定;40 s时,跟随机器人速度稳定在0.8 m/s。
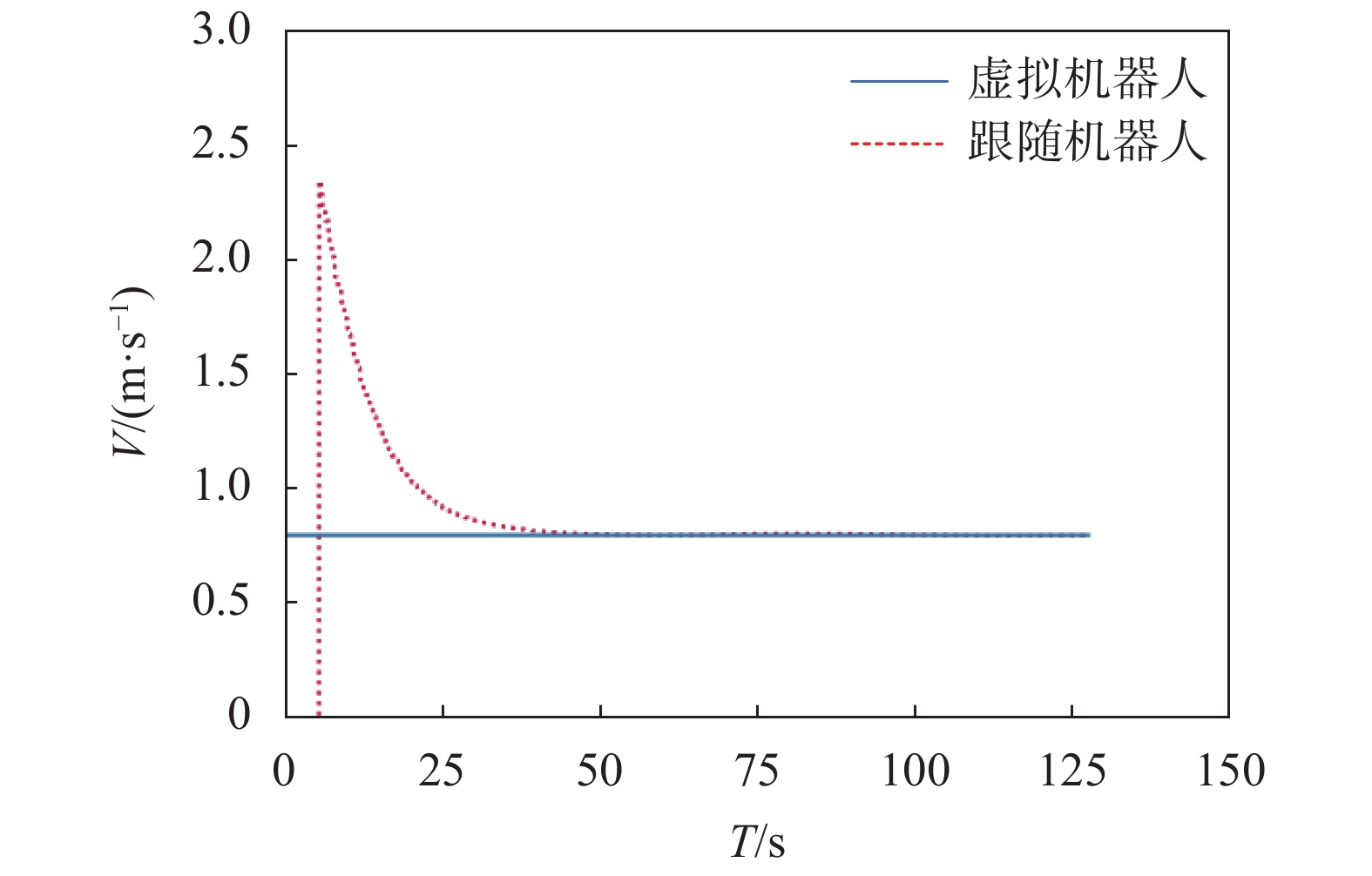
|
|
图 6
|
3.2 实验验证
为移动机器人控制构建物理实验系统。该实验系统的硬件部分主要由双轮差速驱动底盘、IMU模块、差分GPS定位模块(RTK)和主计算机(Raspberry Pi4B)组成。
主计算机主要通过传感器模块采集到的数据进行运动状态计算,并且通过输出控制指令完成对底盘的运动控制;底盘执行主计算机的控制指令,按照控制指令完成运动;IMU模块为九轴惯性测量模块,用于测量机器人的运动状态,包括加速度和航向角等;差分GPS定位模块实现机器人的实时定位功能,具体实现为:将差分GPS移动接收端安装于机器人的底盘上,通过接收卫星与基准站数据进行差分计算,从而提高机器人的定位精度。
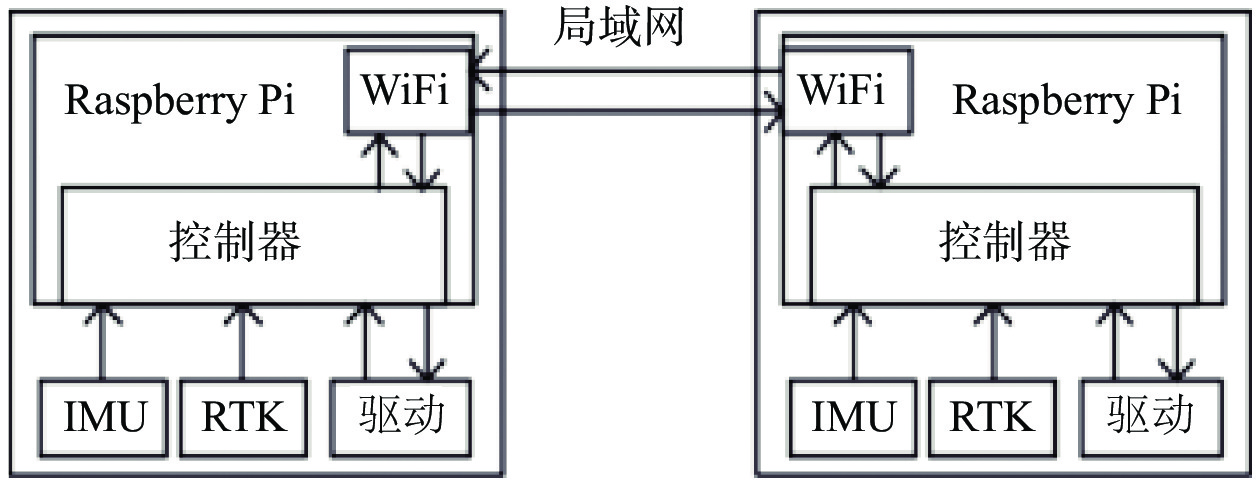
|
| 图 7 实验平台示意图 |

|
| 图 8 实验平台实物图 |
程序流程如图9所示。首先对跟随机器人进行状态初始化;然后根据GPS和IMU回传数据计算,并于期望位姿做姿态解算;通过结算结果,得到控制输入参数;最后输出给控制单元,并实时对跟随机器人状态进行监测,判断其是否达到预期位姿。
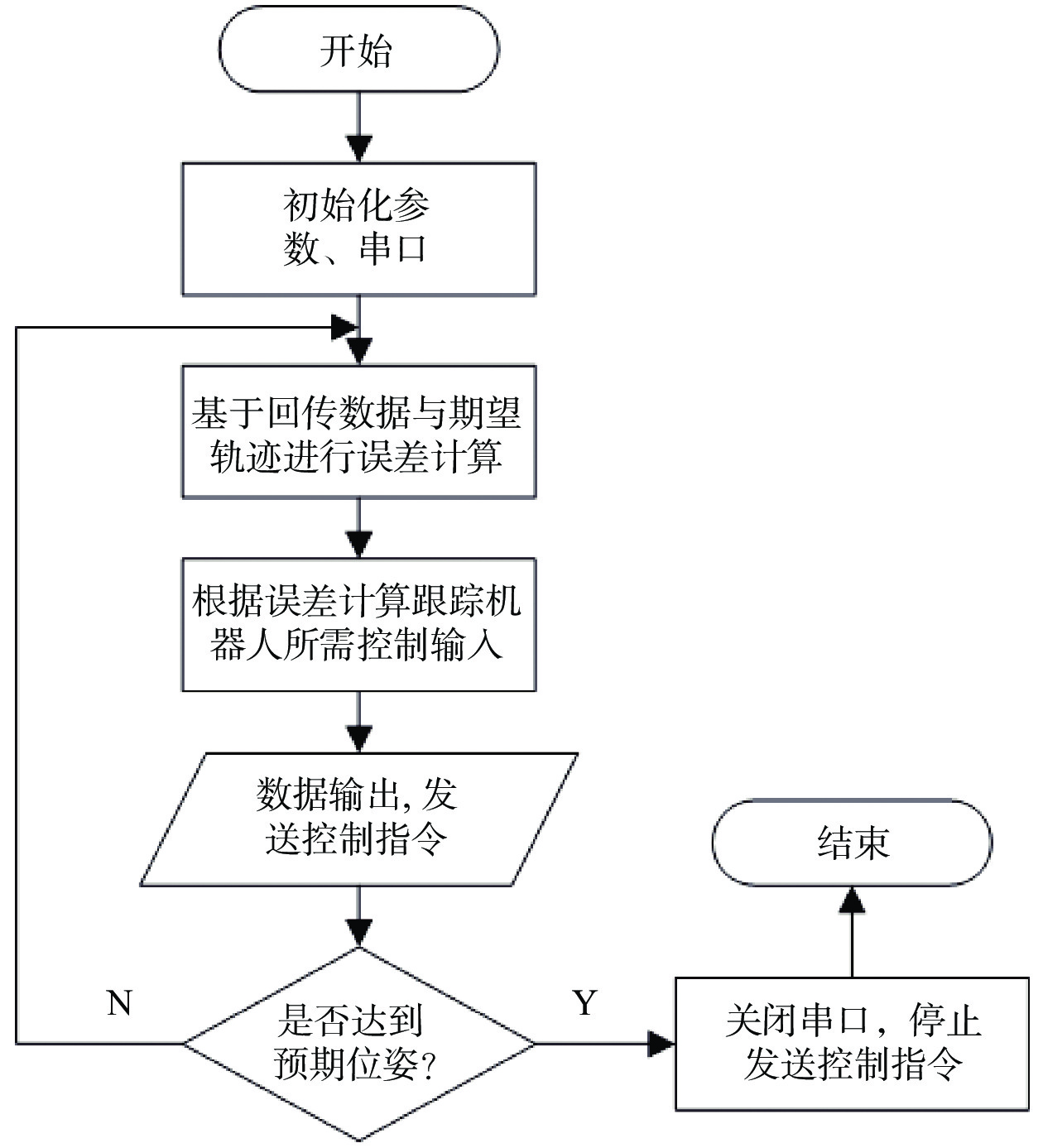
|
| 图 9 跟随机器人控制实验流程图 |
当
根据预设期望轨迹与虚拟领航机器人的当前位姿误差,计算跟随机器人所需控制输入参数,然后通过串口将运动控制指令发送给运动底盘。如此循环。
设定虚拟领航机器人与期望轨迹重合,即
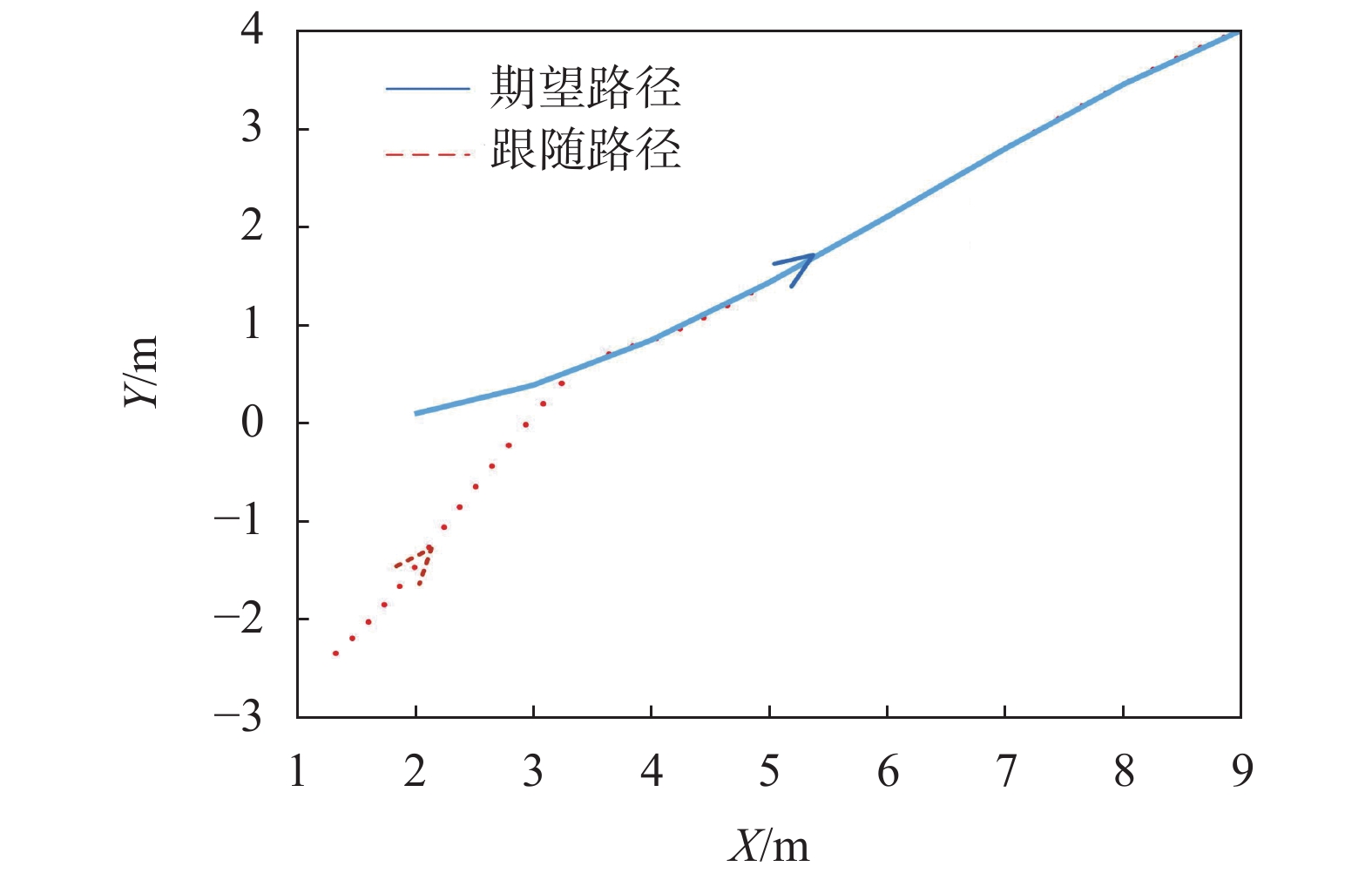
|
|
图 10
|
跟随机器人速度变化曲线如图11中虚线所示。当时间T从20 s开始,跟随机器人速度趋于稳定;35 s时,跟随机器人速度稳定在0.8 m/s。
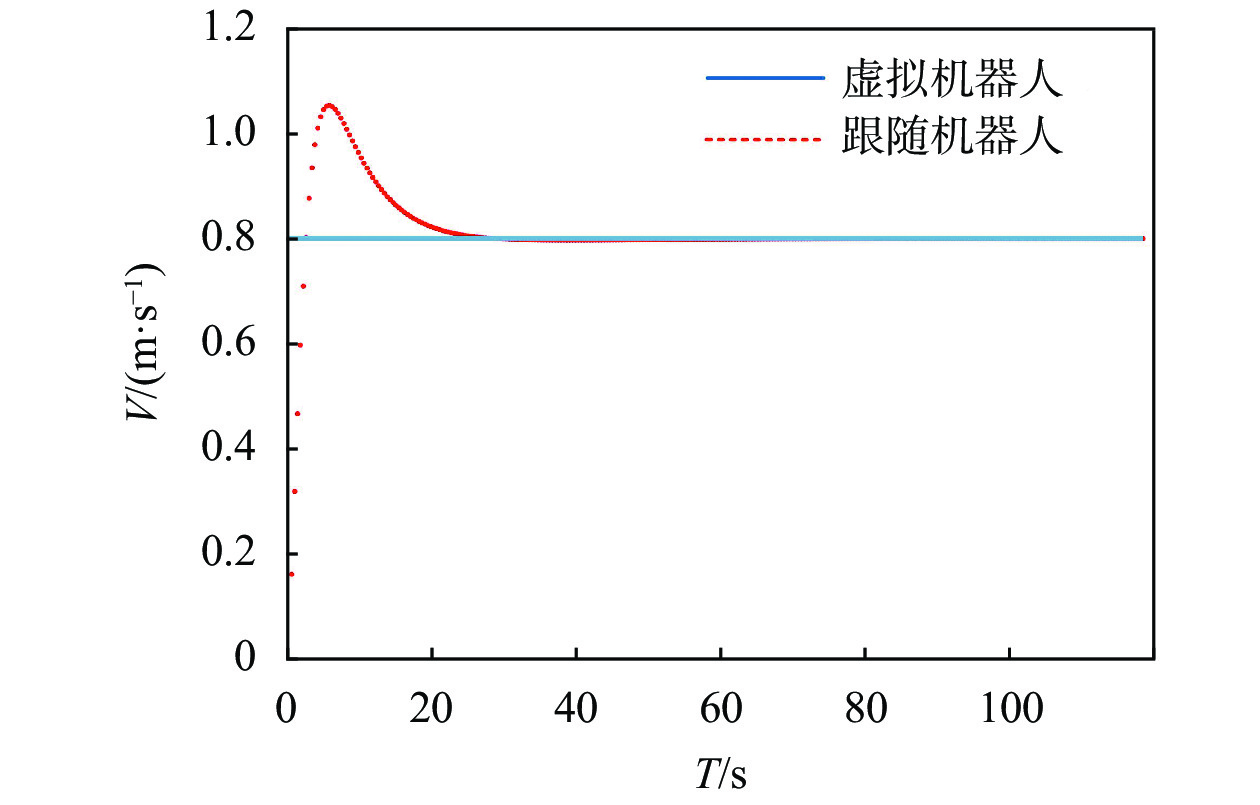
|
|
图 11
|
设定虚拟领航机器人与期望路径距离为0.5 m,与速度方向夹角为
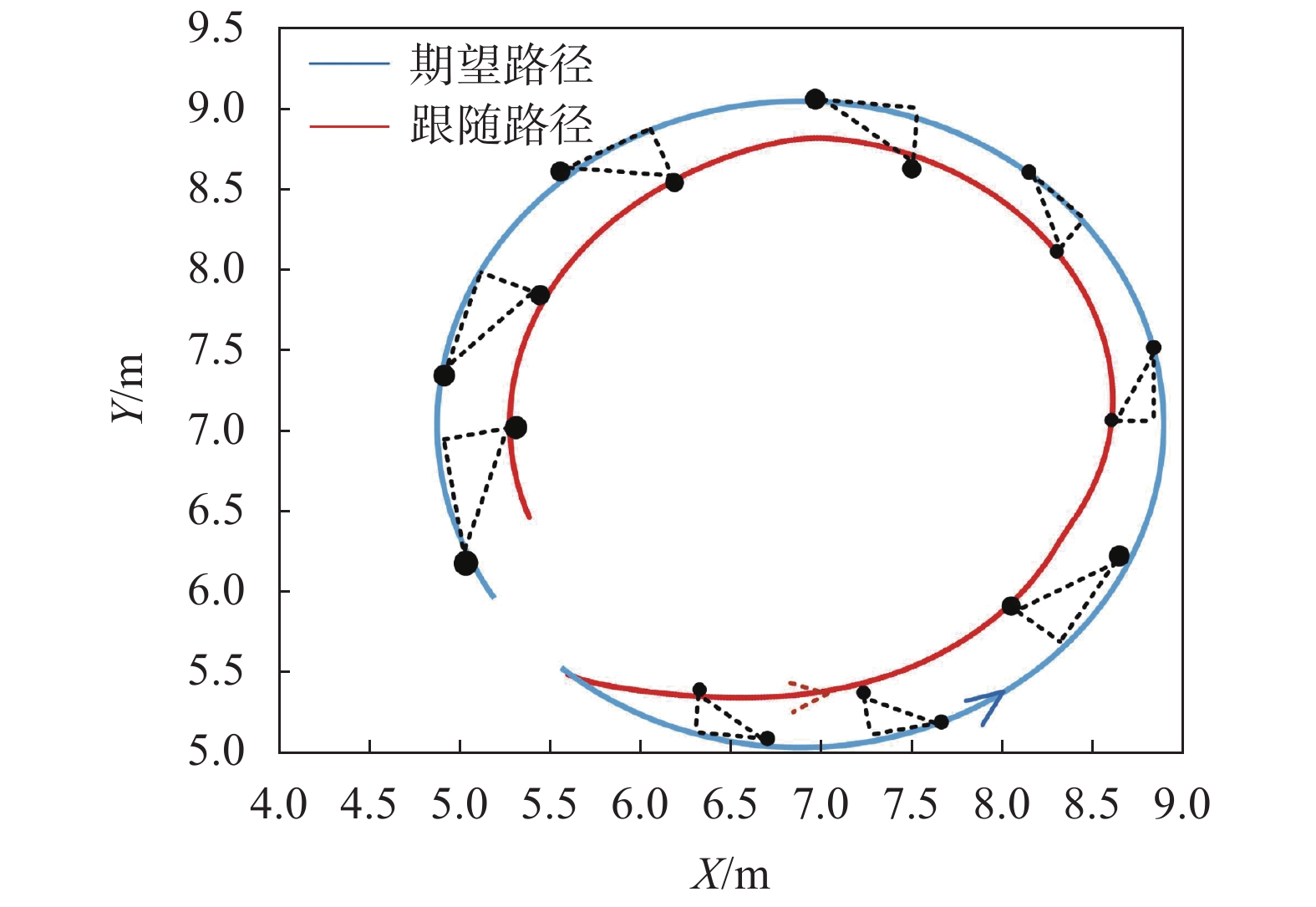
|
|
图 12
|
领航机器人以0.8 m/s速度运动时,跟随机器人变化曲线如图13虚线所示。当时间趋于50 s时,跟随机器人速度稳定在0.8 m/s。
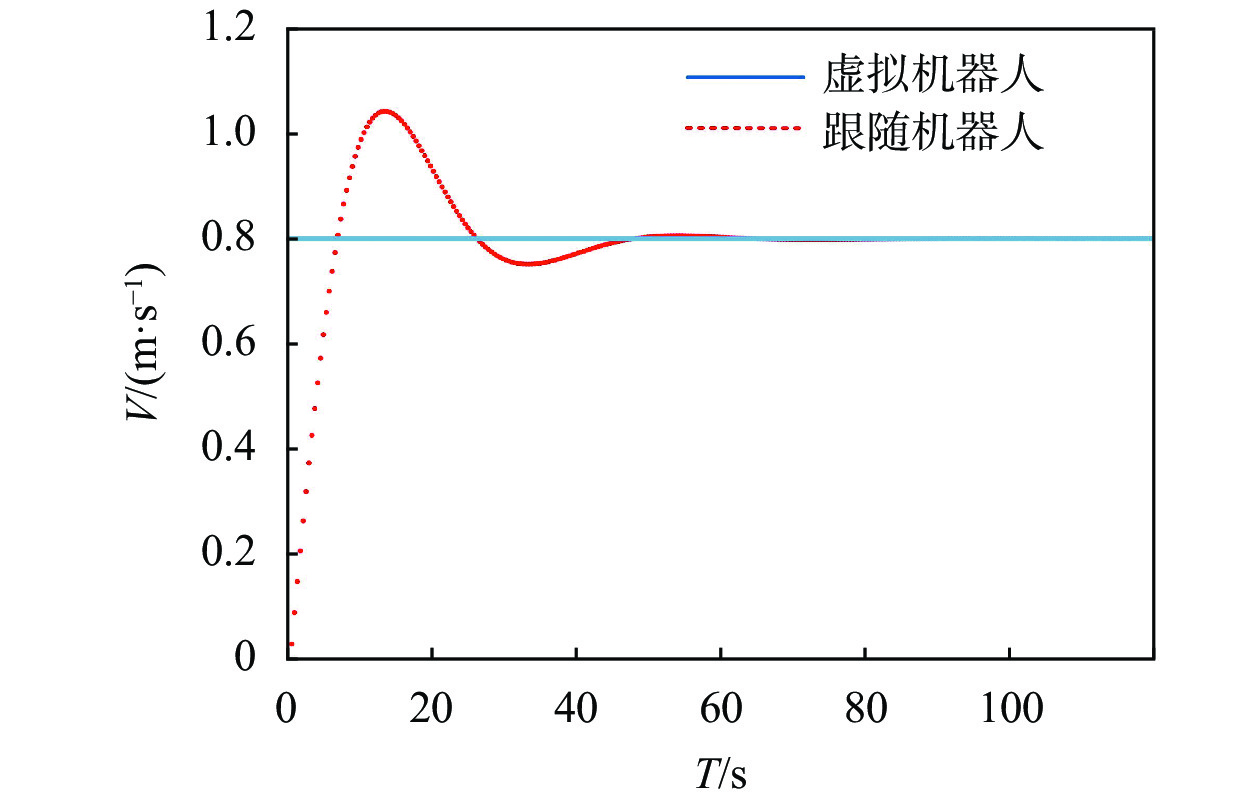
|
|
图 13
|
通过对比表2及前文中速度曲线可以看出,跟随机器人速度、位姿误差在仿真中收敛较快。并且,跟随期望轨迹比保持固定距离收敛耗时较少。
| 参数设定 | 仿真 | 实验 |
|
|
30 s | 40 s |
|
|
35 s | 50 s |
在一定时间内,跟随机器人运动速度逐渐收敛至预期,
本文以轮式差分驱动机器人为实验对象,其由两个独立驱动的后轮控制,完成姿态变化。在此基础上,通过对差分驱动机器人运动学模型分析,设计了控制器并生成相应控制算法。利用仿真和硬件实验平台,在两种不同运动情况下,完成对控制算法的验证。仿真和实验结果表明:位姿误差收敛及速度收敛均能满足一般跟随控制需求,验证了控制算法与控制器的有效性与稳定性。
此外,本文提出的控制策略易于实现,只需合理设置
| [1] |
闵海波, 刘源, 王仕成, 等. 多个体协调控制问题综述[J].
自动化学报, 2012, 38(10): 1557-1570.
|
| [2] |
LIU S, SUN D, ZHU C G. Coordinated motion planning for multiple mobile robots along designed paths with formation requirement[J].
IEEE/ASME Transactions on Mechatronics, 2011, 16(6): 1021-1031.
DOI:10.1109/TMECH.2010.2070843 |
| [3] |
余宏旺, 郑毓蕃. 多智能体系统在分布式采样控制下的动力学行为[J].
自动化学报, 2012, 38(3): 357-365.
|
| [4] |
DONG X, YU B, SHI Z, et al. Time-varying time-varying formation control for unmanned aerial vehicles: theories and applications[J].
IEEE Transactions on Control Systems Technology, 2015, 23(1): 340-348.
DOI:10.1109/TCST.2014.2314460 |
| [5] |
韩青, 孙树栋, 智睿瑞. 轨迹跟踪级联机器人编队控制方法[J].
控制与决策, 2016, 31(2): 317-323.
|
| [6] |
宋子浩, 吴斌, 周挺. 输入受限情况下的球形机器人轨迹跟踪控制[J].
中国测试, 2020, 46(5): 120-126.
DOI:10.11857/j.issn.1674-5124.2019120094 |
| [7] |
DESAI J P, OSTROWSKI J, KUMAR V. Controlling formations of multiple mobile robots[C]//Proceedings of IEEE International Conference on Robotics and Automation. Leuven: IEEE, 1998: 2864-2869.
|
| [8] |
LI X H, XIAO J Z, TAN J D. Modeling and controller design for multiple mobile robots formation control[C]//Proceedings of the 2004 IEEE International Conference on Robotics and Biomimetics, 2004: 838-843.
|
| [9] |
LI X, XIAO J, CAI Z. Backstepping based multiple mobile robots formation control[C]//Intelligent Robots and Systems, 2005. (IROS 2005). 2005 IEEE/RSJ International Conference on IEEE, 2005: 887-892.
|
| [10] |
DONG X W, ZHOU Y, REN Z, et al. Time-varying formation control for unmanned aerial vehicles with switching interaction topologies[J].
Control Engineering Practice, 2016, 46: 26-36.
DOI:10.1016/j.conengprac.2015.10.001 |
| [11] |
WANG R, DONG X W, LI Q D, et al. Distributed adaptive time-varying formation for multi-agent systems with general high-order linear time-invariant dynamics[J].
Journal of the Franklin Institute, 2016, 353(10): 2290-2304.
DOI:10.1016/j.jfranklin.2016.03.016 |
| [12] |
刘磊. 多移动机器人编队及协调控制研究[D]. 武汉: 华中科技大学, 2009.
|
| [13] |
RASEKHIPOUR Y, KHAJEPOUR A, CHEN S K, et al. A potential field-based model predictive path-planning controller for autonomous road vehicles[J].
IEEE Transactions on Intelligent Transportation Systems, 2017, 18(5): 1255-1267.
DOI:10.1109/TITS.2016.2604240 |
| [14] |
LEE G, CHWA D. Decentralized behavior-based formation control of multiple robots considering obstacle avoidance[J].
Intelligent Service Robotics, 2018, 11(1): 127-138.
DOI:10.1007/s11370-017-0240-y |
| [15] |
潘无为, 姜大鹏, 庞永杰, 等. 人工势场和虚拟结构相结合的多水下机器人编队控制[J].
兵工学报, 2017, 38(2): 326-334.
DOI:10.3969/j.issn.1000-1093.2017.02.017 |
| [16] |
DESAI J P, OSTROWSKI J P, KUMAR V. Controlling formations of multiple mobile robots[C]//Proceedings of IEEE International Conference on Robotics and Automation, 1998.
|
| [17] |
于涛, 王益博, 孙汉旭, 等. 基于干扰观测器的球形移动机器人直线运动控制[J].
中国测试, 2019, 45(9): 123-129.
DOI:10.11857/j.issn.1674-5124.2018100021 |
| [18] |
HAN T, GUAN Z H, CHI M, et al. Multi-formation control of nonlinear leader-following multiagent systems[J].
ISA Transactions, 2017, 69: 140-147.
DOI:10.1016/j.isatra.2017.05.003 |
| [19] |
黄烨笙, 徐郑攀, 陈远明等. 无人艇自主靠泊控制系统设计[J].
中国测试, 2020, 46(10): 111-117.
DOI:10.11857/j.issn.1674-5124.2020050071 |
| [20] |
易国, 毛建旭, 王耀南, 等. 非完整移动机器人领航-跟随编队分布式控制[J].
仪器仪表学报, 2017, 38(9): 2266-2272.
DOI:10.3969/j.issn.0254-3087.2017.09.022 |
 2021, Vol. 47
2021, Vol. 47



 ,
,