文章信息
- 徐新光, 郭亮, 王者龙, 杜艳, 李琮琮
- XU Xinguang, GUO Liang, WANG Zhelong, DU Yan, LI Congcong
- 功率反馈非仿射励磁系统扩展反演自适应L2增益控制
- Extend back-stepping adaptive L2-gain control of non-affine excitation system with power feedback
- 中国测试, 2019, 45(3): 151-156
- CHINA MEASUREMENT & TEST, 2019, 45(3): 151-156
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018020020
-
文章历史
- 收稿日期: 2018-02-07
- 收到修改稿日期: 2018-04-12
2. 国网山东省电力公司,山东 济南 250002
2. State Grid Shandong Electric Power Company, Jinan 250002, China
励磁系统作为电力系统重要组成部分,对于提高电力系统暂态稳定和抑制低频振荡具有重要意义[1~2]。由于励磁系统具有较强的非线性特征,所以传统的依据励磁系统定点线性化模型的控制方法对于保证电力系统大范围稳定运行的能力有限[3]。因此,为了更好地提高励磁控制的性能,保证电力系统的大范围稳定运行,许多学者在励磁系统非线性控制方面进行着不懈的努力,并取得了许多显著的成果。
文献[4]采用基于微分几何反馈线性化方法,将非线性系统分解为线性与非线性两部分,线性部分采用最优二次型方法设计控制律,非线性部分采用动态扩张的方法,最终实现整体线性化,并得到了最优控制解。文献[5]基于协同控制理论,通过选取端电压、功率、转速偏差构建流形,并合理设计控制律,使得系统沿此流形稳定于平衡点,但是控制律中含有交、直轴电流微分项,增加了测量难度。文献[6-7]设计不同类型滑模面相应的控制律,但是用以实现励磁系统不确定性估计的观测器实现比较复杂。文献[8-9]充分采用反演设计方法抵消励磁系统的非线性部分,但是并未对系统的外部干扰影响进行分析。文献[10]基于H∞理论,通过求解线性矩阵不等式,保证干扰对期望输出的影响小于给定值;文献[11-12]基于微分几何原理,通过微分同胚变换,将励磁系统等效为线性系统,经过对干扰或模型不确定性的状态观测或预测,最终采用变结构或线性系统最优控制方法得到了励磁控制解,但是控制律中含有转速微分项,并且状态观测或预测算法中有较多参数需要调整。文献[13]基于伪广义Hamilton理论对广域多机系统中存在的时滞控制问题进行了分析。文献[14]通过设计布鲁诺夫斯基标准型简化了非线性励磁控制难度,但是没有考虑干扰抑制问题。文献[15-16]采用非线性鲁棒控制的方法对励磁系统的干扰抑制和参数自适应控制进行了分析,但是由于受状态变量和励磁系统模型选取限制,控制律的设计过程比较复杂。
本文在励磁系统模型分析中,将电磁功率
当受到大扰动影响或在大范围动态工作过程中,考虑到电抗饱和、惯性时间常数误差、阻尼系数变化等不确定性以及外部电磁、力矩等扰动影响[15],励磁系统模型可表示为[17]
| ${{\dot \delta }} = {{\omega }} - {{{\omega }}_{\rm{N}}}$ | (1) |
| ${{\dot \omega }} = \frac{{{{{\omega }}_{\rm{N}}}}}{{{M}}}{{{P}}_{\rm{m}}} - \frac{{{D}}}{{{M}}}({{\omega }} - {{{\omega }}_{\rm{N}}}) - \frac{{{{{\omega }}_{\rm{N}}}}}{{{M}}}{{{P}}_{\rm{e}}} + {{{d}}_1}$ | (2) |
| ${\dot E'_{\rm{q}}} = - \frac{1}{{{T'_{\rm{d}}}}}E_{\rm{q}}' + \frac{1}{{{T_{{\rm{d}}0}}}}\frac{{{x_{\rm{d}}} - {x'_{\rm{d}}}}}{{{x'_{\rm{d}}}}}U\cos {{\delta }} + \frac{1}{{{T_{{\rm{d}}0}}}}{E_{\rm{f}}} + {d_{{2}}}$ | (3) |
式中:
假定励磁系统稳定工作点为
| ${{{\dot x}}_1} = {{{x}}_2}$ | (4) |
| ${{{\dot x}}_2} = {{{a}}_1}\Delta {{{P}}_{\rm{e}}} - {{\theta }}{{{x}}_2} + {{{d}}_1}$ | (5) |
| ${{{\dot x}}_3} = {{v}} + {{{d}}_2}$ | (6) |
| ${{y}} = {\left[ {{{{q}}_1}{{{x}}_1} \;\; {{{q}}_2}{{{x}}_2} \;\; {{{q}}_3}{{{x}}_3}} \right]^{\rm{T}}}$ | (7) |
其中,
由于模型式(4)~式(7)不具备严参数反馈结构特征,所以不能直接采用常规反演自适应L2增益控制方法实现励磁系统的L2增益稳定控制。为此,本文提出一种扩展反演自适应L2增益励磁控制方法。
2 扩展反演自适应L2增益励磁控制实现取
| ${\dot V_1} = {e_1}{\dot e_1} = {e_1}{x_2}$ | (8) |
由Lyapunov稳定理论和反演设计理论可知,可将
| $x_2^* = - {m_1}{e_1}$ | (9) |
其中:
常规反演设计中,
取
| ${H_1} = {e_1}( - {m_1}{e_1} + {e_2}) + {e_2}{\dot e_2}\frac{1}{2}\left(\sum\limits_{j = 1}^3 {q_j^2x_j^2} - {\gamma ^2}d_1^2\right)$ | (10) |
| ${\dot e_2} = {{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \theta }}{{{x}}_2} + {{{d}}_1} + {m_1}{x_2}$ | (11) |
由式(10)、式(11)得
| $\begin{split} {H_1} = & - {m_1}e_1^2 + \displaystyle\frac{1}{2}\left(\displaystyle\sum\limits_{j = 1}^3 {q_j^2x_j^2} - {\gamma ^2}d_1^2\right) + \\ &{e_2}({e_1}{{ + }}{{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \theta }}{{{x}}_2} + {{{d}}_1} + {m_1}{x_2}) \\ \end{split} $ | (12) |
由式(12)得
| $\begin{split} {H_1} =& - {\left(\displaystyle\frac{{{e_2}}}{\gamma } - \displaystyle\frac{{\gamma {d_1}}}{2}\right)^2} + \displaystyle\frac{{e_2^2}}{{{\gamma ^2}}} - {m_1}e_1^2 - {{ }}\displaystyle\frac{{{\gamma ^2}d_1^2}}{4} + \\ &\displaystyle\frac{1}{2}\displaystyle\sum\limits_{j = 1}^3 {q_j^2x_j^2} + {{ }}{e_2}({e_1}{{ + }}{{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \theta }}{{{x}}_2} + {m_1}{x_2}) \leqslant \\ & - {m_1}e_1^2 + \displaystyle\frac{{e_2^2}}{{{\gamma ^2}}} - \displaystyle\frac{{{\gamma ^2}d_1^2}}{4} + \displaystyle\frac{1}{2}\displaystyle\sum\limits_{j = 1}^3 {q_j^2x_j^2} + \\ & {e_2}({e_1}{{ + }}{{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \theta }}{{{x}}_2} + {m_1}{x_2}) \end{split} $ | (13) |
取虚拟控制量
| $x_3^* = - {m_2}{e_2}$ | (14) |
其中:
则可得误差变量
取
| $\begin{split} {H_2} =& {H_1} - \frac{{{\gamma ^2}d_2^2}}{2} + K{{\dot e}_3} - \frac{{\tilde \theta {\dot {\hat \theta}} }}{\rho } \leqslant \\ & - {m_1}e_1^2 + \frac{{e_2^2}}{{{\gamma ^2}}} - \frac{{{\gamma ^2}d_1^2}}{4} + \frac{1}{2}\sum\limits_{j = 1}^3 {q_j^2x_j^2} - \\ &\frac{{{\gamma ^2}d_2^2}}{2} - \frac{{\tilde \theta {\dot {\hat \theta}} }}{\rho } + K({{v}} + {{{d}}_2} - \dot x_3^*) + \\ &{e_2}({e_1}{{ + }}{{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \theta }}{{{x}}_2} + {m_1}{x_2}) \\ \end{split} $ | (15) |
| $\dot x_3^* = {e_2}({{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \theta }}{{{x}}_2} + {{{d}}_1} + {m_1}{x_2})$ | (16) |
其中:
由式(15)得
| $\begin{split} {H_2} \leqslant & - {m_1}e_1^2 - {\left(\frac{{\gamma {d_1}}}{2} - \frac{{K{m_2}}}{\gamma }\right)^2} - {\left(\frac{{\gamma {d_2}}}{{\sqrt 2 }} - \frac{{\sqrt 2 K}}{{2\gamma }}\right)^2} - \\ &\frac{{\tilde \theta {\dot {\hat \theta}} }}{\rho } + \frac{{{K^2}(1 + 2m_2^2)}}{{2{\gamma ^2}}} + \frac{{e_2^2}}{{{\gamma ^2}}} + \frac{1}{2}\sum\limits_{j = 1}^3 {q_j^2x_j^2} + \\ &({{K}}{{{m}}_2} + {e_2})({{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \theta }}{{{x}}_2} + {m_1}{x_2}) + K{{v}} + {e_1}{e_2} \end{split} $ | (17) |
由式(17)可得控制律和参数自适应律为
| $\begin{split} v =& - {K^{ - 1}}\Bigg[({{K}}{{{m}}_2} + {e_2})({{{a}}_1}\Delta {{{P}}_{\rm{e}}}{{ - \hat \theta }}{{{x}}_2} + {m_1}{x_2}) + \\ &{e_1}{e_2} + \frac{{{K^2}(1 + 2m_2^2)}}{{2{\gamma ^2}}} + \frac{{e_2^2}}{{{\gamma ^2}}} + \frac{1}{2}\sum\limits_{j = 1}^3 {q_j^2x_j^2} \Bigg] \end{split} $ | (18) |
| $\dot {\hat \theta} = {{ - }}\rho ({{K}}{{{m}}_2} + {e_2}){{{x}}_2}$ | (19) |
将式(18)、式(19)代入式(17)得
| ${H_2} \leqslant - {m_1}e_1^2 - {\left(\frac{{\gamma {d_1}}}{2} - \frac{{K{m_2}}}{\gamma }\right)^2} - {\left(\frac{{\gamma {d_2}}}{{\sqrt 2 }} - \frac{{\sqrt 2 K}}{{2\gamma }}\right)^2}$ | (20) |
由式(20)得
| ${\dot V_3} + \frac{1}{2}(\left\| {y} \right\| - {\gamma ^2}\left\| {\varepsilon } \right\|) \leqslant 0$ | (21) |
式(21)积分可得耗散不等式:
| ${\int_0^{{T}} {\left\| {{y}} \right\|} ^2}{\rm d}t \leqslant {\gamma ^2}{\int_0^{{T}} {\left\| {\varepsilon } \right\|} ^2}{\rm d}t + 2{V_3}({x_0})$ | (22) |
由式(22)可知,采用控制律式(18)和参数自适应律式(19),可以实现L2增益控制。
由式(18)、式(19)可知励磁控制输入是关于
| $\left[ \begin{array}{l} {i_{{}_{\rm{D}}}}\\ {i_{{}_{\rm{Q}}}} \end{array} \right] = \sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}{c}} 1 & { - 1/2} & { - 1/2}\\ 0 & { - \sqrt 3 /2} & {\sqrt 3 /2}\\ {1/\sqrt 2 } & {1/\sqrt 2 } & {1/\sqrt 2 } \end{array}} \right]\left[ \begin{array}{l} {i_{\rm{a}}}\\ {i_{\rm{b}}}\\ {i_{\rm{c}}} \end{array} \right]$ | (23) |
| $\left[ \begin{array}{l} {u_{{}_{\rm{D}}}}\\ {u_{{}_{\rm{Q}}}} \end{array} \right] = \sqrt {\frac{2}{3}} \left[ {\begin{array}{*{20}{c}} 1 & { - 1/2} & { - 1/2}\\ 0 & { - \sqrt 3 /2} & {\sqrt 3 /2}\\ {1/\sqrt 2 } & {1/\sqrt 2 } & {1/\sqrt 2 } \end{array}} \right]\left[ \begin{array}{l} {u_{\rm{a}}}\\ {u_{\rm{b}}}\\ {u_{\rm{c}}} \end{array} \right]$ | (24) |
| ${P_{\rm{e}}} = {u_{{}_{\rm{D}}} }{i_{{}_{\rm D}}} + {u_{{}_{\rm Q}}}{i_{{}_{\rm{Q}}} }$ | (25) |
| ${Q_{\rm{e}}} = {u_{{}_{\rm Q}}}{i_{{}_{\rm D}}} - {u_{{}_{\rm D}}}{i_{{}_{\rm{Q}}} }$ | (26) |
| $U = \sqrt {u_{\rm{D}} ^2 + u_{\rm{Q}} ^2} $ | (27) |
通过采集发电机的端电压、转速变化量、功角变化量、有功变化量、有功功率和无功功率,代入控制律式(18)和参数自适应律式(19)可以得到扩展反演自适应L2增益励磁控制输出,进而控制励磁系统受到扰动后依然保持稳定运行。
3 仿真验证与结论分析为验证所提扩展反演自适应L2增益控制方法有效性,并与传统PI控制进行对比分析,进行如下仿真试验。仿真中励磁系统模型参数如表1所示。
|
|
|
|
|
| 1.3 | 0.3 | 4.4 | 1.51 |
| M/s |
|
|
|
| 3.2 | 1.03 | 0.26 | 1.0 |
3.1 负载增加时的仿真
在0.6 s时发电机突然增加50%负载,并在0.7 s时恢复原有负载,常规PI控制仿真图如图1所示。采用扩展反演自适应L2增益控制时,仿真参数为:
|
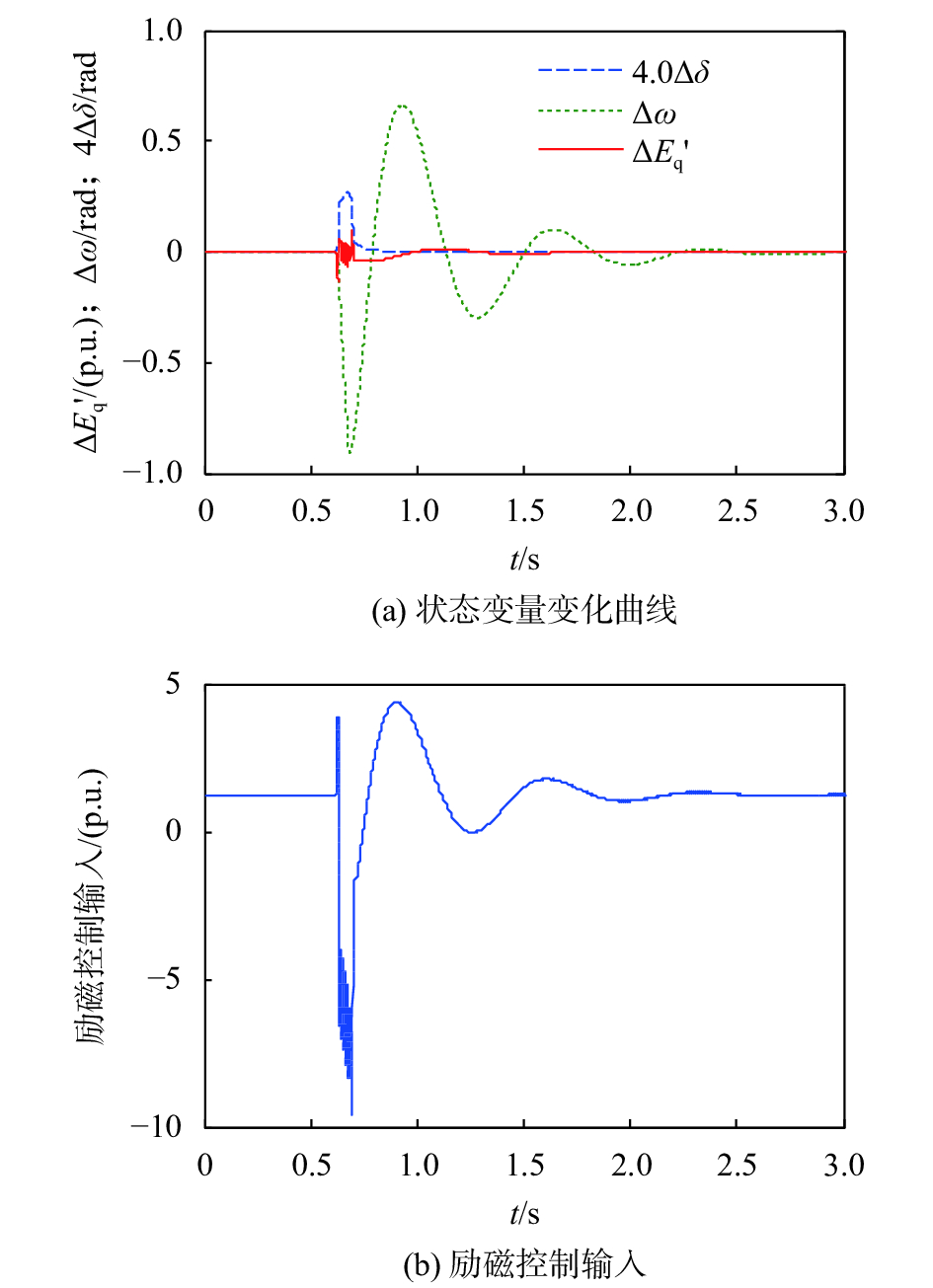
| 图 1 负载突增时PI控制仿真 |
|
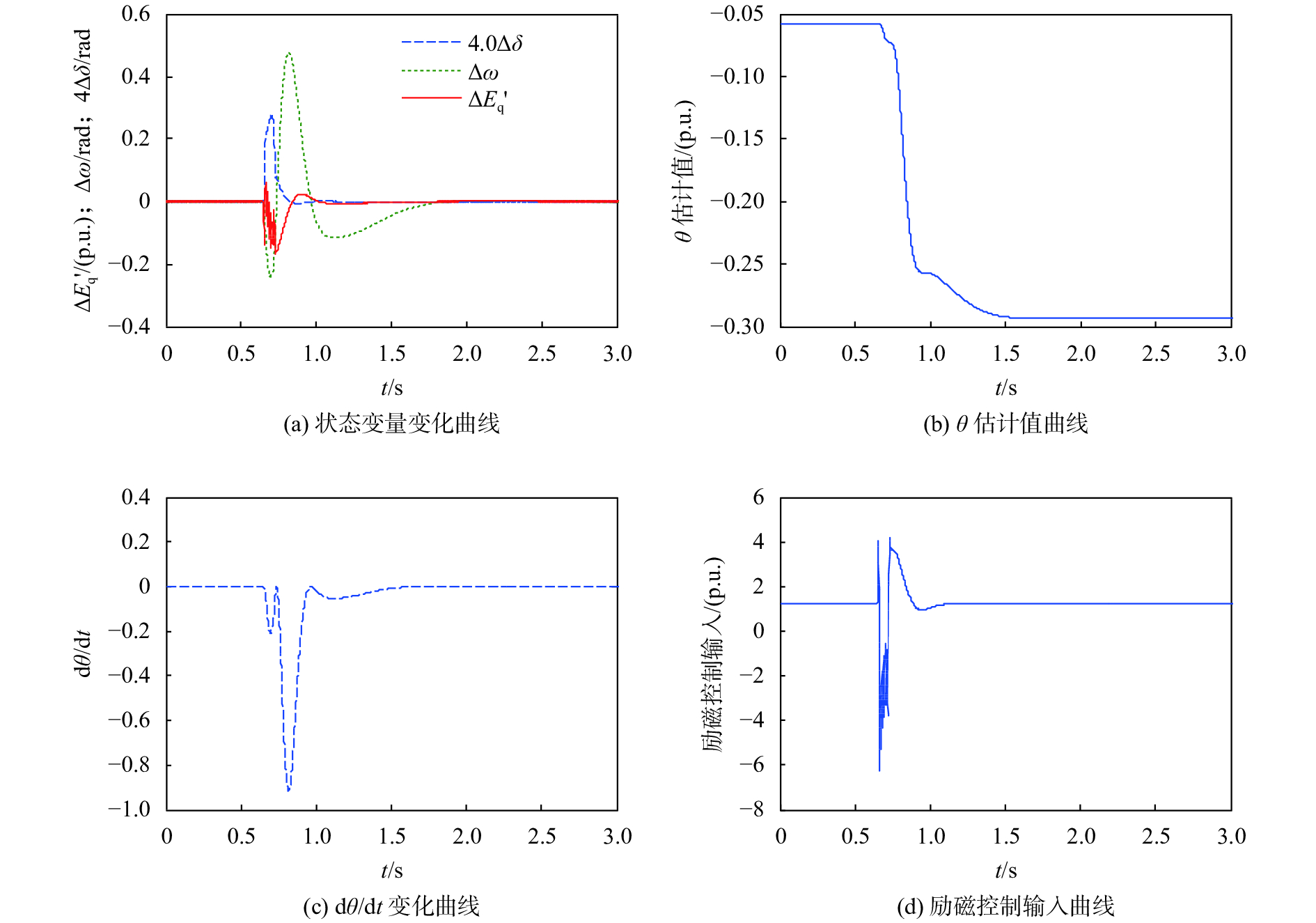
| 图 2 负载突增时扩展反演自适应L2增益控制仿真 |
比较图1、图2可知:当在0.6 s出现负载扰动后,相对于传统的常规PI控制,采用本文所提的扩展反演自适应L2增益控制时,状态变量的恢复时间由原来的大约1.7 s减小至大约1.0 s,转速和暂态电势波动时的最低值明显增加,有利于频率和电压的快速恢复,不确定参数的估计速度较快,在0.5 s内基本完成估计跟随,具有很好的跟随特性,能够满足励磁控制需要。
3.2 三相短路故障大扰动时的仿真在1.1 s时在并网变压器二次侧发生三相短路故障,并在1.2 s时切除三相短路故障。采用常规PI控制方式仿真图形如图3所示,采用扩展反演自适应L2增益控制仿真图形如图4所示。扩展反演自适应L2增益控制采用的控制参数同3.1节。
|
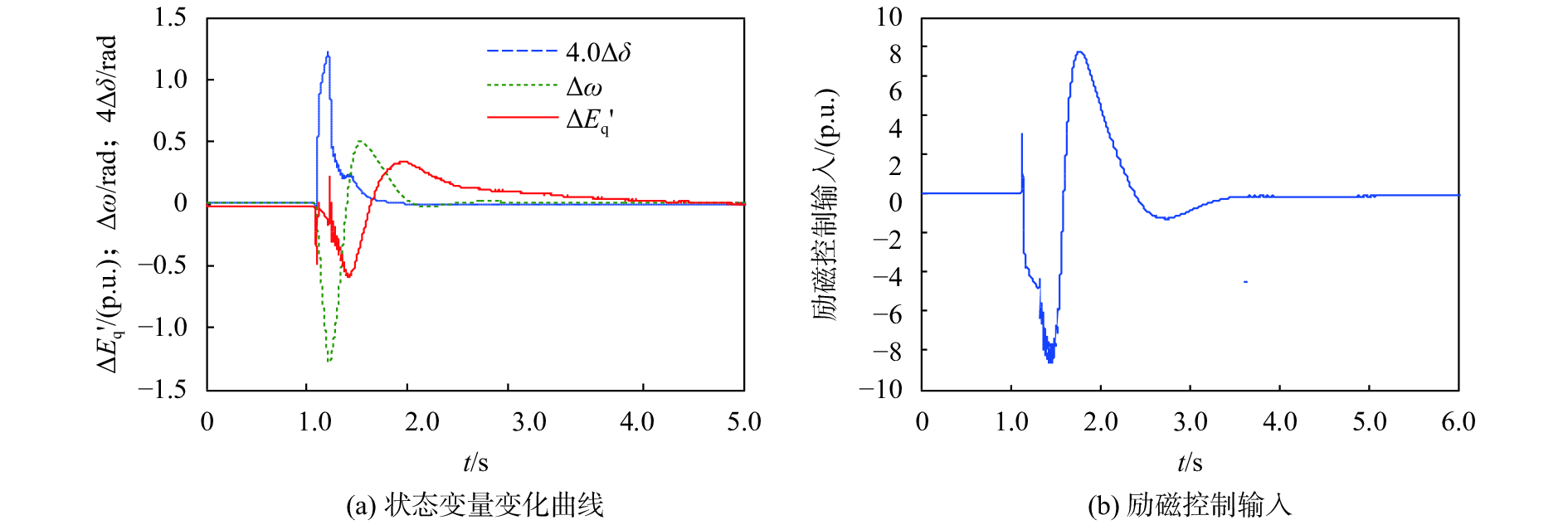
| 图 3 三相短路故障时PI控制仿真 |
|
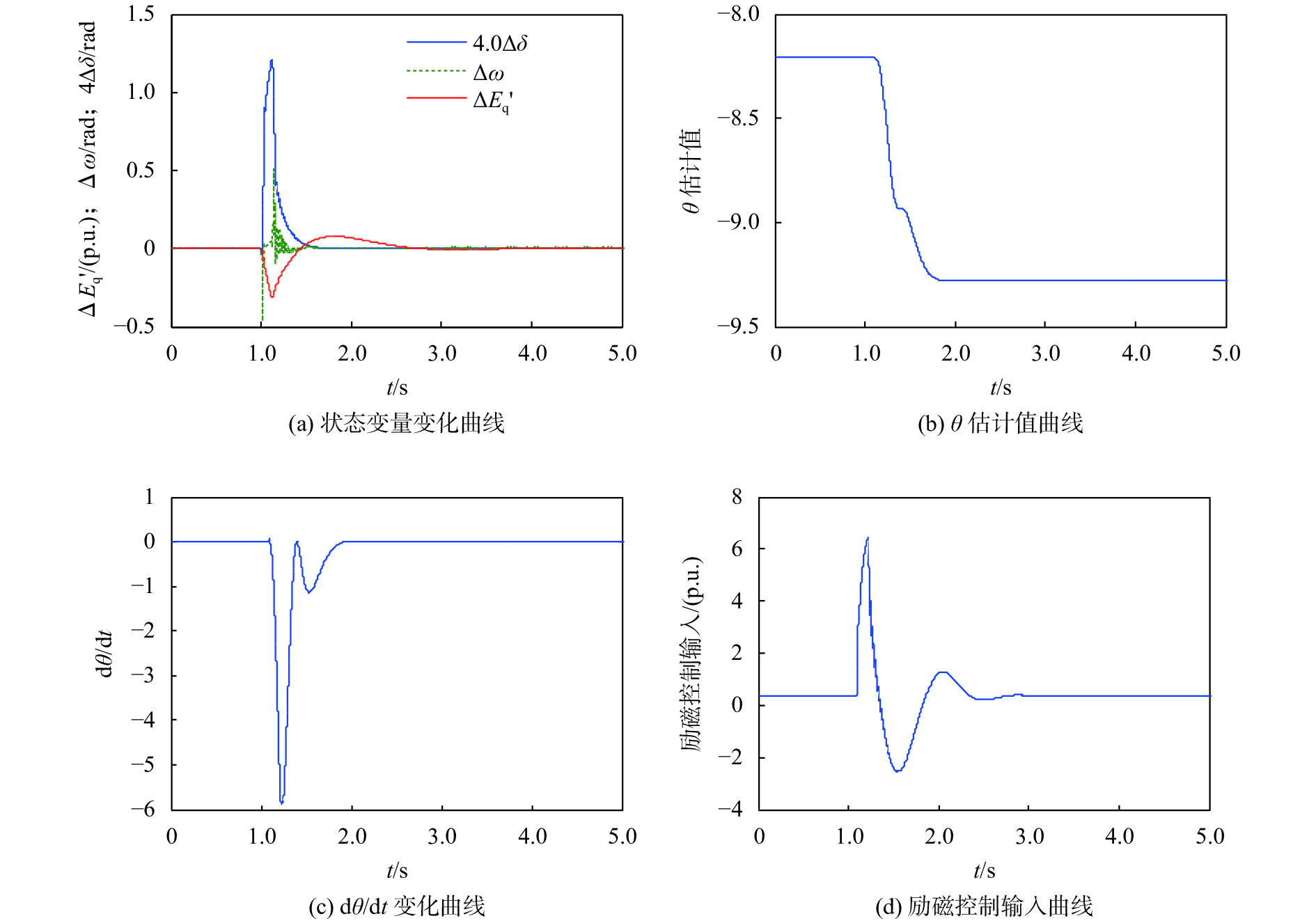
| 图 4 三相短路故障时扩展反演自适应L2增益控制仿真 |
比较图3、图4可知:当发生短时三相短路故障大扰动时,采用本文所提的扩展反演自适应L2增益控制可使发电机更能够快速恢复稳定运行,相对于传统的常规PI控制,暂态电势的的恢复稳定时间由2.5 s缩短为1.5 s,超调量明显降低,且励磁控制的幅值明显降低,不确定参数的估计速度较快,在0.8 s内完成估计跟随,具有很好的跟随特性,能够满足励磁控制需要。
4 结束语本文通过选取电磁功率作为整体测量量,简化了励磁系统模型,鉴于等效后的模型不具备严参数反馈结构,提出一种扩展反演自适应L2增益励磁控制新方法,其控制律中涉及的状态变量为端电压、转速、功率等可以直接测量得到的物理量,因此该方法可以较方便地应用于工程实际中。通过开展负载扰动和三相接地故障仿真测试实验,进一步证明了所提方法的正确性。仿真结果说明该方法对于提高系统的稳定速度、降低电压冲击具有明显的效果,为提高电力系统暂态稳定能力提供了一种新的励磁控制途径。
| [1] |
BO Z Q, LIN X N, WANG Q P, et al. Developments of power system protection and control[J].
Protection and Control of Modern Power Systems, 2016(1): 1-7.
DOI:10.1186/s41601-016-0016-y |
| [2] |
张静, 李志强, 何凤军, 等. 全过程励磁控制对电力系统暂态稳定性的影响[J].
电力系统自动化, 2014, 38(15): 124-129.
DOI:10.7500/AEPS20131017002 |
| [3] |
卢强, 梅生伟, 孙元章. 电力系统非线性控制[M]. 北京: 清华大学出版社, 2008.
|
| [4] |
李啸骢, 郑涛, 梁志坚, 等. 水轮机水门、励磁与电气制动系统非线性综合控制[J].
电力自动化设备, 2016, 36(7): 97-103.
|
| [5] |
赵平, 姚伟, 王少荣, 等. 采用协同控制理论的同步发电机非线性励磁控制[J].
电力系统保护与控制, 2013, 41(23): 1-7.
DOI:10.7667/j.issn.1674-3415.2013.23.001 |
| [6] |
赵辉, 王亚菲, 王红君, 等. 基于滑模变结构控制的余热发电机机组励磁控制研究[J].
电力系统保护与控制, 2015, 43(6): 8-13.
|
| [7] |
张虹, 于雷, 徐滨. 基于改进PSO的Terminal分段滑模励磁控制器设计[J].
电工电能新技术, 2014, 33(6): 18-22, 35.
DOI:10.3969/j.issn.1003-3076.2014.06.004 |
| [8] |
杨培宏, 刘文颖, 魏毅立, 等. 基于自适应逆推变结构方法的非线性励磁控制[J].
电力系统保护与控制, 2012, 40(20): 125-144, 149.
DOI:10.7667/j.issn.1674-3415.2012.20.022 |
| [9] |
刘玲, 孙丽颖. 发电机励磁和SVC改进backstepping协调无源控制[J].
辽宁工业大学学报(自然科学版), 2016, 36(4): 211-215.
|
| [10] |
李帅兵, 董海鹰, 李晓青. 电励磁同步风力发电机输出电压DL-H∞控制
[J].
电气传动, 2015, 45(1): 64-68.
DOI:10.3969/j.issn.1001-2095.2015.01.014 |
| [11] |
常鲜戎, 张海生, 崔赵俊. 基于微分几何和扩张状态观测器的励磁控制[J].
电力系统及其自动化学报, 2015, 27(8): 87-91.
DOI:10.3969/j.issn.1003-8930.2015.08.016 |
| [12] |
肖健梅, 张科, 王锡淮. 基于预测函数与线性多变量反馈控制的同步发电机励磁控制[J].
电力自动化设备, 2015, 35(7): 153-159.
|
| [13] |
陈文韬, 王杰. 基于伪广义Hamilton理论的电力系统时滞反馈励磁控制[J].
电网技术, 2015, 39(8): 2238-2244.
|
| [14] |
李啸骢, 袁辉, 陈明媛, 等. 多机系统中STATCOM与发电机励磁的非线性分散协调控制设计[J].
电网技术, 2016, 40(8): 2350-2356.
|
| [15] |
谷志锋, 朱长青, 邵天章, 等. 全状态参数最优控制的鲁棒自适应励磁控制[J].
控制理论与应用, 2013, 30(7): 856-862.
|
| [16] |
谷志锋, 朱长青, 邵天章, 等. 含K类函数和附加控制量的自适应L2励磁控制
[J].
控制理论与应用, 2016, 33(2): 257-264.
|
| [17] |
梅生伟, 申铁龙, 刘康志. 现代鲁棒控制理论与应用[M]. 北京: 清华大学出版社, 2008: 307-308.
|
 2019, Vol. 45
2019, Vol. 45


