文章信息
- 李小亭, 郎月新, 韦子辉, 张要发, 杨泽, 徐潇潇
- LI Xiaoting, LANG Yuexin, WEI Zihui, ZHANG Yaofa, YANG Ze, XU Xiaoxiao
- 基于改进双向双边测距的超宽带定位技术及应用研究
- Research on UWB location technology and application based on improved symmetric double sided two-way ranging
- 中国测试, 2019, 45(10): 21-27
- CHINA MEASUREMENT & TEST, 2019, 45(10): 21-27
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018080074
-
文章历史
- 收稿日期: 2018-08-18
- 收到修改稿日期: 2018-11-16
目前GPS、北斗定位导航技术已获得广泛应用,但由于建筑物遮挡无法应用于室内环境。随着物联网技术的发展,定位导航技术必然由室外延伸到室内,目前谷歌、微软、苹果、博通等在内的一些科技巨头都开始布局室内定位技术。目前室内定位技术主要包括基于信号强度感知的WiFi、蓝牙、ZigBee,最高可实现3~5 m定位精度[1-3]。
为解决室内定位精度问题,IEEE802.15.4a-2007标准中建议采用信号飞行时间测量的定位技术,推荐的物理层通信技术为线性扫频扩频技术(chirp spread apectrum,CSS)和UWB定位技术[4-5]。无线信号频域越宽、时域越窄,则测距精度及抗干扰能力越强,UWB相对于CSS具有更高的带宽,因此UWB技术定位精度及抗多径干扰能力优于其他技术,目前超宽带定位技术已成为室内定位的首选技术方案[6]。
超宽带定位主要是采用TOF、到达时间差(time difference of arrial,TDOA)定位方式,TDOA定位需要精确的时钟同步,分为有线时钟同步和无线时钟同步两种方式,有线时钟同步需要设计同步信号装置,无线时钟同步需要设计时钟同步算法,设计实现较为复杂。而TOF定位采用双向双边测距测量标签到多个基站距离,基站无需时钟同步,多篇文献介绍了TOF的应用研究情况,卞佳兴等[7]分析了双向双边测距误差补偿机制,卢靖宇等[8]应用双向双边测距设计实现了一种机器人定位导航系统,TOF在多基站应用时,由于标签需要和相邻的多个基站测距,一次定位占用信道时间长,容易引起通信信号冲突。魏培等[9]提出了多基站测距和多标签调度机制,解决标签冲突和组网问题,设计了基于TOF的超宽带室内定位系统,并应用于工业车间现场。方文浩等[10]针对这一问题提出区域判定策略,标签通过判定所在区域,定位时只与区域内基站通信,避免重复地与未参与定位的基站建立连接,减少了节点间的无效通信。
TOF定位的主要缺点是定位时需要多次双向双边测距,导致定位速度慢、标签功耗大、与多基站测距时产生通信冲突。文献[9-10]主要通过设计调度机制减少通信冲突,并没有提高定位速度。本文提出一种改进双向双边测距算法,一次双向双边测距即可测量标签到多个基站的距离、实现定位,大幅度提高了TOF定位速度,并采用Decawave公司的DW1000芯片设计了超宽带定位实验系统,对该方法进行测试及实验验证。
1 TOF定位技术与TDOA定位技术TOF定位技术是通过测量无线信号的传播时间来计算移动节点和固定节点间的距离。为减小晶振误差造成的时间测量误差,在IEEE802.15.4a-2007标准中建议采用双向双边测距方法通过差分运算提高测距精度[5]。
通过差分运算可有效消除晶振误差引起的时间测量误差。使得通信节点在采用普通精度晶振的情况下,仍可获得较高的时间测量精度。但双向双边测距的主要缺点是需要多次收发无线信号完成测距,所需时间长。而一次二维定位至少需要三次测距,导致定位标签功耗高,定位速度慢,容量小。这一缺点极大地限制了TOF定位的应用,目前在定位领域广泛采用的是TDOA定位,TDOA定位只需标签发射一次信号,即可实现定位,定位速度远高于TOF定位,但TOF定位在定位区域和三维定位方面优于TDOA,在某些应用场合TDOA定位无法代替TOF定位[11]。
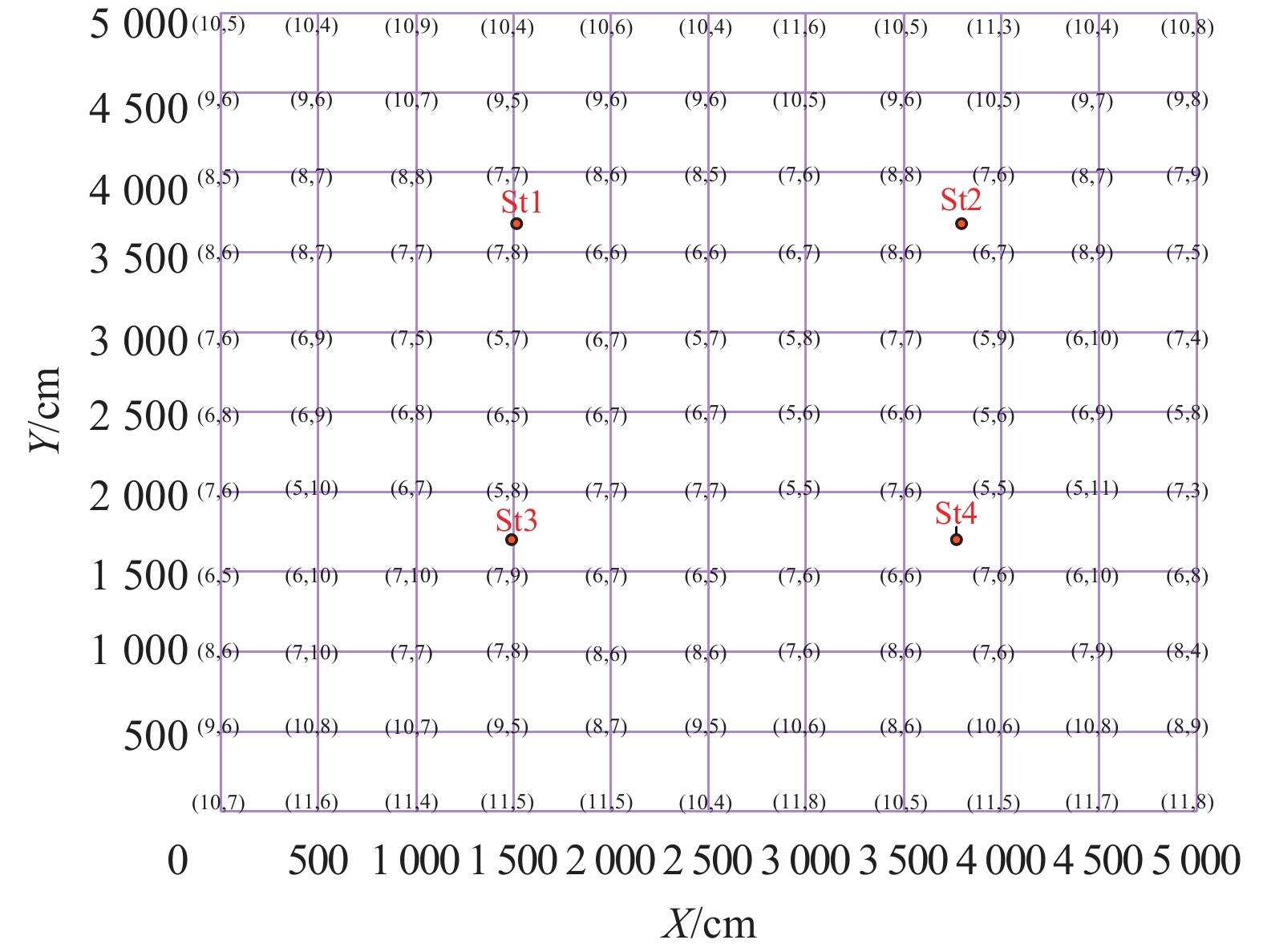
图1为仿真计算得到的TOF定位误差区域分布,St1、St2、St3、St4为定位基站,图中选择一点,计算得到该点到基站的距离,加上标准差为10的高斯噪声,由距离求解非线性方程组计算坐标,并通过100次仿真计算统计加上测距噪声的TOF定位误差,图形中的数字表示该点的TOF定位(X,Y)定位坐标误差标准差,由图1可见TOF定位基站区域外和区域内定位精度变化不大。
|
| 图 1 TOF定位区域误差分布 |
同样过程对TDOA定位误差进行仿真计算,采用泰勒级数展开法求解距离差的非线性方程组,图2为TDOA定位误差区域分布,可见基站区域外定位误差明显增大。因此同样基站布局,TOF定位可定位范围优势明显。另一方面TOF定位三维定位优于TDOA定位,TDOA定位为实现高度方向的距离差测量,必须要求基站安装存在高度差,且高度差越大高度方向上的定位误差越小,造成实际应用中安装部署困难,而TOF定位不存在这个问题。基站安装在同一水平面也可实现三维定位。

|
| 图 2 TDOA定位区域误差分布 |
综合以上分析TOF定位在定位区域,三维定位方面优于TDOA定位,TOF定位不需要时钟同步,较TODA更容易实现,但定位速度慢是其主要缺点,这也限制了TOF定位的应用。
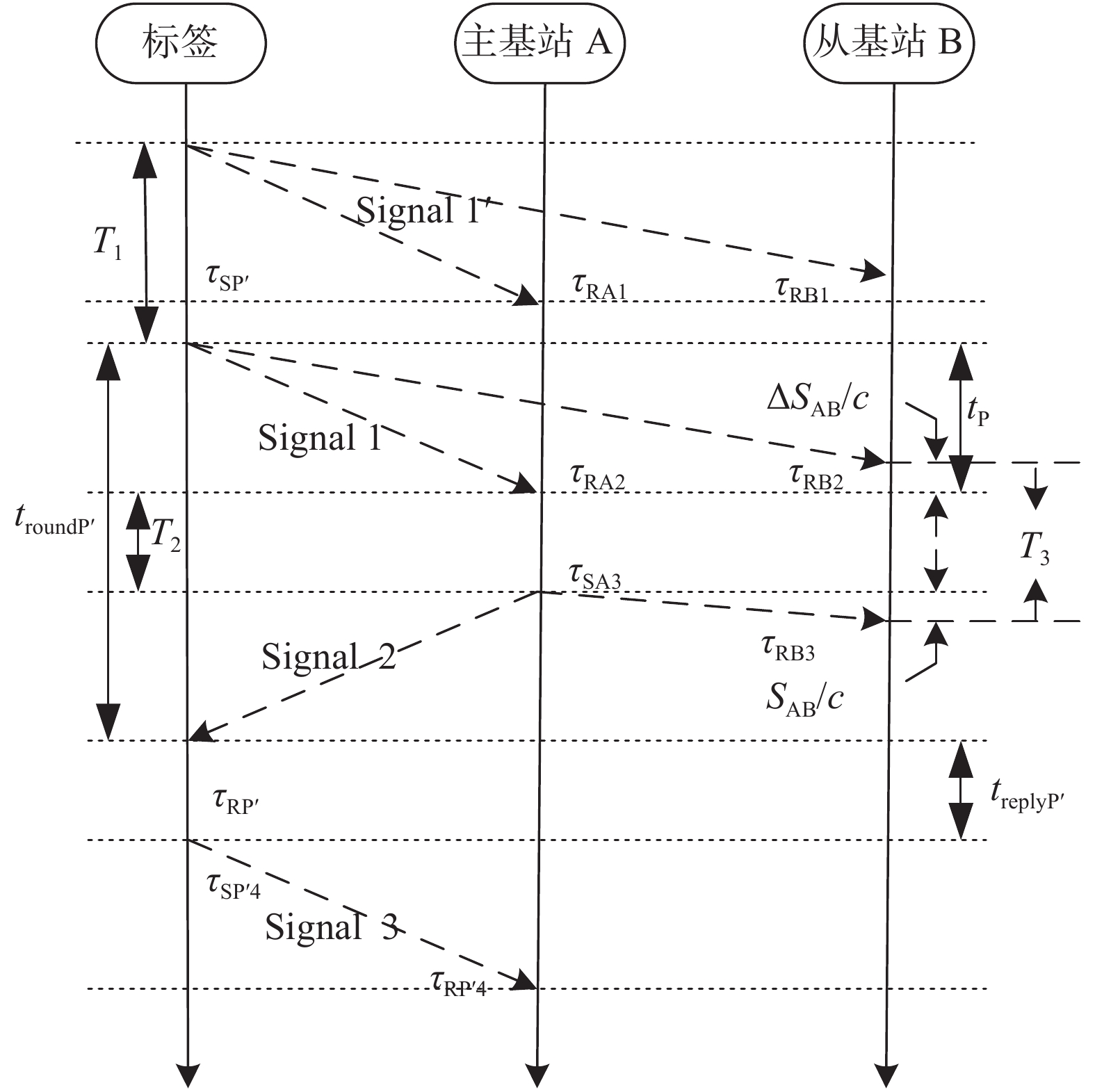
2 改进双向双边测距算法针对TOF定位速度慢的问题,在双向双边测距算法基础上改进算法,图3中所示标签与主基站A双向双边测距的同时,实现标签到主基站A和从基站B的距离差测量,通过距离和距离差计算标签到从基站的距离。
|
| 图 3 改进双向双边测距算法示意图 |
如图3所示,双向双边测距算法由Signal 1、Signal 2、Signal 3的发送接收完成,实现标签到主基站A的测距,在双向双边测距前标签先发送一次广播信号Signal 1',基站A、B均收到信号标签发送的信号Signal 1'、Signal 1,从基站B也收到基站A发送的回复信号Signal 2。根据上述几个信号接收时间值,即可计算标签(Tag)到基站A、B的距离差。具体推导过程如下。
假设移动节点Tag到A、B基站的距离均不相等,所以A、B 4个固定参考节点接收到信号1和信号2的时间也是不一样的,其差值为
| $k = \frac{{({\tau _{\rm RA2}} - {\tau _{\rm RA1}})}}{{({\tau _{\rm RB2}} - {\tau _{\rm RB1}})}}$ | (1) |
主基站A接收两次广播信号Signal 1'和Signal 1后,根据时间间隔测量值
如图3所示,
| $({\tau _{\rm RB3}} - {\tau _{\rm RB2}}) \times k$ | (2) |
| ${T_3} = \frac{{\Delta {S_{\rm AB}}}}{c} + \frac{{{S_{\rm AB}}}}{c} + {T_2}$ | (3) |
| ${T_2} = {\tau _{\rm SA3}} - {\tau _{\rm RA2}}$ | (4) |
计算A,B两节点接收信号的时间差为:
| $ \frac{{\Delta {S_{\rm AB}}}}{c} = ({\tau _{\rm RB3}} - {\tau _{\rm RB2}}) \times k - ({\tau _{\rm SA3}} - {\tau _{\rm RA2}}) - \frac{{{S_{\rm AB}}}}{c} $ | (5) |
通过Tag和基站A、B之间的信号Signal 1'、Signal 2、Signal 3发送接收时间测量即可实现Tag和基站A、B的距离差
| ${S_{\rm B}} = {S_{\rm A}} - \Delta {S_{\rm AB}}$ | (6) |
在从基站B的测距过程中,从基站B只接收信号,因此可以任意增加从基站的个数。采用一次改进双向双边测距,测量标签到主基站距离的同时,完成标签到多个从基站距离测量,并且只是增加了一次信号发送,未增加过多通信开销,实际应用中可大幅提高TOF定位速度。对于四基站TOF定位,定位时间缩短至原定位时间的1/4。
3 UWB定位实验系统设计为验证算法可行性,设计UWB定位实验系统,平台节点采用Decawave公司推出的基于IR-UWB通信技术的DW1000射频芯片,典型带宽500 MHz。采用脉冲位置调制和二进制相移键控调制方式。DW1000发射功率调整范围−62~−35 dBm/MHz,采用双向双边测距方法时110 kb/s通信速率最大测距距离为290 m,最高可实现0.1 m测距精度,最大通信速率为6.8 Mb/s。DW1000芯片内部集成63.8976 GHz采样时钟,计时单位为15.65 ps,保证了测距过程中的时间测量精度。发送数据帧格式参照IEEE802.15.4-2011标准,包括前导码(preamble code)、数据帧分隔符(start of frame delimiter,SFD)、数据帧头(physical layer header,PHR)、数据区部分。芯片在发送数据时,可以记录发送数据中PHR首字符发出时的时钟计数,同样接收时也可以测量记录接收数据PHR首字符到达的采样时钟计数。测量精度达到100~150 ps[6]。
DW1000可以采用延时发送机制,根据当前时钟计数,设定延时时间,可以精确计算将要发送数据PHR首字符发出时的时钟计数,并可将该时钟计数值加入到数据包中,进而发送给接收方。以上功能保证了DW1000可以用来实现测量信号到达时间以及进行双向双边测距的目的。
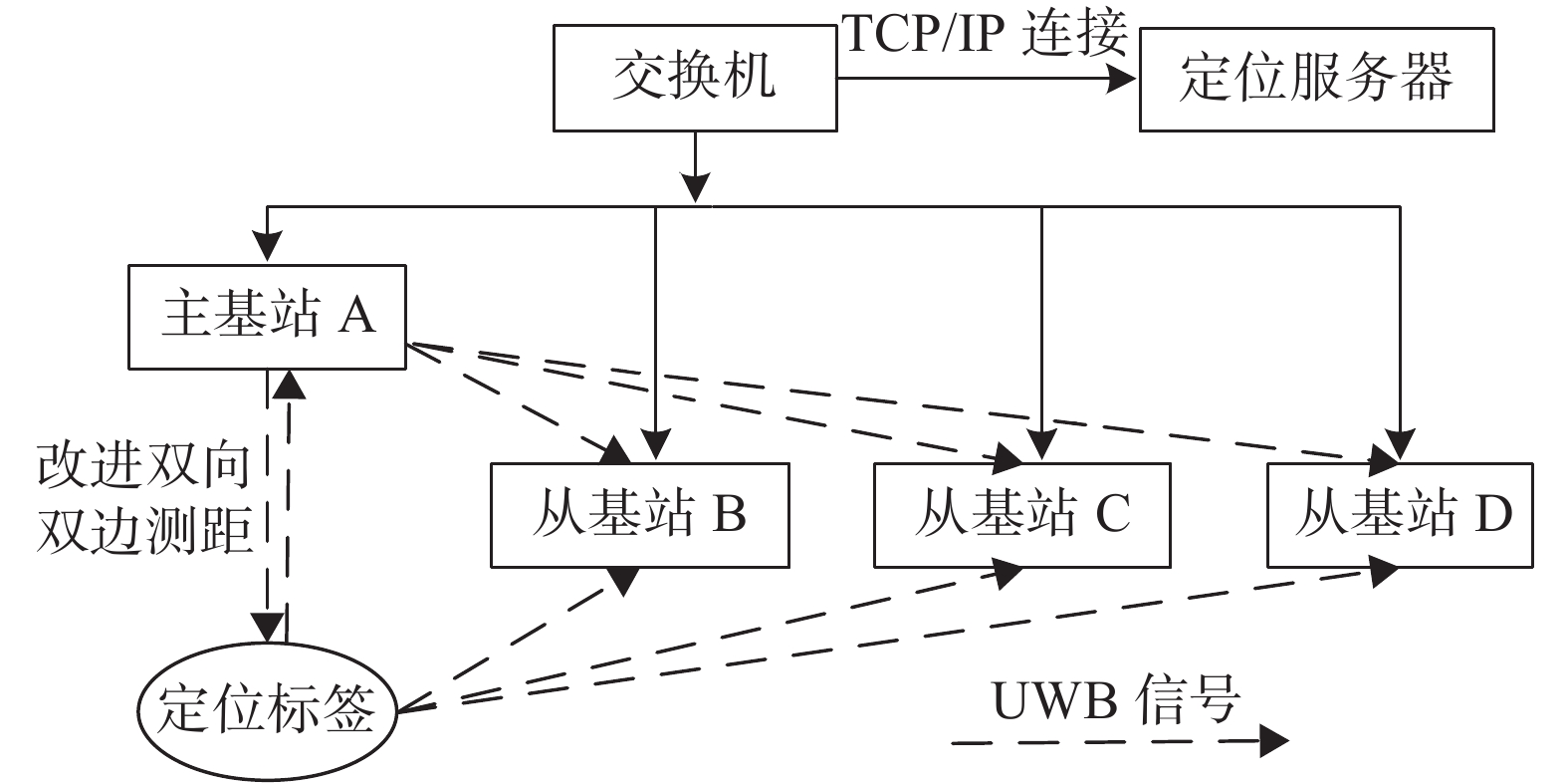
UWB定位系统如图4所示,由标签、基站、定位坐标计算服务器三层架构组成,标签、基站均采用DW1000芯片,标签设计考虑低功耗,采用MSP430系列单片机作为主控制器,基站采用Stm32处理器。定位基站通过交换机建立的局域网与定位服务器连接,通过TCP/IP协议与定位服务器实现数据传输。
|
| 图 4 UWB定位实验平台框架示意图 |
TOF定位算法需要测量标签到各固定基站的距离,由标签发起与主基站A的改进双向双边测距,同时完成距离差测量,如图4所示测距过程中从基站只接收数据,因此从基站个数不受限制。各基站测量数据汇总到定位服务器,计算标签到各从基站的距离,并通过求解非线性方程组计算定位坐标。
4 精度测试在上述测试平台下,采用改进双向双边测距实现TOF定位,为缩短测距时间DW1000采用6.8 Mb/s通信速率,完成一次改进双向双边测距所需时间在1.8 ms以内。如图5所示,在室内环境

|
| 图 5 UWB室内定位测试环境 |
表1为标签在改进双向双边测距法下测得的距离值测量误差。将标签放置于选定测量点可得到主基站和各个从基站到标签的距离标准差平均值,到从基站距离值由于距离差测量引入新的误差,可以看出,标签到从基站测距值标准差稍大。同时表中列出了各测距值的绝对偏差平均值,测距值均大于真实值,经过仔细校准后绝对偏差可进一步缩小。
| cm | |||
| 到主基站A测距值标准差平均值 | 到从基站B测距值标准差平均值 | 到从基站C测距值标准差平均值 | 到从基站D测距值标准差平均值 |
| 2.6 | 12.5 | 10.7 | 10.5 |
| 到主基站A绝对偏差平均值 | 到从基站B绝对偏差平均值 | 到从基站C绝对偏差平均值 | 到从基站D绝对偏差平均值 |
| 11.5 | 23.0 | 7.8 | 11.7 |
表2中列出所选取9点的定位误差。定位标准偏差绝大多数在10 cm以内,绝对偏差略大在30 cm左右。图6为标签刷新率为40 Hz时的室内定位轨迹,定位轨迹较好反映了实际轨迹,可满足大多数室内定位应用精度要求。
| cm | |||
| 标签位置的
标定真值/cm |
标签定位
平均值 |
X坐标的
标准差 |
Y坐标的
标准差 |
| (80,80) | (55.9,79.5) | 8.9 | 8.7 |
| (80,240) | (45.9,253.5) | 10.1 | 5.0 |
| (80,400) | (51.4,426.7) | 12.1 | 6.5 |
| (240,80) | (238.1,76.1) | 5.4 | 7.8 |
| (240,240) | (226.3,260.0) | 7.6 | 5.6 |
| (240,400) | (230.9,420.8) | 7.2 | 4.2 |
| (400,80) | (409.5,74.8) | 4.2 | 8.8 |
| (400,240) | (403.5,244.5) | 5.3 | 6.9 |
| (400,400) | (399.2,407.2) | 5.9 | 4.8 |

|
| 图 6 室内定位轨迹 |
图6在
随着人们生活水平提高,游乐设施行业得到了快速发展。同时,游乐设施关系到游客的安全,越来越受到人们的重视。过山车是一种依靠重力运行的游乐设施,最高速度可达100 km/h。在开始运行阶段,机械装置将过山车送至最高点,之后,过山车依轨道实现自运行。由于轨道复杂、速度大,需要检测过山车运动参数(比如速度、加速度),以保障游客安全。
5.1 基于超宽带定位技术的过山车速度检测方案过山车运行区间大、运行速度快、运行轨迹复杂,普通过山车高度可达30~50 m。传统的测速方法如雷达测速等方法不能满足要求。由于超宽带具有抗多径干扰、定位精度高的优点,在复杂环境下也能保持良好定位精度,因此可应用超宽带定位技术通过三维定位计算过山车轨迹、速度、加速度。由于过山车运行快,最快时速达到百公里以上,对过山车进行测速,要求较高的定位刷新率。
采用改进双向双边测距的TOF定位算法只需一次测距就可以实现移动节点到多个固定参考节点的测距,提高了TOF定位刷新率,并且4个基站可以部署在同一水平面即可实现三维测速,安装方便。综合以上分析,可将改进双向双边测距的TOF定位算法应用于过山车测速中。
5.2 测速方案实施选取装备过山车的游乐园作为试验场所。在过山车运行前,将定位标签稳固在过山车座位上方(见图7),避免信号遮挡增加测试准确度。过山车高速运行过程中有两种典型运动,一种是从高处滑下的下落运动,另一种是在圆轨道上翻滚运动。在此选取高速下落运动进行定位测速分析。

|
| 图 7 定位标签固定图 |
根据实地搭建测速环境,4个基站定位区域为50 m×20 m,基站布置在覆盖测试段长方形区域各个顶角处。4个定位基站、载有标签的过山车和定位坐标计算服务器一起构成了超宽带定位系统。当附有标签的过山车经过4个基站覆盖的测试区域时,系统根据测量数据计算过山车的运动轨迹和速度。
5.3 基于卡尔曼滤波算法的数据处理利用超宽带系统采集的位置坐标信息可以绘出过山车从高处下落的轨迹,为提高测量的精度,采用卡尔曼滤波对测量数据进行处理。如图8所示,是以卡尔曼滤波算法为基础的整体结构流,将测量数据导入卡尔曼滤波器,并对初始位置信息等滤波器参数设置以达到理想要求[12]。

|
| 图 8 整体结构图 |
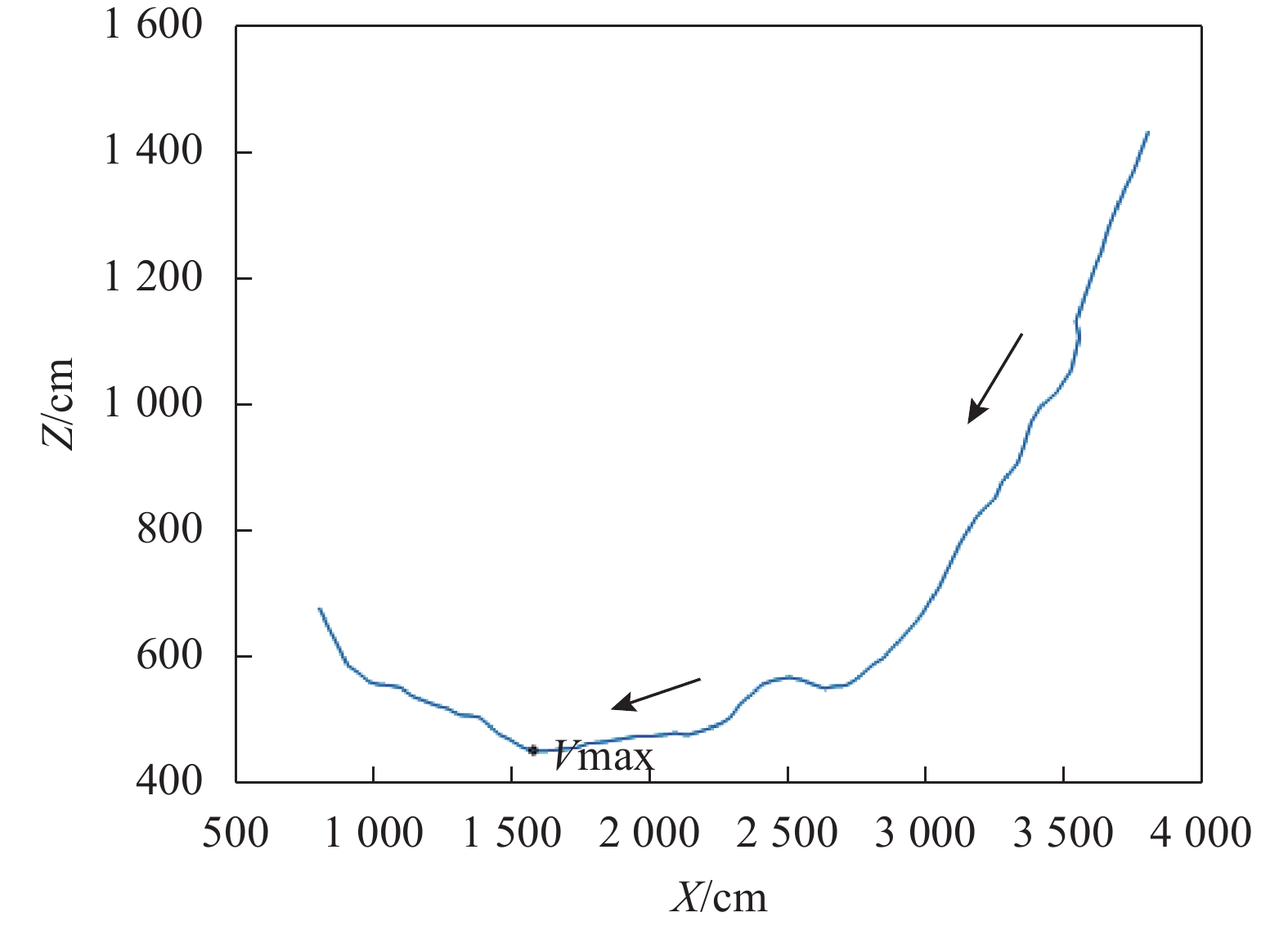
利用超宽带系统采集的位置坐标信息可以绘出过山车从高处下落的轨迹如图9、图10所示。比较两幅图可以看出,经过卡尔曼滤波处理的轨迹相对于原始轨迹图更光滑,降低了不确定的干扰,确保收集到的位置坐标信息能真实反映过山车的实际运行状态。由经过卡尔曼滤波处理后的轨迹可以看出,过山车从最高端落下经过最低点后又上滑一段,在轨迹最底端有最大速度值。
|
| 图 10 过山车从高处下落滤波后的轨迹图 |
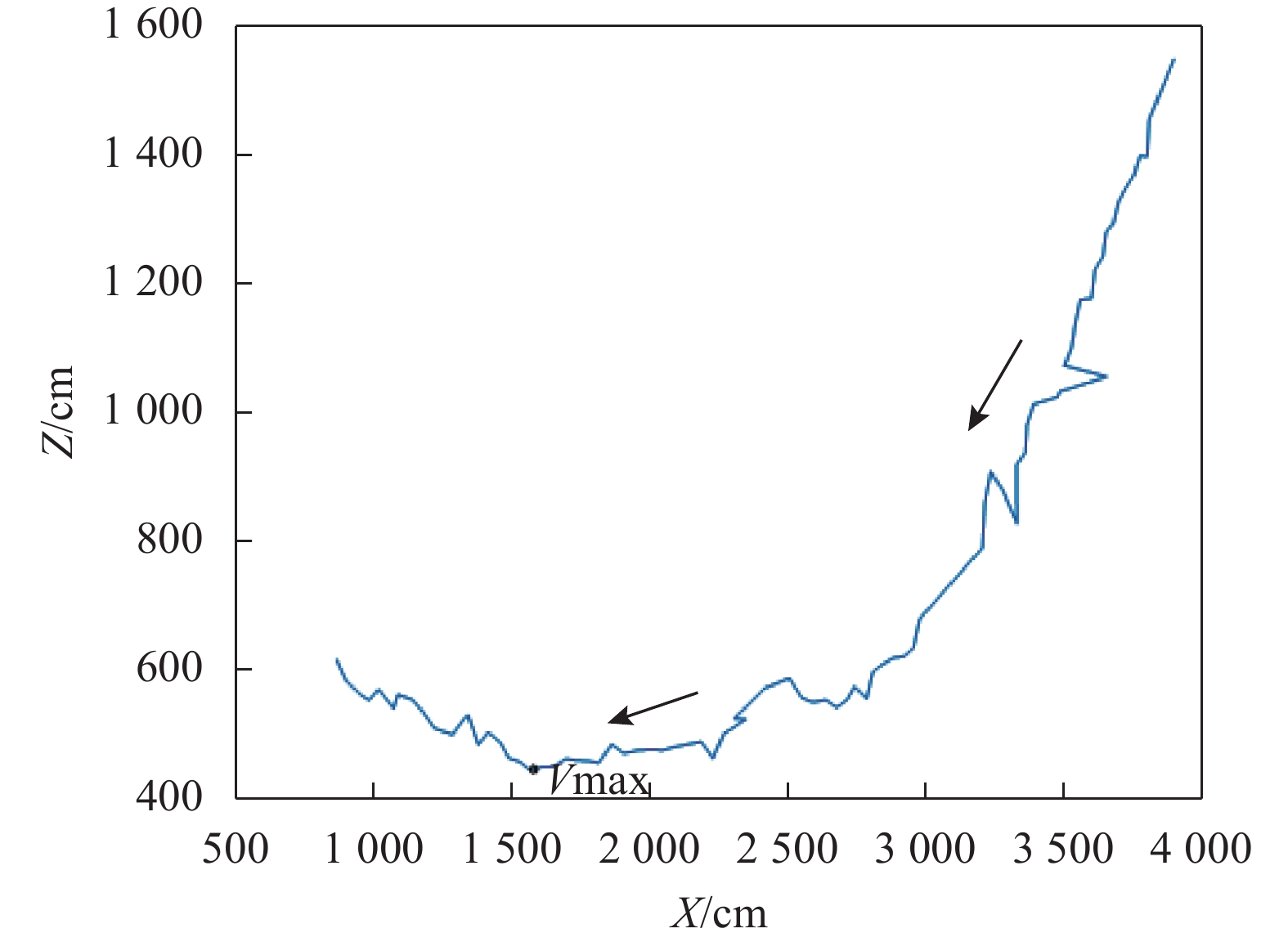
|
| 图 9 过山车从高处下落滤波前的轨迹图 |
同样,利用过山车位置坐标信息可以绘出过山车从高处下落的速度图,通过图11、图12可以看出,卡尔曼滤波后的速度图与滤波前速度图比较更有规律性。观察滤波后的速度图,过山车从高处落下时具有初始速度,速度随下落距离增大而增大,到达底端获得最大速度约87km/h。测量得到的轨迹和速度与厂家给出的数据基本吻合,说明了该方法的实用性。

|
| 图 11 过山车从高处直接下落卡尔曼滤波前的速度图 |

|
| 图 12 过山车从高处直接下落卡尔曼滤波后的速度图 |
6 结束语
TOF定位在定位区域、三维定位方面优于TDOA定位,TOF定位不需要时钟同步,较TDOA更容易实现,但定位速度慢限制了TOF定位的应用,采用改进双向双边测距的TOF定位可大幅提高TOF定位速度,采用四基站时,定位时间约为原定位时间的1/4,并且经实验验证可实现分米级的定位精度。为提高测量精度,结合UWB定位技术,用改进双向双边测距的TOF定位在过山车测速中的测量方案进行设计,将卡尔曼滤波算法应用于过山车定位数据处理中。在游乐园里对过山车进行实验,结果显示该定位技术能够较好地完成对高速运动物体速度的测量,具有很好的应用前景。
| [1] |
卢伟军, 孙希延, 纪元法, 等. GPS伪卫星高精度室内定位技术研究与实现[J].
电子技术应用, 2018, 44(3): 36-39.
|
| [2] |
裴凌, 刘东辉, 钱久超. 室内定位技术与应用综述[J].
导航定位与授时, 2017, 4(3): 1-10.
|
| [3] |
阮陵, 张翎, 许越, 等. 室内定位: 分类、方法与应用综述[J].
地理信息世界, 2015, 22(2): 8-14.
DOI:10.3969/j.issn.1672-1586.2015.02.002 |
| [4] |
陈新科, 喻川, 文智力. UWB定位技术在煤矿井下的应用[J].
煤炭科学技术, 2018, 46(S1): 187-189.
|
| [5] |
IEEE Computer Society. Wireless medium access control (MAC) and physical layer (PHY) specifications for low-rate wireless personal area networks (WPANs): IEEE Standard 802.15.4a-2007[S]. New York: IEEE, 2007.
|
| [6] |
韦子辉, 冯正和, 王志峰. 脉冲超宽带定位单元设计及应用测试[J].
电视技术, 2014, 38(23): 60-63.
DOI:10.3969/j.issn.1002-8692.2014.23.016 |
| [7] |
卞佳兴, 朱荣, 陈玄. 基于改进双向测距到达时间差定位算法的超宽带定位系统[J].
计算机应用, 2017, 37(9): 2496.
DOI:10.11772/j.issn.1001-9081.2017.09.2496 |
| [8] |
卢靖宇, 余文涛, 赵新. 基于超宽带的移动机器人室内定位系统设计[J].
电子技术应用, 2017, 43(5): 23-28.
|
| [9] |
魏培, 姜平, 贺晶晶, 等. 基于内三角形质心算法的超宽带室内定位[J].
计算机应用, 2017, 37(1): 289-293.
|
| [10] |
方文浩, 陆阳, 卫星. 基于区域判定的超宽带井下高精度定位[J].
计算机应用, 2018(3): 1-7.
DOI:10.3969/j.issn.2095-347X.2018.03.001 |
| [11] |
FRESNO J M, ROBLES G, MARTÍNEZ-TARIFA J M, et al. Survey on the performance of source localization algorithms[J].
Sensors (Basel), 2017, 17(11): 2666.
DOI:10.3390/s17112666 |
| [12] |
梁民赞, 黄子豪, 曹占启. 曲线拟合与卡尔曼滤波器的滤波精度评估[J].
无线电工程, 2013, 43(3): 36-39.
DOI:10.3969/j.issn.1003-3106.2013.03.011 |
 2019, Vol. 45
2019, Vol. 45




