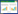文章信息
- 邓鹰飞, 刘桂雄
- DENG Yingfei, LIU Guixiong
- 基于扩展收敛域指数CORDIC算法的超声时间增益补偿技术
- Ultrasonic time gain compensation technology based on extended convergence index CORDIC algorithm
- 中国测试, 2018, 44(7): 116-120
- CHINA MEASUREMENT & TEST, 2018, 44(7): 116-120
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018.07.022
-
文章历史
- 收稿日期: 2018-01-03
- 收到修改稿日期: 2018-02-26
2. 华南理工大学机械与汽车工程学院,广东 广州 510640
2. School of Mechanical and Automotive Engineering, South China University of Technology, Guangzhou 510640, China
超声相控阵技术是工业无损检测领域中极为重要的手段[1- 2],可灵活控制声束形状、焦点位置和扫查路径等。在相控阵检测中,超声信号强度会随其在介质中传播而衰减,影响检测图像质量,需对回波信号进行时间增益补偿(TGC),而基于传统串行处理的CPU或数字信号处理技术(DSP)难以满足相控阵大量数据实时处理要求。故本文将解决三角函数、指数函数等运算的经典CORDIC算法[3- 4]用于超声相控阵时间增益补偿,研究指数CORDIC算法收敛域扩展方法及其FPGA实现技术,并采用该算法计算超声相控阵时间增益(dB)曲线对应的原始放大倍数,设计基于CORDIC算法的dB-倍数求解器,实现超声回波信号的实时、高精度补偿,最后对超声TGC系统性能进行仿真和试验。
1 指数CORDIC算法原理及收敛域扩展指数CORDIC算法仅通过移位、加减操作即可实现对指数函数求解,但该算法收敛域太小,因此需研究其收敛域扩展方法才能使之满足工业应用需求。
1.1 指数CORDIC算法原理图1为双曲系统向量旋转模型图,向量
| $\left\{ \begin{aligned}{x_n} = C \cdot \cosh (\lambda + \varTheta ) = {x_1}\cosh \varTheta + {y_1}\sinh \varTheta \\{y_n} = C \cdot \sinh (\lambda + \varTheta ) = {x_1}\sinh \varTheta + {y_1}\cosh \varTheta \end{aligned} \right.$ | (1) |
|
| 图 1 双曲系统CORDIC旋转模型 |
若将
| $\begin{aligned}\left( \begin{aligned}{x_n}\\{y_n}\end{aligned} \right) = \prod\limits_{i = 1}^n {\left\{ {{\rm cosh}{\theta _i} \cdot \left( \begin{aligned}1\;\;\;{\rm tanh}{\theta _i}\\{\rm tanh}{\theta _i}\;\;\;1\;\end{aligned} \right) \cdot \left( \begin{aligned}{x_1}\\{y_1}\end{aligned} \right)} \right\}} =\quad\quad\quad\quad \\ \prod\limits_{i = 1}^n {\left\{ {\left( \begin{array}{l}1\;\;\;\;\;{d_i} \cdot {2^{ - i}}\\{d_i} \cdot {2^{ - i}}\;\;\;\;1\end{array} \right) \cdot \left( \begin{aligned}{x_1}\\{y_1}\end{aligned} \right) \cdot K} \right\}} \quad\quad\quad\quad\quad\;\; \\K = \prod\limits_{i = 1}^n {{\rm cosh}{\theta _i}} = \prod\limits_{i = 1}^n {\sqrt {\frac{1}{{1 - {\rm tanh}{^2}{\theta _i}}}} } = \prod\limits_{i = 1}^n {\sqrt {\frac{1}{{1 - {2^{ - 2i}}}}} } \end{aligned}$ | (2) |
其中K是缩放因子,当向量旋转次数足够多时,它趋于一个常数1.207 5。
指数CORDIC算法每次旋转迭代方程式为
| $\left\{ \begin{aligned}{x_i}_{ + 1} = {x_i} + {d_i}{y_i}{2^{ - i}} \quad\;\; \\{y_i}_{ + 1} = {y_i} + {d_i}{x_i}{2^{ - i}} \quad\;\; \\{z_i}_{ + 1} = {z_i} - {d_i}{\tanh ^{ - 1}}{2^{ - i}}\\{d_i} = {\rm sign}({z_i}) \quad\quad\quad\end{aligned} \right.$ | (3) |
要满足迭代收敛,必须在第一次迭代之后,每隔3次迭代,重复一次当前旋转角度[6- 7],即i=1, 2, 3, 4, 4, 5, 6, 7, 7,···, n。
若初始输入x1=y1=1/K,zin=
| $\begin{aligned}\left\{ \begin{aligned}{x_{n + 1}} = K[{x_1}\cosh ({z_{{\rm in}}}) + {y_1}\sinh ({z_{{\rm in}}})]\\{y_{n + 1}} = K[{x_1}\sinh ({z_{{\rm in}}}) + {y_1}\cosh ({z_{{\rm in}}})]\\{z_{n + 1}} = 0 \quad\quad\quad\quad\quad\quad\quad\quad\quad\quad\end{aligned} \right.\\ \Rightarrow {x_{n + 1}} = {y_{n + 1}} = \cosh {z_{{\rm in}}} + \sinh {z_{{\rm in}}} = {{\rm e}^{{z_{{\rm in}}}}} = {{\rm e}^\theta }\end{aligned}$ | (4) |
即可求出
由双曲系统指数CORDIC算法原理及角度序列表达式可知,若旋转向量一直往同一个方向迭代,可得到CORDIC算法能够计算的最大输入角度,即双曲线系统CORDIC算法的收敛范围:
| $|{z_{\rm{in}}}| \leqslant {\theta _{\rm{max}}} = \sum\limits_{i = 1}^N {{\rm{tan{h^{ - 1}}}}({2^{ - i}}){|_{N = \infty }}} \approx 1.118\;2$ | (5) |
由于算法收敛范围太小,无法满足超声相控阵时间增益控制系统信号处理需求,因此需对算法收敛域进行扩展处理。
对任意输入角度
| ${z_{\rm{in}}} = Q \cdot \ln 2 + \varphi \Rightarrow {{\rm e}}^{{z_{\rm{in}}}} = {2^Q} \cdot {\rm e^\varphi }(\varphi < \ln 2)$ | (6) |
故只需用CORDIC算法求得
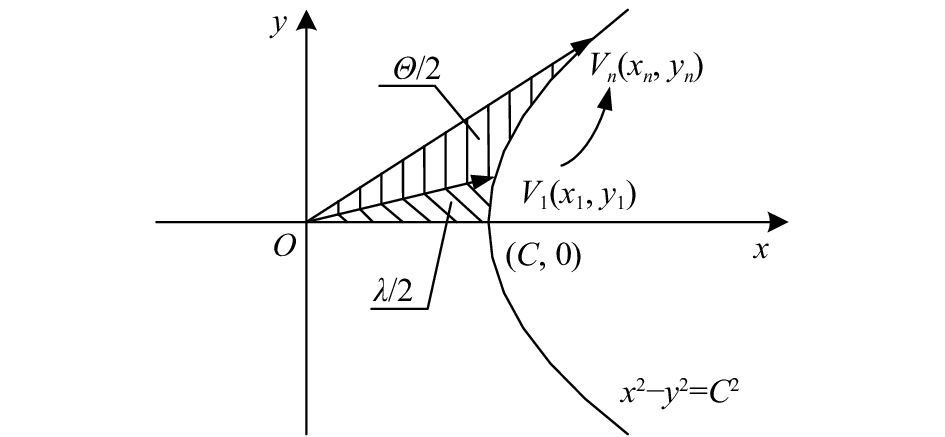
图2为基于CORDIC算法的超声时间增益补偿原理图。首先读取存储在系统RAM中dB形式的增益曲线,通过扩展收敛域指数CORDIC算法计算其原始放大倍数G(t),再通过乘法器组将A/D采样后超声回波数字信号与放大倍数相乘,最后经D/A转换器输出补偿后的模拟信号。本方法的重点在基于CORDIC算法的dB-倍数求解器设计 、超声时间增益补偿FPGA实现。
|
| 图 2 基于CORDIC算法的超声时间增益控制原理图 |
2.2 基于CORDIC算法的dB-倍数求解器设计及仿真
图3为基于指数CORDIC算法的dB-倍数求解器原理图。将上位机软件生成的分贝数增益曲线转化为原始放大倍数曲线的计算速度、精度,设计基于扩展收敛域指数CORDIC算法的dB-放大倍数对应求解器,把对应不同深度检测位置的dB补偿增益实时转化为原始放大倍数,对超声回波信号进行数字补偿,提高增益范围、精度。其中dB-倍数对应求解器输入参数应为检测材料的衰减系数、当前聚焦检测深度(由上位机软件输入)。

|
| 图 3 基于CORDIC算法的dB-倍数求解器原理图 |
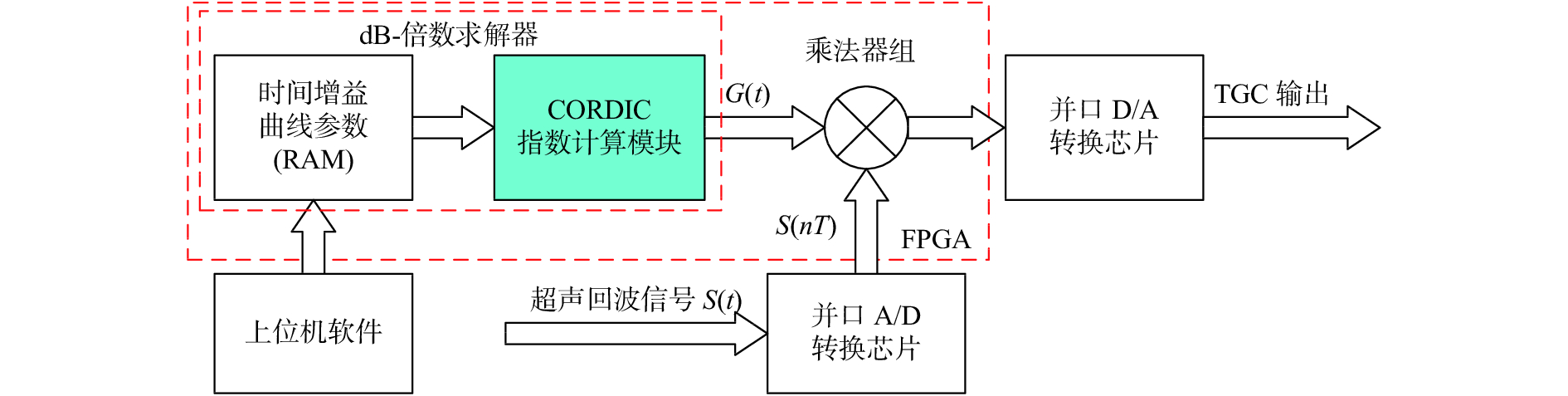
在Matlab上对基于指数CORDIC算法的dB-倍数求解器进行精度仿真,图4为基于CORDIC算法的dB-倍数求解器仿真结果。图4(a)是根据平面波超声信号在均匀介质中衰减情况模拟出的超声信号衰减曲线,再通过扩展收敛域指数CORDIC算法计算得到相应的回波信号实际增益补偿曲线,图中左纵坐标y表示衰减倍数,右纵坐标G(t)表示经CORDIC算法计算得到的超声回波实际增益系数。模拟超声检测系统参数为:介质衰减系数
|
| 图 4 CORDIC算法dB-倍数求解器仿真结果图 |
2.3 超声时间增益补偿FPGA实现及仿真
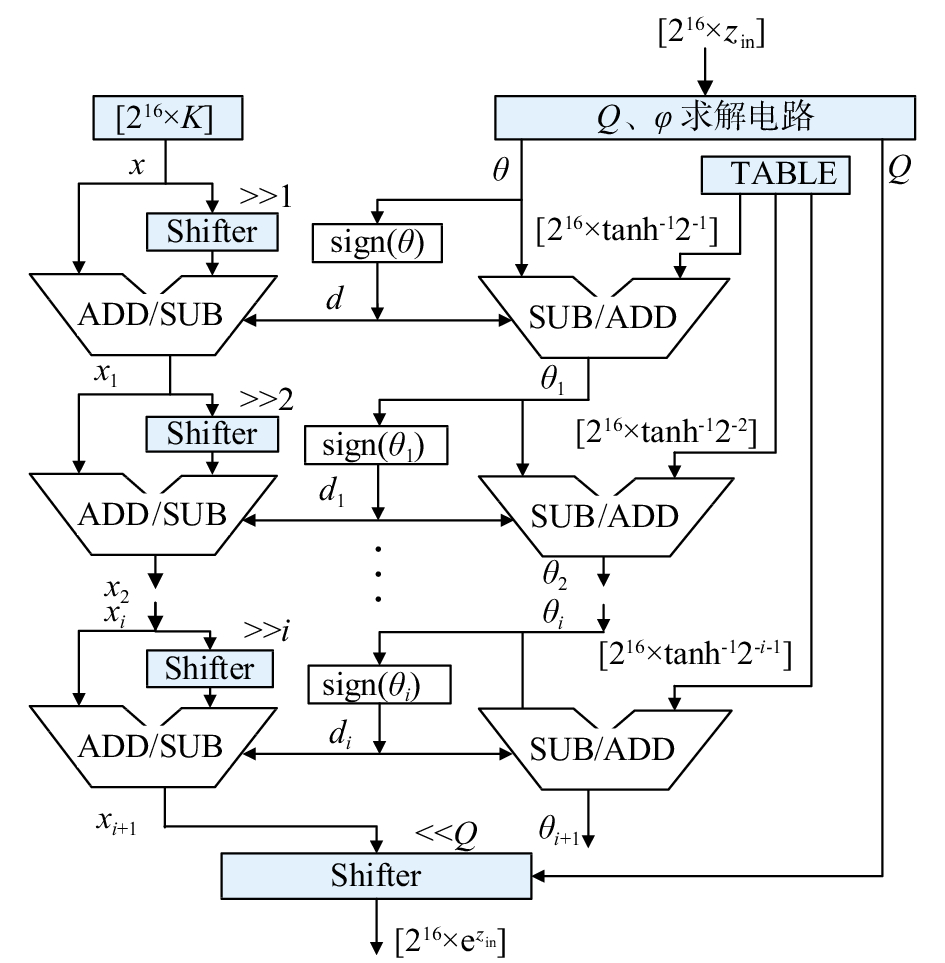
为加快超声相控阵时间增益控制系统运算速度,可采用流水线设计法在FPGA上实现扩展收敛域指数CORDIC算法,如图5所示。
|
| 图 5 指数CORDIC算法FPGA实现图 |
本文采用FPGA开发编程软件Quartus Ⅱ进行仿真,选用芯片为Cyclone Ⅳ系列EP4CE15F17A7,仿真时钟频率为100 MHz。为验证CORDIC算法在FPGA上计算指数函数输出精度,在Modelsim软件上对CORDIC算法指数计算模块进行编译仿真。采用15级流水线CORDIC算法结构,将Modelsim仿真数据导出分析,取部分浮点求其指数的仿真计算结果,并与实际值进行对比,如表1所示。
可以看出,算法在FPGA上实现计算指数函数平均最大相对误差不超过0.01%,足以满足超声相控阵时间增益补偿系统精度的要求。
|
|
|
|
相对误差/% |
| 0.5 | 1.648 72 | 1.648 81 | 0.005 5 |
| 1.5 | 4.481 68 | 4.481 43 | –0.005 6 |
| 2.5 | 12.182 49 | 12.181 98 | –0.004 2 |
| 3.5 | 33.115 45 | 33.115 81 | 0.001 1 |
| 4.5 | 90.017 13 | 90.018 02 | 0.001 0 |
| 5.5 | 244.691 93 | 244.690 95 | –0.000 4 |
| 6.5 | 665.141 63 | 665.139 49 | –0.000 3 |
| 7.5 | 1 808.142 41 | 1 808.145 88 | 0.000 2 |
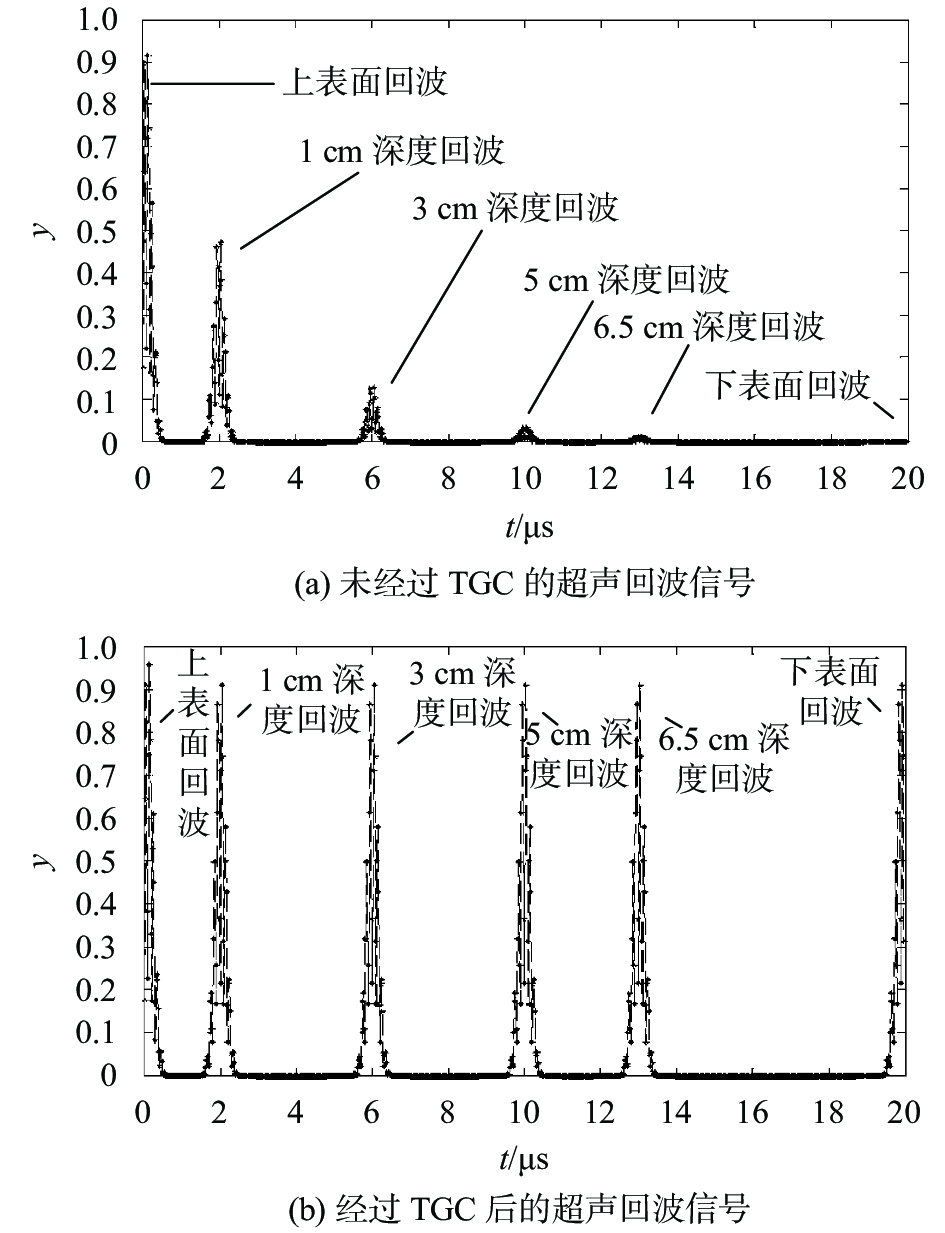
在Matlab上对基于指数CORDIC算法的超声相控阵时间增益控制系统工作情况进行仿真。模拟超声检测参数分别为:探头中心频率5 MHz,采样频率50 MHz,被测物体(固)厚度10 cm,超声波速5 000 m/s,介质衰减系数
|
| 图 6 基于CORDIC算法的超声回波增益补偿仿真 |
3 基于CORDIC算法的超声时间增益补偿试验
本文具体试验方案为:在超声相控阵上位机软件上根据被测材料输入其声波衰减系数
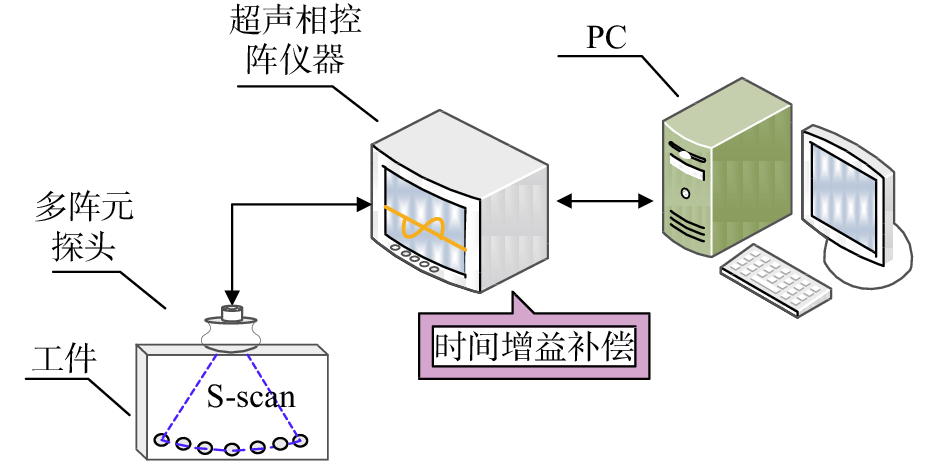
图7为搭建的试验平台,采用超声相控阵仪器作为下位机,基于FPGA+CORDIC算法实现模式,实现超越函数CORDIC算法硬件求解。检测对象为B型标准试块纵向分布的8个直径为2 mm的圆孔。
|
| 图 7 试验平台搭建图 |
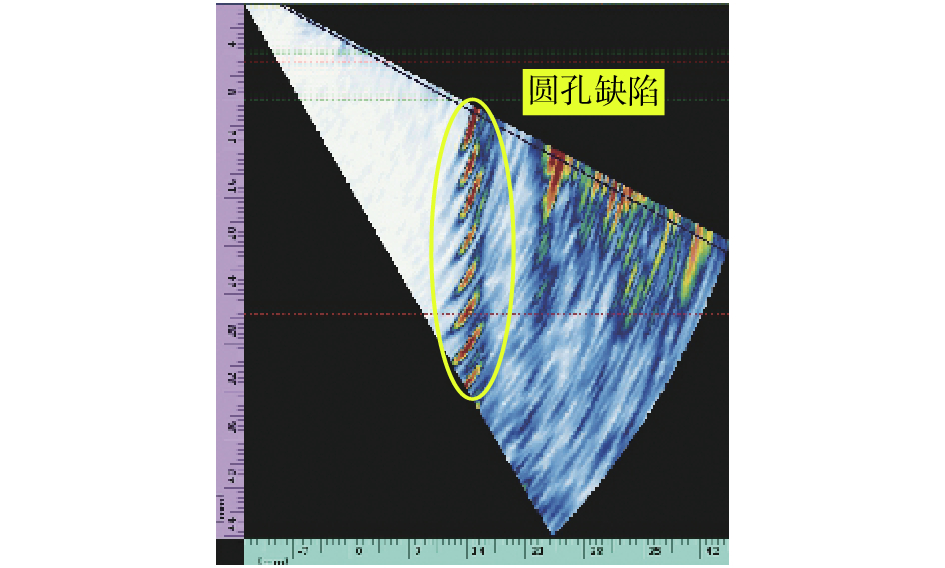
图8为时间增益补偿试验检测成像图,其横、纵坐标分别为水平方向检测距离(mm)、纵向检测深度(mm)。检测图像中纵向有效显示区红色像素越多表明超声回波幅值越大,即缺陷越大。由试验结果可看出,纵向分布的8个2 mm圆孔均被检出;根据红色像素点分布情况,对不同深度缺陷,超声时间增益控制模块能根据其所在位置进行相应补偿,达到精确检测缺陷大小的效果,验证基于CORDIC算法的超声时间增益补偿技术实际效果与价值。
|
| 图 8 时间增益补偿试验检测成像图 |
4 结束语
1) 本文基于超声相控阵回波信号时间增益控制技术原理及需求,提出采用扩展收敛域指数CORDIC算法对dB增益补偿曲线转换为实际放大倍数G(t)曲线的实时计算,再对超声回波采样信号进行数字补偿,降低时间增益控制模块硬件复杂度,提高时间增益控制精度,增大补偿范围。
2) 设计基于扩展收敛域的双曲系统指数CORDIC算法的dB-放大倍数对应求解器并进行精度测试,结果表明基于该算法计算超声回波实际增益最大相对误差不超过0.014%,精度满足超声相控阵时间增益控制需求。
3) 采用CORDIC算法dB-增益倍数求解器计算超声回波信号实际增益倍数,对不同深度处大小相同的缺陷进行补偿,仿真结果表明经过基于CORDIC算法的时间增益补偿后,不同深度处相同大小的缺陷回波强度保持一致,准确反映物体内部缺陷真实大小,提高超声相控阵检测准确性。
| [1] |
张宇, 王雪梅, 倪文波. 基于DDS和FPGA的数字式多脉冲激励超声检测系统设计[J].
中国测试, 2016, 42(06): 74-79.
|
| [2] |
陆铭慧, 胡梦雪, 孙霓, 等. 基于FPGA的超声相控阵接收系统的研究[J].
压电与声光, 2015, 37(5): 855-857.
DOI:10.11977/j.issn.1004-2474.2015.05.029 |
| [3] |
Volder J E. The CORDIC Trigonometric Computing Technique[J].
Electronic Computers Ire Transactions on, 1959, EC-8(3): 330-334.
DOI:10.1109/TEC.1959.5222693 |
| [4] |
Garrido M, Källström P, Kumm M, et al. CORDIC II: A New Improved CORDIC Algorithm[J].
IEEE Transactions on Circuits & Systems II Express Briefs, 2016, 63(2): 186-190.
|
| [5] |
陈旭文, 刘桂雄, 唐文明. 扩展收敛域任意对数CORDIC算法与FPGA实现[J].
中国测试, 2015(7): 108-111.
DOI:10.11857/j.issn.1674-5124.2015.07.025 |
| [6] |
唐文明, 刘桂雄. 指数函数CORDIC算法的FPGA定点化技术[J].
华南理工大学学报(自然科学版), 2016, 44(7): 9-14.
|
| [7] |
Aggarwal S, Meher P K, Khare K. Scale-Free Hyperbolic CORDIC Processor and Its Application to Waveform Generation[J].
IEEE Transactions on Circuits & Systems I Regular Papers, 2013, 60(2): 314-326.
|
| [8] |
牟胜梅, 李兆刚. 一种面向FPGA的指/对数函数求值算法[J].
计算机工程与应用, 2011, 47(33): 59-61.
DOI:10.3778/j.issn.1002-8331.2011.33.017 |
| [9] |
董世运, 李浩宇, 徐滨士, 等. HT250材料超声探伤中的衰减性探究[J].
中国测试, 2016, 42(3): 123-127.
DOI:10.11857/j.issn.1674-5124.2016.03.028 |
| [10] |
董志勇, 胡金榜. 超声波衰减系数法评估材料损伤的研究[J].
化工机械, 2007, 34(3): 139-143.
|
 2018, Vol. 44
2018, Vol. 44