文章信息
- 许艺青, 杨晓翔, 韦铁平, 姚进辉
- XU Yiqing, YANG Xiaoxiang, WEI Tieping, YAO Jinhui
- 基于正交试验的应变片敏感栅结构参数的优化
- Optimization of strain gauge structure parameters based on orthogonal test
- 中国测试, 2018, 44(6): 129-133
- CHINA MEASUREMENT & TEST, 2018, 44(6): 129-133
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018.06.024
-
文章历史
- 收稿日期: 2017-10-11
- 收到修改稿日期: 2017-12-29
2. 福州大学机械工程及自动化学院,福建 福州 350116;
3. 泉州师范学院, 福建 泉州 362000;
4. 福建工程学院机械与汽车工程系,福建 福州 350118;
5. 福建省计量科学研究院,福建 福州 350003
2. School of Mechanical Engineering and Automation, Fuzhou University, Fuzhou 350116, China;
3. Quanzhou Normal University, Quanzhou 362000, China;
4. School of Mechanical and Automotive Engineering, Fujian University of Technology, Fuzhou 350118, China;
5. Fujian Province Institute of Metrology, Fuzhou 350003, China
电阻应变片广泛应用于工程结构、应变测量及制造各种物理量传感器,特别是测力传感器、称重传感器和压力传感器等领域,因此,电阻应变片的测量结果的可靠性和准确性尤为重要[1]。Vadivuc-hezhian等[2]和Subrahmanya等[3]研究胶粘剂材料及其厚度对电阻应变片应变测量的影响,结果表明随着胶结层厚度的增加,应变损失增大。Komurlu等[4]将电阻应变片粘贴在混凝土上,对氰基丙烯酸酯、聚氨酯和环氧树脂胶粘剂进行试验对比,结果表明氰基丙烯酸酯在应变片测量结果中最准确。Zike等[5]建立基体和电阻应变片的三维模型,研究了弹性模量从1~200 GPa的基体材料对应变测量的影响,并进行修正。Zhou 等[6]提出了一种应变片布置优化的通用框架,并结合案例分析验证了框架的有效性,为结构性能评估的实际应用提供了方便。张佳明等[7]建立高温应变片参数高精度标定装置,确定影响高温应变片测量结果的参数,并进行补偿。王文瑞等[8-9]自主研制丝式高温应变片,建立简支梁、胶层、敏感栅有限元模型研究敏感栅结构参数对测量精度的影响,结果表明丝式敏感栅越细测量精度越高;高温应变片的敏感栅间距与长度具有精度最优值。胡玉梅等[10]建立含应变片的悬臂梁模型,分析了丝式应变片敏感栅不同的直径、栅长、栅丝间距对应变传递误差的影响,结果表明栅长、栅间距在基体应变传递中具有中间最优值,栅丝直径越小应变传递误差越小。尹福炎[11]利用有限元法研究了不同敏感栅的材料、厚度和端环长度等对应变片性能的影响。
由上可知,对电阻应变片的研究主要集中在粘贴工艺、胶粘剂材料、丝式应变片结构参数及温度对其性能的影响,对箔式电阻应变片敏感栅几何参数对应变传递的影响研究较少,而且大部分研究都是单一变量。为此,本文建立了等强度梁、基底和箔式敏感栅所组成的测量模型,采用正交试验对电阻应变片敏感栅材料、栅丝厚度、栅长和栅丝间距等因素进行了参数组合设计,利用ANSYS有限元软件进行分析,揭示这些因素对应变片性能和应变传递误差影响,找出最佳组合方案和不同参数的影响主次,为电阻应变片的结构设计和应变片的选择提供了依据。
1 电阻应变片工作原理电阻应变片的工作原理是基于金属的应变效应。应变片借助于各种胶粘剂粘贴于试件表面,当试件受力产生变形时,应变片敏感栅也随之发生变形,引起阻值发生相应的变化,再把这一电阻变化转换为电信号变化输出。
电阻应变片主要由基底、敏感栅、覆盖层及引线等组成,其结构如图1所示。基底和覆盖层由绝缘材料制成,起保护和固定敏感栅的作用。敏感栅是把应变量转换成电阻变化量的部分,常用的箔材有铜镍合金、镍铬合金、铁铬铝合金和铂铱合金等金属材料,其厚度一般取1~5 μm,栅长根据使用目的不同,有0.2 mm到几百毫米,栅丝间距由使用条件来选定,一般来说栅丝间距的大小是整数倍的单栅丝宽度。
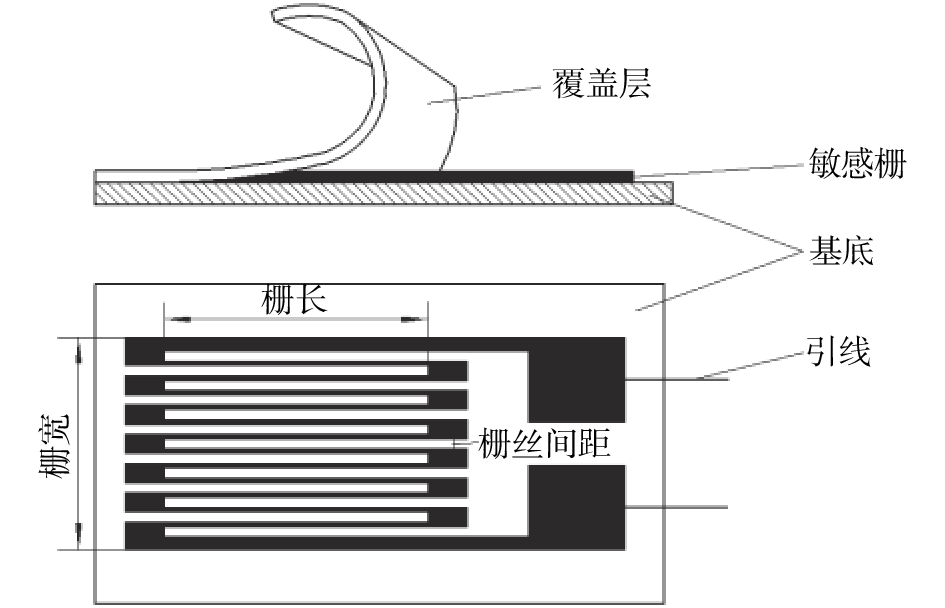
|
| 图 1 电阻应变片的典型结构 |
2 有限元模型建立和分析
为了解电阻应变片测量规律,取某型号120 Ω的电阻应变片,建立了含等强度梁、敏感栅和基底的三维简化模型,各部分的力学性能如表1所示。对等强度梁与应变片粘贴处进行网格加密划分,有限元网格模型如图2所示。各部分均采用八节点六面体实体单元solid185,模拟时将等强度梁左端全约束,在右端施加载荷50 kN。
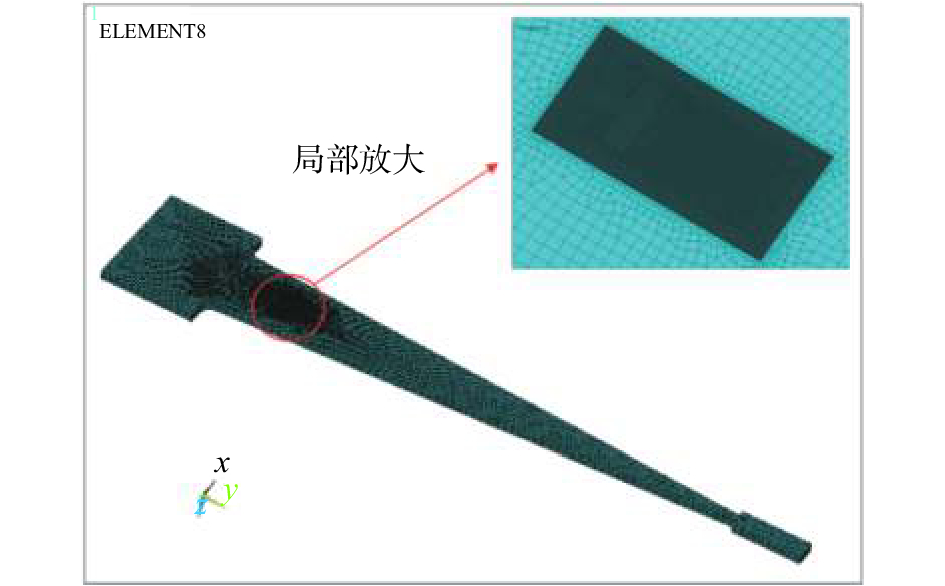
|
| 图 2 有限元网格模型 |
图3为等强度梁y向(沿梁的轴线方向)应变云图,可以看出,等强度梁最大应变8.08×10-4,发生在固定端处,提取等强度梁贴片位置中间20个节点的应变εs为6.90×10-4。
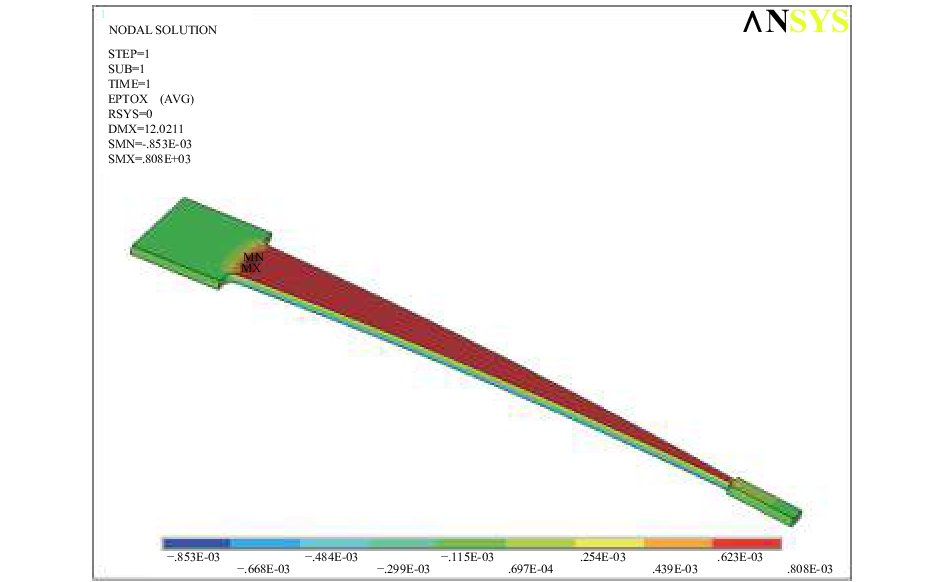
|
| 图 3 等强度梁y向应变云图 |
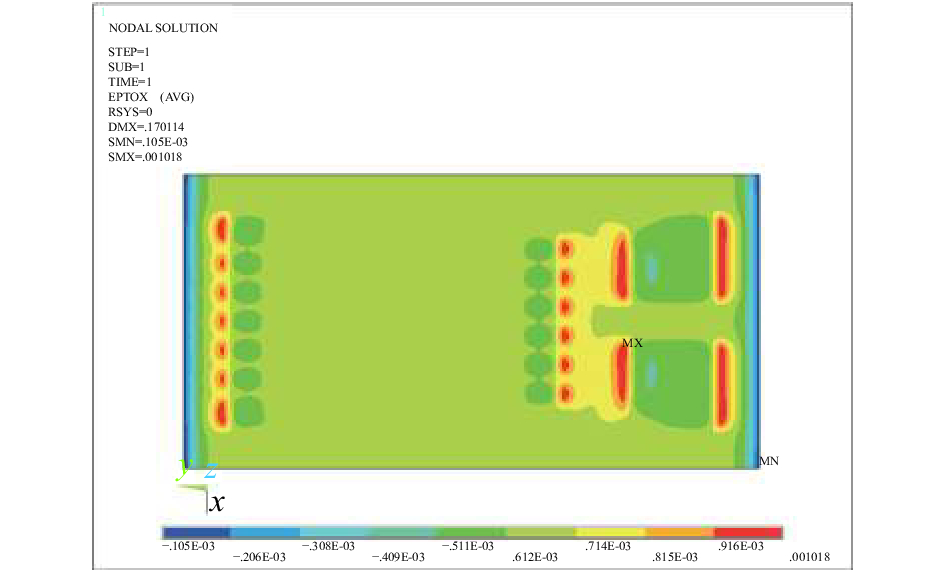
图4、图5分别为敏感栅和基底沿y方向(栅丝方向)应变云图,从图4可知,敏感栅所受最大应变为1.055×10-3,最小应变为5.05×10-4,每根栅丝中间受力较均匀,并向两端逐渐递减,两端所受的应变几乎为0。从图5可知,基底在与敏感栅边界交界处发生应变突变,所受最大应变为1.018×10-3,最小应变为0.105×10-3,基底两端应变几乎为0。取应变片敏感栅中间20个节点y向应变的平均值εh为6.84×10-4,作为应变片的测量值。
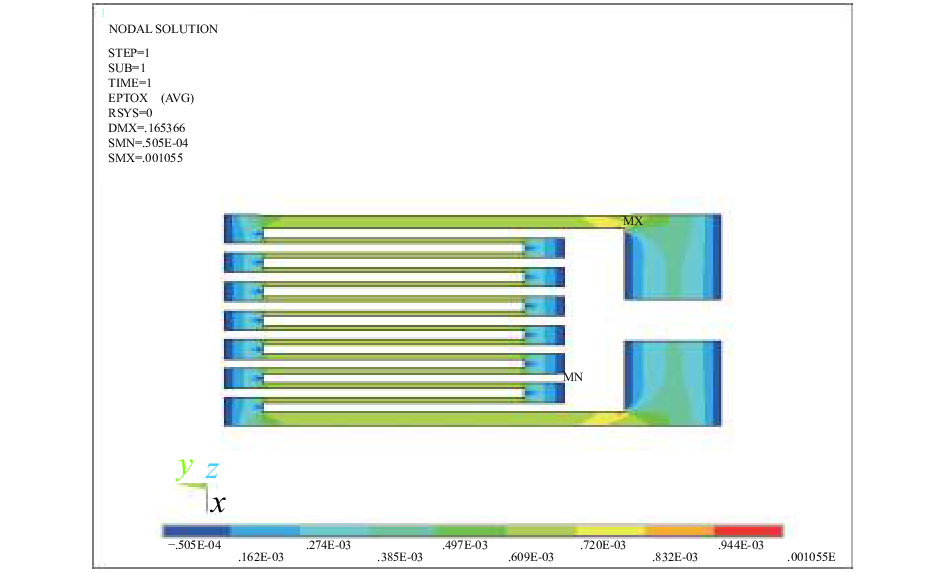
|
| 图 4 敏感栅沿y轴方向应变云图 |
|
| 图 5 基底沿y轴方向应变云图 |
由文献[13]可知,等强度梁与敏感栅的应变传递率为
| $\alpha = \left[ {1 - \frac{{\cosh \left( {kx} \right)}}{{\cosh (kL)}}} \right]$ | (1) |
式中:k—剪滞系数,
n—栅丝数目。
将各部分几何参数带入式(1)可得应变传递率的理论值,有限元应变传递率为敏感栅和等强度梁有限元应变值的比值。理论解与有限元解的对比如表2所示,理论解与有限元解应变传递率误差为0.8%,由于建模时对模型进行简化处理,故有限元结果与理论值存在一定误差,仿真结果与理论值计算基本一致。
| 等强度梁有限元应变值 | 敏感栅有限元应变值 | 理论应变传递率 | 有限元应变传递率 | 理论解与有限元解应变传递率误差 |
| 6.9×10-4 | 6.84×10-4 | 99.9% | 99.1% | 0.8% |
3 敏感栅结构参数对应变传递的影响 3.1 正交试验设计及结果
由工程经验可知,应变片的性能特性,不仅与所用的箔材材料、胶粘剂和制作工艺等有关,而且还与应变片敏感栅结构的几何形状密切相关。在设计箔式应变片时通常考虑敏感栅的材料、箔栅厚度、栅长和栅宽等。因此,本文基于有限元法,结合正交试验,综合分析以上参数对电阻应变片应变传递的影响。
选择如下4个影响因素:箔栅材料(A),栅丝厚度(B),栅长(C),栅丝间距(D)。每个因素取3个水平,如表3所示。
为便于描述,A的3个水平分别用A1、A2、A3表示,以此类推。
若全面试验则有81个水平组合,如A1B1C1D1,A1B1C1D2,A1B1C1D3等,全面试验要求的试验太多,因此采用正交试验,采用L9(34)正交表,按4因素3水平安排试验,从而选择最佳的敏感栅结构参数,试验模拟结果如表4所示。
| 试验号 | A | B | C | D | A | B | C | D | 有限元应变传递率误差/% |
| 弹性模量/GPa | 栅丝厚度/mm | 栅丝长度/mm | 栅丝间距/mm | ||||||
| 1 | 1 | 1 | 1 | 1 | 169 | 0.003 | 1 | 0.056 | 26.17 |
| 2 | 1 | 2 | 2 | 2 | 169 | 0.005 | 3 | 0.112 | 4.24 |
| 3 | 1 | 3 | 3 | 3 | 169 | 0.01 | 4 | 0.28 | 5.94 |
| 4 | 2 | 1 | 2 | 3 | 180 | 0.003 | 3 | 0.28 | 2.83 |
| 5 | 2 | 2 | 3 | 1 | 180 | 0.005 | 4 | 0.056 | 0.57 |
| 6 | 2 | 3 | 1 | 2 | 180 | 0.01 | 1 | 0.112 | 54.03 |
| 7 | 3 | 1 | 3 | 2 | 206 | 0.003 | 4 | 0.112 | 4.10 |
| 8 | 3 | 2 | 1 | 3 | 206 | 0.005 | 1 | 0.28 | 34.37 |
| 9 | 3 | 3 | 2 | 1 | 206 | 0.01 | 3 | 0.056 | 28.29 |
| T1/% | 36.35 | 33.10 | 114.57 | 55.02 | 160.54 | ||||
| T2/% | 57.43 | 39.18 | 35.36 | 62.38 | |||||
| T3/% | 66.76 | 88.26 | 10.61 | 43.14 | |||||
| M1/% | 12.12 | 11.03 | 38.19 | 18.34 | |||||
| M2/% | 19.14 | 13.06 | 11.79 | 20.79 | |||||
| M3/% | 22.25 | 29.42 | 3.54 | 14.38 | |||||
| R/% | 10.14 | 18.39 | 34.65 | 6.41 | |||||
| 注:1)Ti表示的是同一水平下3次实验的误差之和;Mi表示的是Ti在3次实验的误差平均值;R是3个误差平均值的极差。 | |||||||||
3.2 试验结果分析
9次试验模拟结果中以第5组的误差最小,达到0.57%,相应的水平组合为弹性模量180 GPa、栅丝厚度0.005 mm、栅丝长度4 mm、栅丝间距0.056 mm是当前最好的水平搭配。
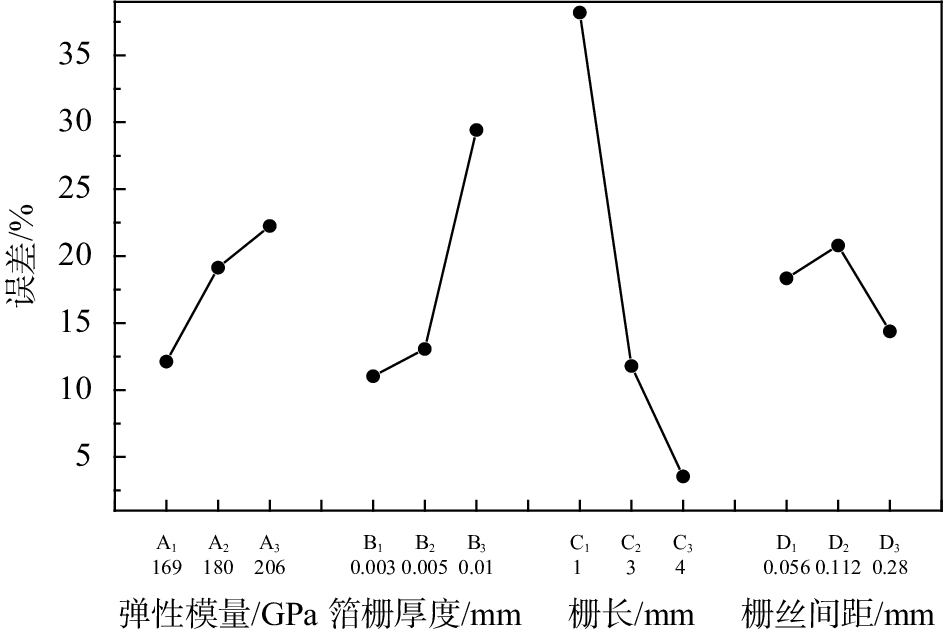
将4个因素的平均误差绘在同一张图上,如图6所示。可以看出,敏感栅的弹性模量越小,误差越小,以弹性模量169 GPa为最好;箔栅厚度越小,误差越小,以厚度0.003 mm为最好;栅丝长度越长,误差越小,以栅长4 mm为最佳。栅丝间距为0.28 mm时,误差最低。
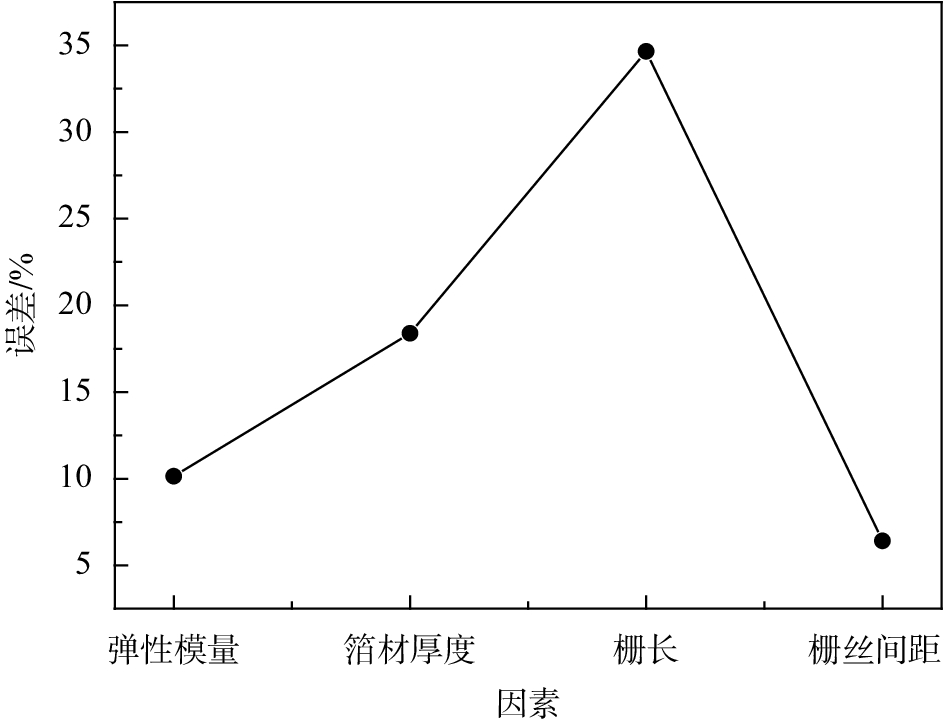
图7是4个因素和极差关系图。由图7可知各因素对结果影响大小的依次顺序是:C>B>A>D,即栅丝长度>栅丝厚度>弹性模量>栅丝间距。
|
| 图 6 应变传递平均误差与4个因素关系图 |
|
| 图 7 4个因素与极差关系图 |
通过上述分析,推断出最佳水平组合为A1B1C3D3,即弹性模量169 GPa,栅丝厚度0.003 mm,栅丝长度4 mm,栅丝间距0.28 mm。在9次正交试验中没有包含这个水平组合,因此要追加试验。通过有限元模拟分析,追加最佳水平组合试验的应变传递误差为0.19%,低于上述9次模拟的最好结果0.57%。
4 结束语采用正交试验对电阻应变片敏感栅结构参数进行了组合,探讨了其对于应变传递误差的影响,并讨论了各因素的影响主次。所建立的三维模型通过有限单元法模拟出的应变传递率为99.1%,该模型能正确反映应变片的应变传递。得出以下结论:
1)敏感栅的弹性模量和栅丝厚度越小,栅丝长度越长,误差越小,栅丝间距存在最优值。
2)4个因素对应变传递误差的影响主次的依次顺序是栅丝长度>栅丝厚度>弹性模量>栅丝间距。
3)通过实验分析得出最佳参数组合为弹性模量169 GPa,栅丝厚度0.003 mm,栅丝长度4 mm,栅丝间距0.28 mm,应变传递误差为0.19%。
| [1] |
SUBRAMANYA S B, PRASAD M G A. MEMS and MEMS based strain gauge load cells-A review[C]//Research & Technology in the Coming Decades. IET, 2014.
|
| [2] |
Vadivuchezhian K, Subrahmanya K, Chockappan N. Finite Element Modeling of Effect of Adhesive Layer and Carrier Thickness Used for Strain Gauge Mounting[J].
Advanced Materials Research, 2015, 1119: 828-832.
DOI:10.4028/www.scientific.net/AMR.1119 |
| [3] |
SUBRAHMANYA K, VADIVUCHEZHIAN K, CHOCKAPPAN N. Experimental Verification of Effect of Adhesive Layer Thickness Used for Strain Gauge Mounting[J].
Advanced Materials Research, 2015, 1119(3): 789-793.
|
| [4] |
Komurlu E, Cihangir F, Kesimal A, et al. Effect of Adhesive Type on the Measurement of Modulus of Elasticity Using Electrical Resistance Strain Gauges[J].
Arabian Journal for Science & Engineering, 2016, 41(2): 433-441.
|
| [5] |
Zike S, Mikkelsen L P. Correction of Gauge Factor for Strain Gauges Used in Polymer Composite Testing[J].
Experimental Mechanics, 2014, 54(3): 393-403.
DOI:10.1007/s11340-013-9813-7 |
| [6] |
Zhou K, Wu Z Y. Strain gauge placement optimization for structural performance assessment[J].
Engineering Structures, 2017, 141(15): 184-197.
|
| [7] |
张佳明, 王文瑞, 聂帅. 高温电阻应变片特性参数标定实验研究[J].
中国测试, 2014, 40(5): 25-28.
DOI:10.11857/j.issn.1674-5124.2014.05.006 |
| [8] |
王文瑞, 张佳明, 聂帅. 高温应变接触式测量精度影响因素研究[J].
固体火箭技术, 2015(3): 439-444.
|
| [9] |
王文瑞, 王刚, 胡挺,等. 高温应变栅丝蠕变对应变测量精度影响与补偿[J].
北京科技大学学报, 2017, 39(1): 88-95.
|
| [10] |
胡玉梅, 张方建, 邵毅敏,等. 应变片敏感栅结构参数对测量精度的影响[J].
重庆大学学报:自然科学版, 2013, 36(12): 21-27.
|
| [11] |
尹福炎. 箔式应变片结构模型与有限元分析[J].
衡器, 2009, 38(5): 47-50.
|
| [12] |
耿汉生. 应变胶性能与应变计的工作特性[J].
传感器用技术, 1990(4): 43-46.
|
| [13] |
王彪, 刘腾, 徐敬龙,等. 金属粘贴式电阻应变计应变传递分析[J].
中国测试, 2016, 42(8): 1-6.
DOI:10.11857/j.issn.1674-5124.2016.08.001 |
 2018, Vol. 44
2018, Vol. 44


