文章信息
- 苟轩, 王增增
- GOU Xuan, WANG Zengzeng
- 高频大电压阻容分压网络的频率特性研究
- Study on frequency characteristics of high frequency and large voltage resistor-voltage divider network
- 中国测试, 2018, 44(12): 152-156
- CHINA MEASUREMENT & TEST, 2018, 44(12): 152-156
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018.12.027
-
文章历史
- 收稿日期: 2018-08-15
- 收到修改稿日期: 2018-09-29
现代功率分析仪电压测量通道具有幅值范围大(1 000 Vrms)、频带宽(DC-10 MHz)、精度高的特点。主流的高精度功率分析仪电压测量精度:在DC-1 kHz优于0.1%,在1~100 kHz优于0.5%。针对这些特点,阻容分压网络是最理想的实现方式。制作良好的阻容分压网络具有测试频率范围大、幅值平坦度高、稳定性好等优点,测试的幅值可以高达几千伏,频率基本覆盖了试验电压的全部范围——从直流、工频到脉冲电压[1-6]。降低电压的常用方法是简单的电阻分压网络,这适合直流和低频应用,对于高于千赫兹的频率,必须考虑电阻和PCB(印刷电路板)的寄生行为,并进行必要的补偿[7]。澳大利亚国家测量研究院和瑞典国家测试研究院已经讨论过这个问题,并在其出版物中介绍了两个分压网络[8]。经过试验发现,高精度分压电阻结合校准容易保证低频段测量精度,中高频段1~100 kHz幅值平坦度受寄生参数影响非常大。阻容分压网络通常作为一种独立元件阻容分压器进行研究,但考虑到寄生参数对其频率特性的影响,需要进行复杂的阻容匹配以消除或减小寄生参数的影响[9],这种匹配方法不适合应用在功率分析仪中。本文建立阻容分压网络寄生参数模型,分析了各类寄生参数,并提出了一种工程上容易实现的寄生参数匹配方法;通过PSPICE仿真评估了寄生参数对分压网络频率特性的影响,并制作实物进行性能验证。
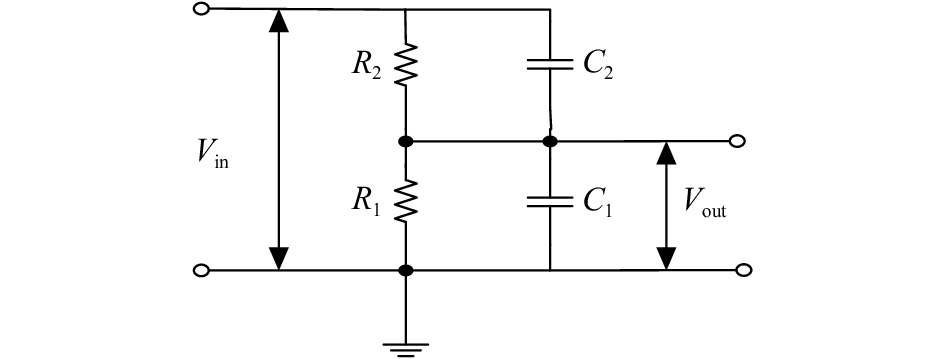
1 阻容分压网络模型 1.1 理想模型不考虑寄生参数,理想的阻容分压网络模型如图1所示。分压网络的分压比为
|
| 图 1 理想的阻容分压网络模型 |
| $\frac{V_{\rm out}}{V_{\rm in}} = \displaystyle\frac{{{R_1}}}{{{R_1} + {R_2} \cdot \displaystyle\frac{{1 + {\rm j}\omega {R_1}{C_1}}}{{1 + {\rm j}\omega {R_2}{C_2}}}}}$ | (1) |
无论在高频还是低频状态下,分压网络分压比均应维持恒定,从谐波的角度来讲,被测信号的各频率成分要以相同的变化传输,因此需满足:
| ${R_1}{C_1} = {R_2}C_2$ | (2) |
从式(2)看出,当满足R1C1=R2C2时,分压比与频率无关。因而,阻容分压网络具有良好的频率特性,工作频带宽,不易产生振荡[6]。
1.2 实际模型在高频时,寄生参数会对阻容分压网络的频率特性造成很大的影响,使用时,需要考虑以下2种寄生效应。
1)电阻寄生
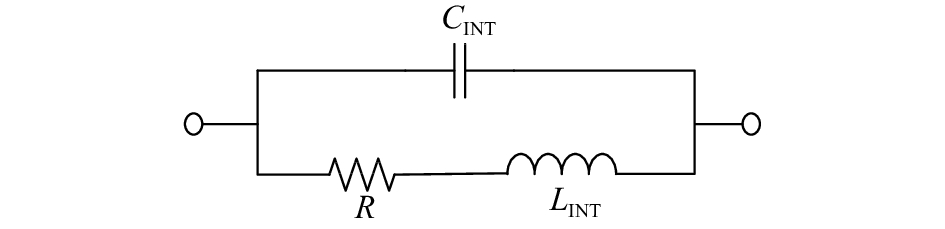
实际电阻都是非理想的,存在一定的极间电容和引线电感,实际电阻的等效模型如图2所示。R为标称电阻,LINT为引线电感,CINT为极间电容。
|
| 图 2 电阻等效模型 |
低频时,内部电感LINT的感抗几乎为零,内部电容CINT的容抗非常大,结果整个电路的阻抗几乎等于标称电阻;高频时,内部电感LINT开始增加电路的阻抗;内部并联电容CINT开始降低电路的阻抗。文献[10]中给出不同封装的表贴电阻的极间电容CINT的数值大约在37 fF~60 fF。
2)布局寄生
对于电子元件载体—电路板,必须考虑另外两个寄生电容:每个焊盘及焊盘之间的连线到信号地的杂散电容CGND和电阻两个焊盘之间的电容CPAD。杂散电容CGND可以像简单的平板电容器那样计算;焊盘电容CPAD取决于焊盘的几何形状和两个焊盘的间隙。
| $C = \frac{{\varepsilon S}}{{4\pi kd}}$ | (3) |
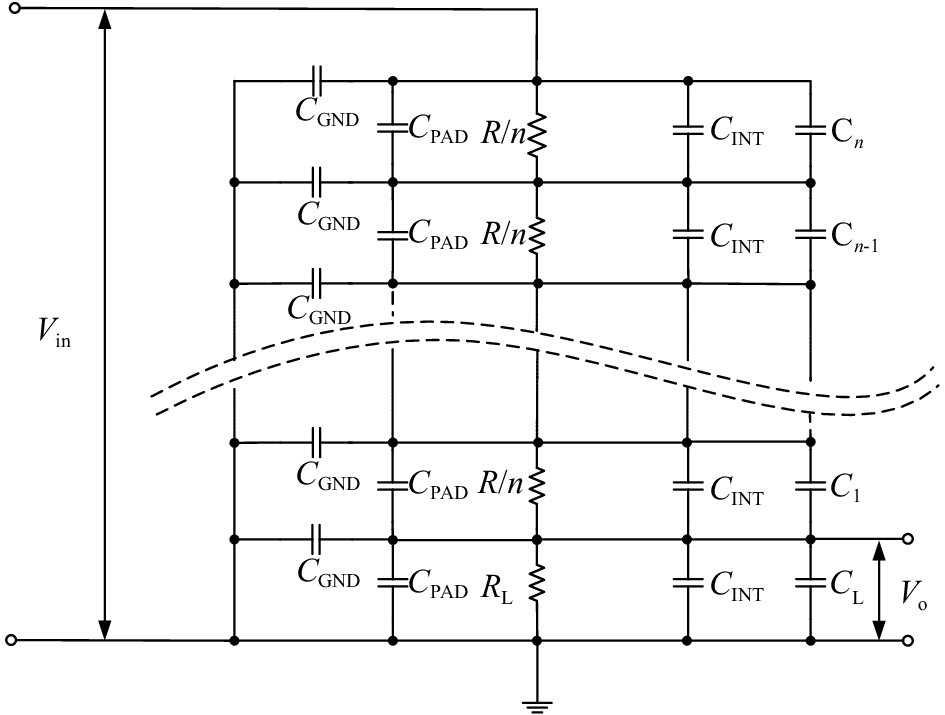
阻容分压网络的高压臂电阻通常由多个电阻串联而成,尤其是在高压测量时,因此引入了更多的寄生参数,这些寄生参数会对分压网络的频率特性造成很大影响。将寄生参数考虑进电路,分压网络的实际电路模型可以用图3表示。C1~Cn为使用2.1节匹配方法引入的补偿电容。CL为负载电容,包括补偿电容、后级电路输入电容和布线杂散电容等。
|
| 图 3 阻容分压网络模型及传统匹配方法 |
2 阻容匹配问题
对于大于数千欧姆的电阻器,内部并联电容将在高频处占主导地位[8],一般分压网络几乎都采用大于数万欧姆的电阻,尤其是在高压测量时。因此,进一步的研究将忽略内部电感LINT的影响。为了减小寄生电容CINT、CPAD和CGND对阻容分压网络频率响应的影响,需要在分压电阻旁并联一个更大的补偿电容。补偿电容放置的位置及取值都对分压网络频率特性有较大的影响,下面介绍两种匹配方法。
2.1 匹配方法1文献[9]中提出了一种分压网络的阻容匹配方法,如图3所示,每个高压臂电阻并联一个补偿电容C1~Cn,对整个分频器进行节点分析并给出了补偿电容Cp的精确解。Cp的作用是消杂散电容CGND对分压网络频率特性的影响,保证整个分压网络的分压比不受频率变化的影响。这里计算的Cp是并联在分压电阻上的总电容,已将CPAD和CINT等效在内,具体计算公式为:
| $Cp = \frac{{n{C_{\rm L}}{R_{\rm L}}}}{R} + \frac{{p(p - 1)}}{2} \cdot {C_{\rm GND}} + \frac{{n{R_{\rm L}}(p - 1)}}{R} \cdot {C_{\rm GND}}$ | (4) |
其中p=1,2,3,···,n;CGND为每个节点的对地杂散电容。R为高压臂电阻,n表示n个等值电阻串联;RL和CL分别为低压臂电阻和补偿电容。
以功率分析仪中阻容分压网络为例,R=1 800 kΩ,由9个200 kΩ电阻串联而成,RL=200 kΩ,据式(3)计算得CGND=0.15 pF,取CL=100 pF,带入式(4)计算出补偿电容Cp取值如表1所示。
| Cp | C1 | C2 | C3 | C4 | C5 |
| 容值 | 100 | 100.3 | 100.75 | 101.35 | 102.1 |
| Cp | C6 | C7 | C8 | C9 | |
| 容值 | 103 | 104.05 | 105.25 | 106.6 | |
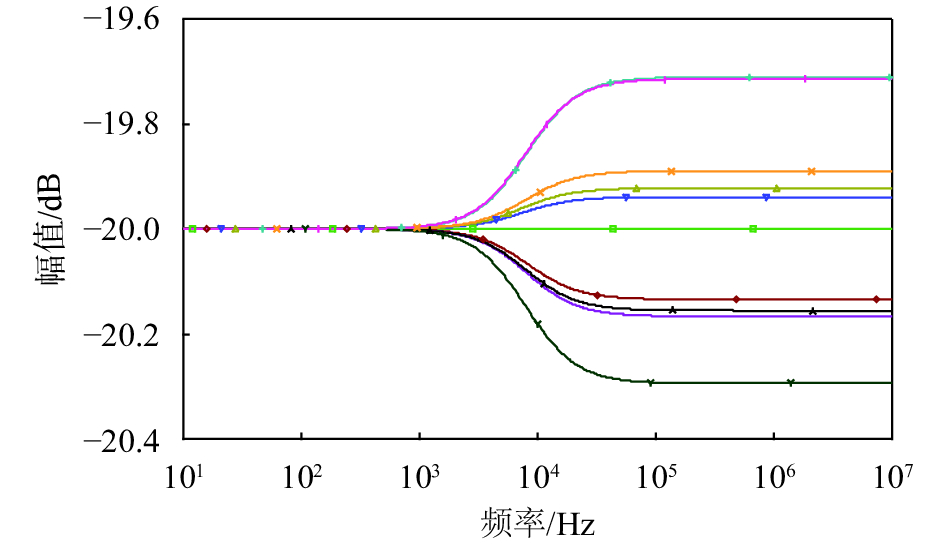
这里需要考虑的一个问题是电容本身存在较大的容值误差,标称值并不等于实际值,目前设计常用的贴片电容误差为±5%,实际应用时容值误差对分压网络的频率特性的影响不可忽略。利用PSPICE仿真验证电容误差对分压网络频率特性的影响,补偿电容Cp按照表1取值,设置误差为±5%,仿真结果如图4所示。中间最为平坦的一条是补偿电容Cp按照理论取值时的频率特性仿真曲线,其余9条是Cp在±5%误差范围内呈均匀分布且随机取值的仿真曲线。电容误差越大时,曲线在高频段偏离理论曲线越远。当仿真曲线数量取得足够多时,得出分压网络在中高频段的测量误差高达0.3 dB,即3.5%。表1中补偿电容Cp取值大都不是标准值,需要多个电容拼凑;过多的补偿电容个数增加了PCB的布局难度,还有可能引入更多的寄生参数;另外布线杂散电容和后级电路的输入电容对分压网络频率特性的影响也没有考虑。因此上述匹配方法在实际应用中的可操作性并不强。
|
| 图 4 Cp存在误差时分压网络频率响应曲线 |
2.2 改进型匹配方法2
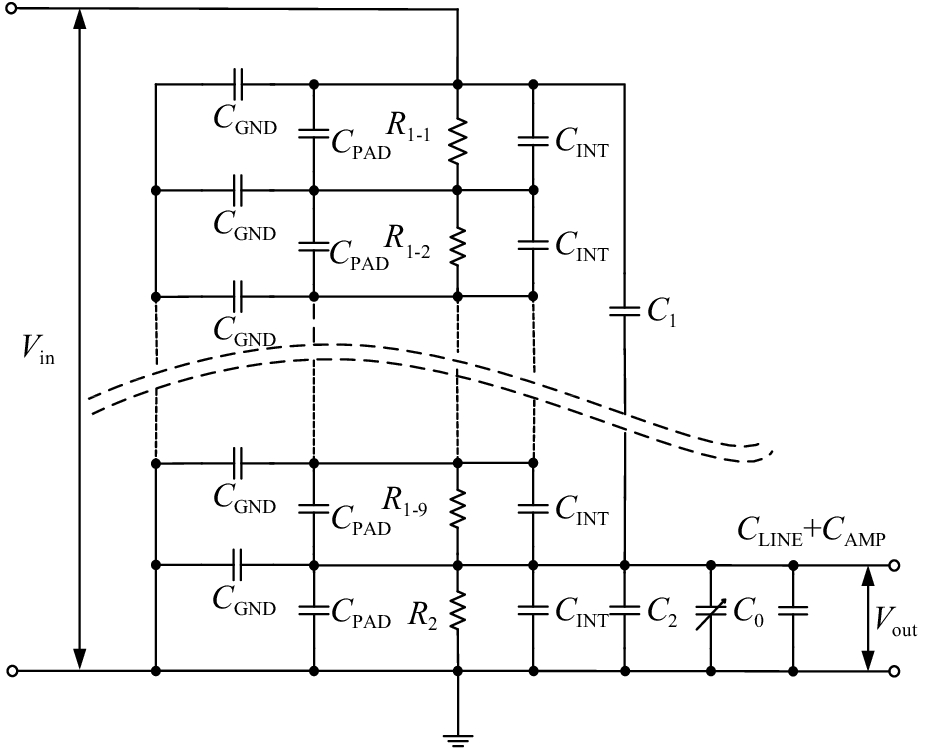
在功率分析仪研制过程中引入了新的分压网络匹配方法:高压臂电阻R1由9个等值电阻串联而成,在R1上只并联一个整体的补偿电容C1;在低压臂电阻R2上并联一个固定补偿电容C2和一个可调电容C0,通过调节C0可以消除电容容值误差、布线杂散电容和后级电路输入电容的影响。相较于匹配方法一,这种设计减少了匹配电容数量,利用可调电容误差C0解决了电容误差随机性、布局线杂散电容和后级电路输入电容对分压网络频率特性的影响,能够获得更好的匹配效果,实际应用电路如图5所示。CLINE表示布线杂散电容,CAMP表示后接运放的共模输入电容。
|
| 图 5 阻容分压网络模型及新型匹配方法 |
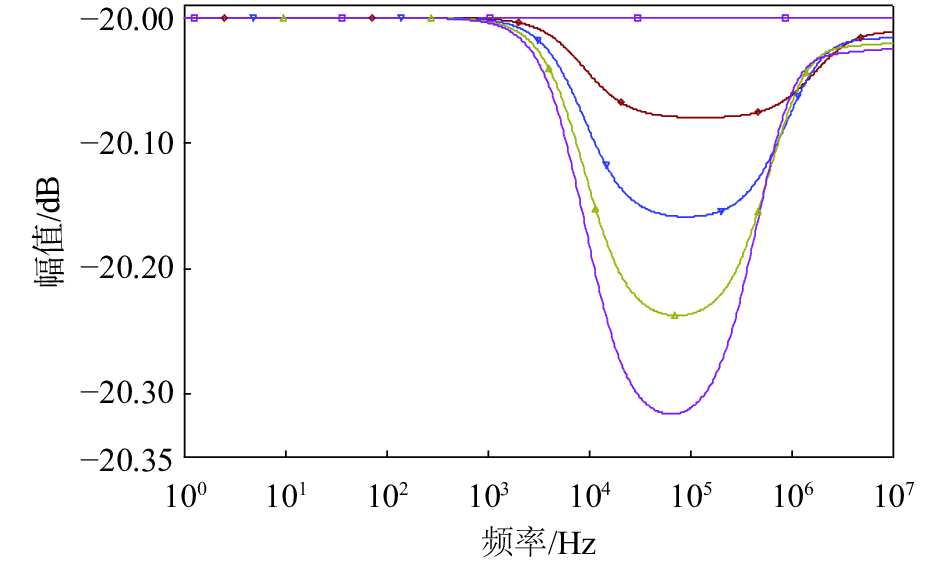
对于同一厂家,同一型号的表贴电阻,CINT基本相等;在同一块PCB上,都使用相同封装的贴片电阻,CPAD也近似相等。高压臂电阻R1由9个等值电阻串联而成,可以认为每个串联电阻上的寄生电容CINT和CPAD与其阻值已满足式(2),内部已经完成了匹配,所以CINT和CPAD对分压网络的性能影响甚小。图6的仿真结果验证了这一推论,最上面一条曲线设定CGND=0 pF,此时分压网络只受寄生参数CINT和CPAD的影响,其幅频特性曲线是一条完美的直线。
|
| 图 6 CGND不同时分压网络频率响应曲线 |
另外,图6中对地杂散电容CGND分别取值0 pF、0.05 pF、0.1 pF、0.15 pF、0.2 pF,对应的仿真曲线从上到下依次排列,发现在C1一定的条件下,CGND越小,分压网络的频率特性越好,因此分压网络的频率特性主要受对地杂散电容CGND大小的影响。R1上每个串联电阻的焊盘都存在一个对地杂散电容CGND,如果可以将CGND减小到可以忽略不计的地步,就能够很好地完成阻容匹配,提高分压网络的频率特性。根据图5,忽略CGND的大小,有:
| $\begin{split}&\frac{V_{\rm out}}{V_{\rm in}} \approx\\ &\frac{{{R_2}}}{{{R_2}\! +\! {R_1} \cdot \displaystyle\frac{{1 \!+\!{\rm j}\omega {R_2}({C_0} \!+ \!{C_2} \!+\! {C_{\rm LINE}} \!+ \!{C_{\rm AMP}} \!+\! {C_{\rm INT}} \!+\! {C_{\rm PAD}})}}{{1 + {\rm j}\omega {R_1}({C_1} + {C_{\rm INT}}/9 + {C_{\rm PAD}}/9)}}}}\end{split}$ | (5) |
若要保证分压比Vout/Vin不随频率变化而变化,首先需满足:
| $\frac{{{R_1}}}{{{R_2}}} \approx \frac{{{C_0} + {C_2} + {C_{\rm LINE}} + {C_{\rm AMP}} + {C_{\rm INT}} + {C_{\rm PAD}}}}{{{C_1} + {C_{\rm INT}}/9 + {C_{\rm PAD}}/9}}$ | (6) |
对于前述的第2种匹配方法,通过仿真与实测发现,阻容分压网络的误差具有局部极值。究其原因,低频时,分压网络容抗大阻抗小,信号主要流经分压网络的电阻支路;高频时,分压网络阻抗大容抗小,信号主要流经分压网络的电容支路;而在中间某段频率时,阻抗容抗大小相当,信号基本均等的流过两个支路,但是受杂散电容影响,阻容没有得到良好的匹配,此时分压网络就出现了误差。
3.1 影响因素分压网络频率特性误差极值发生的频率ƒ与R1、C1有关系,极值|D(f)|主要受补偿电容C1和对地杂散电容CGND的影响,可以近似得到:
| $f \approx \frac{1}{{{R_1}{C_1}}}$ | (7) |
| $\left| {D\left( f \right)} \right| \propto \frac{{{C_{\rm GND}}}}{{{C_1}}}$ | (8) |
为了尽可能减少误差极值的影响,可以选择较小的R1和较大的C1[11],但这样降低了分压网络的输入阻抗;作为测试仪器,应该是R1越大和C1越小越好,以减小仪器输入级对被测电路的影响;另外受限于电容C1耐压值与容值之间的矛盾,C1也不可能太大。前文已经讨论过,CINT和CPAD对分压网络的性能影响甚小,实际应用中,在满足式(6)的条件下,应尽力减小CGND的大小。
3.2 实物验证在功率分析仪中,分压网络的输入信号幅值最大为1 000 Vrms,同时还需满足高带宽和高精度的需求。在满足电阻耐压和功率的前提下,分压电阻的寄生参数LINT、CINT、CPAD和CGND应尽可能小[12],设计中选用了1206封装的高精度表贴电阻;另外,补偿电容要求稳定性好、温漂低、高频特性好,尤其是高压臂的补偿电容承受将近1 000 Vrms电压,选用的是C0G介质高压陶瓷电容。
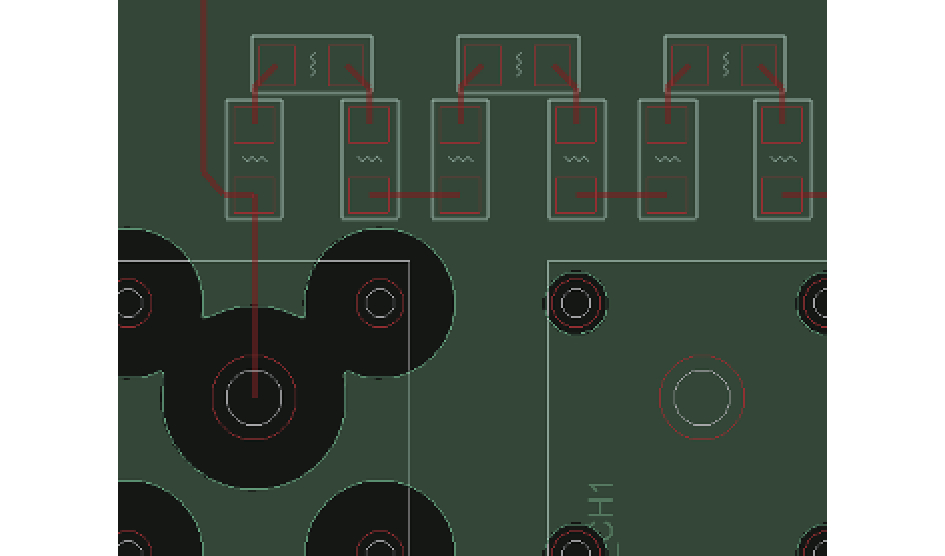
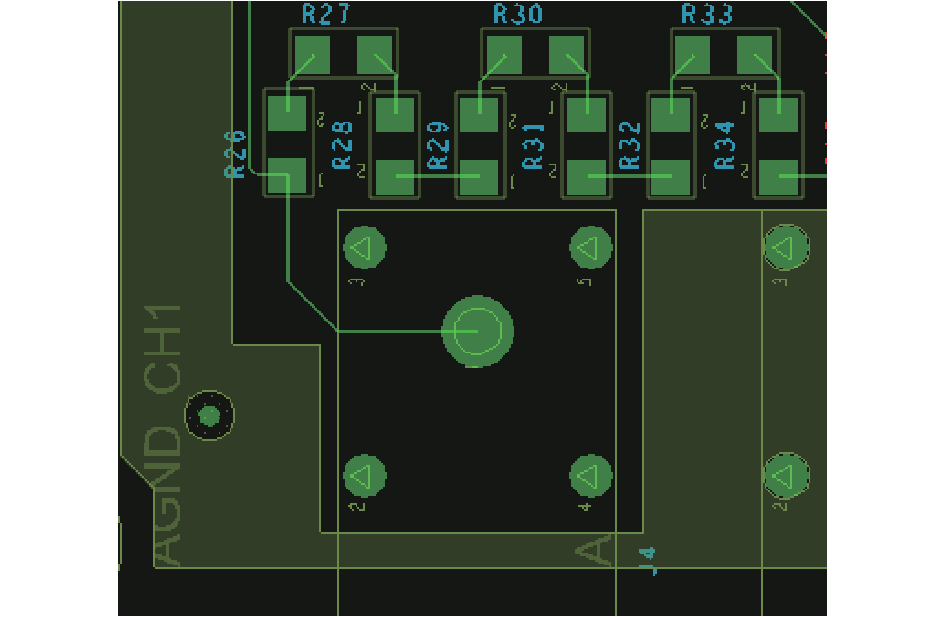
为了验证CGND对阻容分压网络频率特性的影响,设计了两种PCB布局,图7和图8分别是在阻容分压网络下方铺设和不铺设接地层。
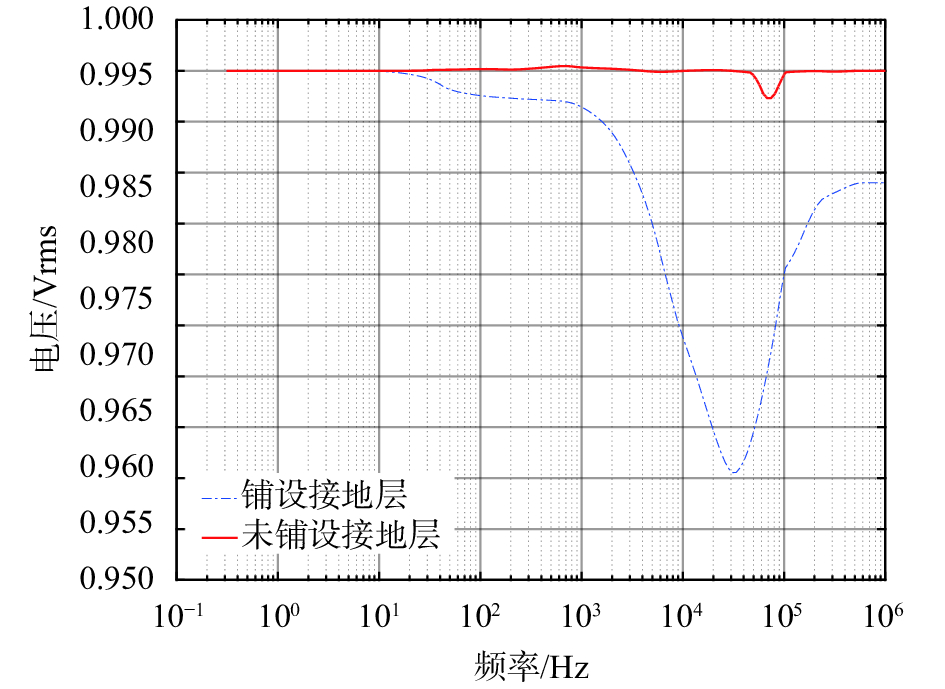
针对图7和图8中的两种电路布线,在室温下,通过FLUKE电压校准仪为分压网络提供输入信号,使用功率分析仪的测量功能记录1 MHz内各个频点的实际测量电压值,利用Matlab绘制出如图9所示的实测对比曲线。分压网络下方铺设接地层时,每个焊盘及焊盘之间的走线对地都有杂散电容,此时CGND较大,电压测量通道带内不平坦度最大可达4%,测量误差主要集中在1 ~100 kHz频带范围内;分压网络下方不铺设接地层时,对地杂散电容CGND较小但仍然存在,电压测量通道带内不平坦度小于0.3%,测量误差的频带范围也变得很窄,能满足高精度功率分析仪小于0.5%的设计需求。针对这两种PCB布局,图9中实测曲线验证了在C1一定的条件下,CGND越小,分压网络的频率特性越好。且随着CGND增大,测量误差极值点频率越低。这与图6中的幅频特性仿真结果近似,验证了寄生参数模型构建的准确性。实物测试中CGND容值无法准确测出,对比图6和图9,可反推出实物测试中CGND大于0.2 pF。说明阻容分压网络下方不铺设接地层是降低寄生参数CGND一种行之有效的工程实现方法,对提高整个分压网络的幅频响应具有重要意义。
|
| 图 9 铺设接地层和未铺设接地层实测数据曲线 |
|
| 图 7 分压网络下方铺设接地层 |
|
| 图 8 分压网络下方不铺设接地层 |
4 结束语
高压测量中阻容分压网络的频率响应主要受高压臂电阻R1和补偿电容C1以及对地杂散电容CGND的影响。为了提高阻容分压网络的频率特性,首先要保证所选电阻电容的稳定性好、温漂低,并合理选用电阻电容值,做好阻容匹配;其次要尽可能减小对地杂散电容CGND的大小,以提高信号带内平坦度。
本文讨论的功率分析仪阻容分压网络,实现简单,具有良好的工程实践意义,适合应用在任何高频大电压测量场合。实测发现,在DC-1 MHz频带内,分压网络测量误差<0.5%,能满足高精度电压测量需求。
| [1] |
薛晔. 阻容分压网络的误差分析一例[J].
高压电器, 1998(1): 58-60.
|
| [2] |
吕亮, 王颂, 周会高, 等. 一种宽频带通用阻容混联式分压器的特性[J].
高电压技术, 2007, 4(14): 54-56, 113.
DOI:10.3969/j.issn.1003-6520.2007.04.014 |
| [3] |
朱金龙, 张大伟, 李政. 串联阻容分压网络频率特性仿真[J].
机电信息, 2015(27): 53, 55.
|
| [4] |
许灵洁, 周永佳, 周琦. 常用高压阻容分压器频率特性的研究[J].
浙江电力, 2011, 30(7): 13-15.
DOI:10.3969/j.issn.1007-1881.2011.07.004 |
| [5] |
赵东阳, 王剑飞, 李成祥, 等. 阻容串联分压器的设计与研制[C]// 重庆市电机工程学会2008年学术会议, 2008.
|
| [6] |
张龙, 魏光辉, 刘存礼. 10 kV脉冲标准分压网络的设计与研究[J].
宇航计测技术, 2008, 2(15): 54-56, 65.
DOI:10.3969/j.issn.1000-7202.2008.02.015 |
| [7] |
胡晓倩, 杨菁, 张莲. 电阻分压器的集中参数电路模型及分析[J].
重庆工学院学报(自然科学版), 2008, 7(24): 96-98, 116.
DOI:10.3969/j.issn.1674-8425-B.2008.07.024 |
| [8] |
GRUBMULLER M, SCHWEIGHOFER B, WEGLEITER H. Characterization of a resistive voltage divider design for wideband power measurement[C]// Sensors. IEEE, 2014: 1332-1335.
|
| [9] |
HEATON A G. Exact solution for capacitive compensation of the RC potential divider with lumped stray capacitances to earth[J].
Electronics Letters, 1969, 5(13): 279-280.
DOI:10.1049/el:19690212 |
| [10] |
ROBERT S J, CHARLES W, WILLIAM C, et al. Frequency response of thin film chip resistors[C]// CARTS USA 2005. Vishay Thin Film 2160 Liberty Drive Niagara Falls, 2005: 136-141.
|
| [11] |
张宣妮, 刘珍, 鲁帆. 电阻分压网络的电感补偿[J].
中国新技术新产品, 2008(15): 86-87.
|
| [12] |
POGLIANO U, TRINCHERA B, LANZILLOTTI M, et al. Characterization of resistive dividers for a wideband power analyzer[C]// Precision Electromagnetic Measurements. IEEE, 2014: 130-131.
|
 2018, Vol. 44
2018, Vol. 44


