文章信息
- 周晓平, 周伟, 郝江涛
- ZHOU Xiaoping, ZHOU Wei, HAO Jiangtao
- 基于TraPPE-UA势能模型的超高压乙醇分子动力学模拟
- Molecular dynamics simulation of ethanol under ultrahigh pressure based on TraPPE-UA potential energy model
- 中国测试, 2018, 44(1): 44-48, 100
- China Measurement & Test, 2018, 44(1): 44-48, 100
- http://dx.doi.org/10.11857/j.issn.1674-5124.2018.01.009
分子动力学模拟是依靠牛顿力学来模拟分子体系运动的一套分子模拟方法,不仅可以用于模拟物质的宏观性质,还可以得出微观结构、粒子运动等信息[1]。一般认为压强超过100 MPa就是超高压,物质在高压作用下,其物理和化学性质会发生巨大的变化,在超高压作用下,液体的压缩性显著增大[2-3]。高压物理实验面临着实验条件、费用、实验设备的限制,而分子动力学计算利用计算机模拟,可以很好地解决这些问题。乙醇分子是常见的有机、极性分子,常用于化工生产中,研究其热力学性质和动力学性质对工业生产有重要意义。且乙醇和水在很多性质上都存在相似性,被认为是水的理想替代物[4],关于乙醇性质的研究也一直是热点。张阳[5]用Monte Carlo方法研究了超临界乙醇的结构性质和氢键,压强范围从常压到高压70 MPa;Saiz等[6]用分子动力学方法模拟研究了不同热力学状态下液态乙醇的结构、氢键和扩散等动态性质;Markus等[7]研究了温度和压强(0.1~35 MPa)对甲醇和乙醇体系中氢键的影响。目前对乙醇的研究压强一般都在100 MPa以内,更高压强下乙醇性质的文章还少见报道。因此本文对液态乙醇的研究进行了补充,采用平衡分子动力学方法,模拟温度298~500 K、压强从10 MPa到超高压300 MPa条件下不同状态点乙醇的热力学性质、结构性质和动力学性质。本文的乙醇分子动力学模拟值可为其传质性质应用提供理论参考。
1 模型建立 1.1 势能模型势能模型的选取对模拟结果的准确与否有着决定性影响。目前文献中分子模拟常用的乙醇模型主要是全原子模型和联合原子模型。鉴于全原子模型所需的计算时间较长,因此大部分文献采用联合原子模型进行模拟。联合原子模型有OPLS-UA(optimized potentials for liquid simulations-united atom)模型和TraPPE-UA(transferable potentials for phase equilibria-united atom)模型两种。OPLS-UA模型由Jorgensen[8]开发,主要针对液相有机小分子,能够很好地模拟液态乙醇的各种动态性质。但是,在Chalaris和Samios[9-10]用OPLS-UA模型对超临界甲醇进行分子动力学模拟的研究中,压强模拟值的准确性很差,说明OPLS-UA势能模型在压强较高时并不能真实反映分子的动态性质。TraPPE-UA模型是由Siepmann[11]小组开发,由于其模型参数已经用实验的相平衡数据优化过,因此在很大的压强范围内都有较好的准确度。本文采用TraPPE-UA势能模型对高压下乙醇分子团簇的性质进行研究。
在TraPPE-UA模型中,乙醇分子由CH3、CH2基团和O原子、H原子合计4个作用位点构成。乙醇分子间的势能计算式为
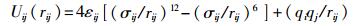 |
(1) |
式中:qi、qj——第i、j个原子或基团上所带电荷;
rij——原子或离子i与j间的距离;
σij、εij——原子间L-J作用参数。
 |
(2) |
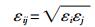 |
(3) |
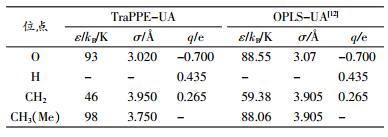
式(1)右侧第1项表示短程Lennard-Jones(L-J)势,第2项表示长程库仑势。TraPPE-UA模型和OPLS-UA模型的相关参数见表 1。
1.2 实验方法
本研究采用Materials Explorer软件,在温度为298,400,500 K,压强分别为10,100,300 MPa条件下对乙醇分子体系进行了分子动力学模拟。采用Nose-Hoover热浴法控制温度,完成不同压强条件下的等温模拟[13]。分子动力学模拟需进行以下假设:1)两体有效势能近似;2)最小镜像准则[14]。分子动力学模拟的起始构型为面心立方晶格,将乙醇分子的起始取向定为随机分布,采用立方周期性边界条件。模拟过程中所用的乙醇分子总数为100个。采用球形截去法进行位能截断[14],采用Ewald加和法求解长程静电相互作用力[15],采用Shake算法固定乙醇分子的几何构型[16]。分子动力学模拟过程中,每个分子都可视为是刚性体,运用五阶Gear预测-校正法求解体系的运动方程[17]。分子动力学模拟过程中,时间步长取10-15 s,单次模拟总时间取3×10-10 s,采用NVT系综进行10-10 s的初始化,使得体系达到相对平衡,随后在NPT系综中完成2×10-10 s的模拟,完成各种参数的计算,模拟过程中每隔10-14 s就输出一次构型,用于结果分析。
2 结果与分析 2.1 热力学性质焓是物质重要的热力学状态量,体系焓计算式为
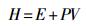 |
(4) |
式中:E——体系的内能,kJ;
P——体系的压强,MPa;
V——体系的体积,m3。
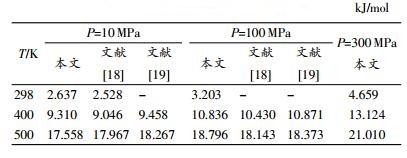
表 2是本文模拟温度为298,400,500 K,压强为10,100,300 MPa时乙醇的焓值,并与文献[18]的模拟值和文献[19]用状态方程推导的焓值进行比较,结果较为接近,可见本文模拟结果可靠。
从表中可以看出,当压强相同时,随着温度的升高乙醇体系的焓值逐渐增大。这是由于当温度升高,乙醇分子间的热运动加剧,体系内能增大,焓也跟着增大。相同温度下,本文模拟的焓值随压强的增大而增大,但文献[18-19]中焓随压强的变化关系不明确,由于现有文献中尚未见到高压下乙醇焓值实验数据的相关报道,此计算结果有待进一步验证。
2.2 结构性质径向分布函数(RDF)是反映物质微观结构的重要物理量,主要用于描述距离中心粒子为r处出现另一粒子的概率密度与随机分布概率密度的比值[13],其计算式为
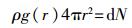 |
(5) |
式中:ρ——系统密度;
dN——距离中心分子(r,r+dr)区间内的分子数目。
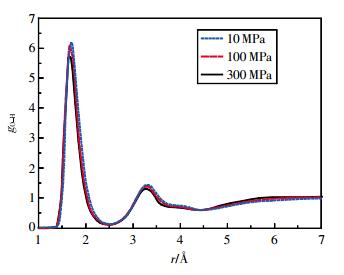
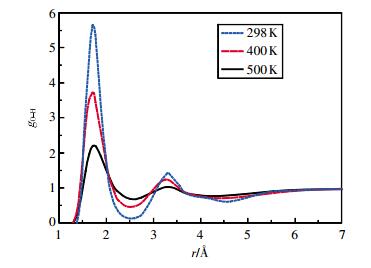
图 1为T=298 K时乙醇分子的氧氢径向分布函数随压强的变化。图 2为P=10 MPa时氧氢径向分布函数随温度的变化。
|
| 图 1 298 K时乙醇的氧氢径向分布函数 |
|
| 图 2 10 MPa时乙醇的氧氢径向分布函数 |
从图 1可看出,压强变化对OH径向分布函数第1峰影响较大,随着压强的增大,OH径向分布函数第1峰分别出现在1.69,1.67,1.65Ǻ,峰位逐渐左移,峰值依次减小,第2峰也下降,但不如第1峰明显,在Petravic[20]和Dellis[21]等的研究中,也发现了OH径向分布函数的第1峰随压强增大而减小的现象。计算结果表明,随着压强的增加,第一配位圈内乙醇分子间的氢原子与氧原子间距逐渐减小,氢键作用逐渐增强。
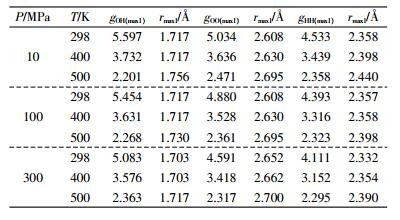
从图 2可看出,当压强相同时,随着温度的升高,OH径向分布函数第1峰和第2峰逐渐下降,峰谷抬高,峰位右移。计算结果表明随着温度的升高,乙醇分子间的氢原子与氧原子间距逐渐增大,氢键作用逐渐减弱。表 3为各状态点乙醇的OH、OO、HH径向分布函数第1特征峰值与峰位。随着温度的升高和压强的增大,OH、OO、HH径向分布函数第1峰峰值均下降,但OH径向分布函数的变化较OO、HH径向分布函数更为明显。
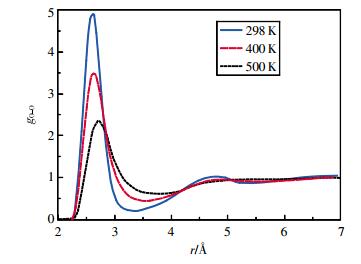
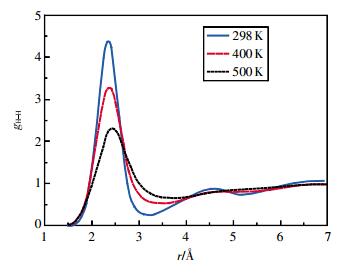
图 3、图 4为100 MPa时OO、HH径向分布函数随温度的变化。从图中可看出,相同压强下,随着温度的升高,OO、HH径向分布函数第1峰下降,峰位右移,峰谷抬高,第2峰也下降,且在500 K时,第2峰消失。这说明随着温度的升高,乙醇的长程有序程度逐渐下降。这与高压下水的结构随温度和压强变化的趋势相同[22]。
|
| 图 3 100 MPa时乙醇的氧氧径向分布函数 |
|
| 图 4 100 MPa时乙醇的氢氢径向分布函数 |
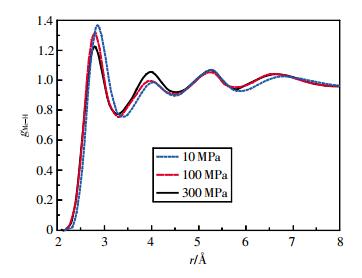
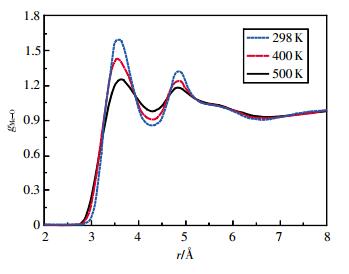
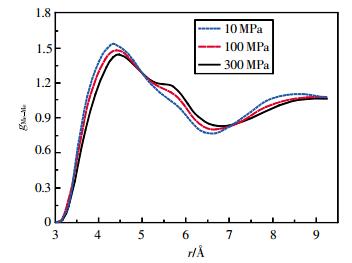
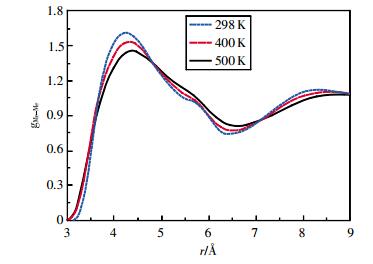
图 5~图 8为乙醇的MeH、MeO、MeMe径向分布函数。随着温度的升高和压强的增大,各径向分布函数第1峰变化最明显,峰高下降,峰谷抬高。500 K时,MeH径向分布函数的第2、3、4峰峰高已超过第1峰。MeMe径向分布函数第2峰逐渐消失。
|
| 图 5 298 K时乙醇的甲基氢径向分布函数 |
|
| 图 6 100 MPa时乙醇的甲基氧径向分布函数 |
|
| 图 7 400 K时乙醇的甲基甲基径向分布函数 |
|
| 图 8 300 MPa时乙醇的甲基甲基径向分布函数 |
通过对比不同原子和基团间径向分布函数的第一波谷位置rmin1可发现,rOH<rHH<rOO<rMeH<rMeO<rMeMe。计算结果表明:相同温度和压强下,第一配位圈内亲水的O原子与H原子距离最小,而疏水的烷基之间的距离最远。
2.3 动力学性质结合国内外研究现状,自扩散系数D的计算方法主要包括Einstein法和Green-Kubo法。Eintein法通过对均方位移(MSD)求斜率得到扩散系数。鉴于分子动力系统中的原子在永不停息地做无规则运动,各原子在不同时刻的位置都不相同。将

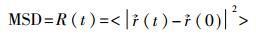 |
(6) |
式中 < >表示平均值。
根据统计学原理,只要分子数目足够多,计算时间足够长,系统的任一瞬间都可以当作时间的零点,所计算的平均值应该相同。根据爱因斯坦的扩散定律,扩散系数(diffusion constant)与均方位移的关系是:
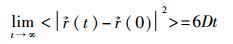 |
(7) |
式中D即为粒子的扩散系数。
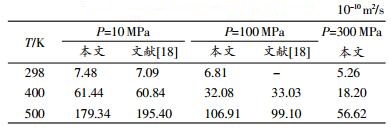
当模拟的时间很长时,均方位移对时间曲线的斜率的1/6就是扩散系数。表 4是本文用均方位移计算的乙醇的自扩散系数。
由表可知,在相同压强下,随温度的升高,乙醇的自扩散系数增大。这与文献[23]测定的常压下乙醇自扩散系数随温度的变化趋势相同,且随着压强的增大,这种变化趋势逐渐减缓。而相同温度下,随着压强的增加,乙醇自扩散系数逐渐减小。这是因为压强增大使乙醇分子之间的距离变小,分子间排列更为紧密,相互碰撞现象明显增加,从而阻碍了分子的扩散运动;当温度不断上升时,乙醇分子间的距离逐渐增加,相互作用力减弱,此时将有利于分子的扩散运动。本文模拟值与文献[18]的模拟结果基本一致,但在500 K,10 MPa时相差较大,由于实验条件的限制,高压下乙醇分子团簇的自扩散系数实验数据匮乏,有待进一步验证。
3 结束语本文模拟了温度298~500 K,压强从高压10 MPa到超高压300 MPa条件下乙醇分子体系的热力学性质、结构性质和动力学性质,并得出以下结论:
1) 相同压强下,乙醇体系的焓值随温度的升高而增大,本文模拟值与文献模拟值接近,本文所用TraPPE-UA模型可靠。
2) 通过对径向分布函数的研究,发现在压强很大的情况下,乙醇体系的结构依然很有规律。随着压强和温度的升高,各径向分布函数的第1峰高度明显下降,乙醇的长程有序程度下降。
3) 当压强相同时,乙醇的自扩散系数随温度的升高而增大,但压强增大时,这种变化趋势逐渐减缓。乙醇的自扩散系数随温度的升高而增大,而压强对扩散系数的影响与温度正好相反。
| [1] |
RAHMAN A. Correlations in the motion of atoms in liquid argon[J].
Phys Rev, 1964(136): 405-411.
|
| [2] |
曾勇平, 朱晓敏, 杨正华. 水、甲醇和乙醇液体微结构性质的Car-Parrinello分子动力学模拟[J].
物理化学学报, 2011, 27(12): 2779-2785.
DOI:10.3866/PKU.WHXB20112779 |
| [3] |
曾勇平, 时荣, 杨正华. Be~(2+)在水、甲醇和乙醇中结构性质的从头算分子动力学模拟[J].
物理化学学报, 2013, 2(10): 2180-2186.
DOI:10.3866/PKU.WHXB201307152 |
| [4] |
罗辉, 王睿, 范维玉, 等. 分子动力学模拟计算超临界CO的溶解度参数[J].
石油学报(石油加工), 2015, 31(1): 78-83.
|
| [5] |
张阳. 分子模拟在纯超临界流体及其二元混合物体系中的应用[D]. 北京: 清华大学, 2005.
http://cdmd.cnki.com.cn/Article/CDMD-10003-2006067189.htm
|
| [6] |
SAIZ L, PADRO J A, GUARDIA E. Structure and dyna mics of liquid ethanol[J].
Phys Chem B, 1997(101): 78-86.
|
| [7] |
MARKUS M, HOFFMANN, MARK S C. Are there hydrogen bonds in supercritical methanol and ethanol[J].
Phys Chem B, 1998(102): 263-271.
|
| [8] |
JORGENSEN W L. Optimized intermolecular potential functions for liquid alcohols[J].
Phys Chem, 1986(90): 1276-1284.
|
| [9] |
CHALARIS M, SAMIOS J. Hydrogen bonding in supe-rcritical methanol A molecular dynamics investigation[J].
Phys Chem B, 1999(103): 1161-1166.
|
| [10] |
CHALARIS M, SAMIOS J. Translational and rotational dynamics in supercritical methanol from molecular dynamics simulation[J].
Pure and Applied Chemistry, 2004(76): 203-213.
|
| [11] |
CHEN B, POTOFF J J, SIEPMANN J I. Monte carlo calculations for alcohols and their mixtures with alkanes.transferable potentials for phase equilibria.5. United-Atom description of primary secondary and tertiary alcohols[J].
Phys Chem B, 2001(105): 3093-3104.
|
| [12] |
AND I Y G, PIOTROVSKAYA E M. Properties of coexisting phases for the ethanol-ethane binary system by computer simulation[J].
Journal of Physical Chemistry B, 1999, 103(36): 7681-7686.
DOI:10.1021/jp990263j |
| [13] |
陈正隆, 徐为人, 汤立达.
分子模拟的理论与实践[M]. 北京: 化学工业出版社, 2007, 6.
|
| [14] |
ALLEN M P, TILDESLEY D J.
Computer simulation of liquids[M]. Oxford: Clareendon Press, 1987, 327-341.
|
| [15] |
DE-LEEUW S W, PERRAM J W, SMITH E R. Simulation of electrostatic systems in periodic boundary conditions Ⅰ Lattice sums and dielectric constant[J].
Proc R Soc Lond A, 1980(373): 27-56.
|
| [16] |
RYCHAERT J P, CICCOTTI G, BERENDSEN H J C. Numercial intergration of the cartesian equations of motion of a system with constraints:molecular dynamics of n-alkanes[J].
J Chem Phys, 1977(23): 327-341.
|
| [17] |
GEAR C W. Numerical integration of ordinary differential equations[J].
Mathemetics of Computation, 1967, 21(98): 146-156.
DOI:10.1090/S0025-5718-1967-0225494-5 |
| [18] |
李勇, 刘锦超, 芦鹏飞, 等. 从常温常压到超临界乙醇的分子动力学模拟[J].
物理学报, 2010, 59(7): 4880-4887.
DOI:10.7498/aps.59.4880 |
| [19] |
DILLON H E, PENONCELLO S G. A fundamental equation for calculation of the thermodynamic properties of ethanol[J].
International Journal of Thermophysics, 2004, 25(2): 321-335.
DOI:10.1023/B:IJOT.0000028470.49774.14 |
| [20] |
PETRAVIC J, DELHOMMELLE J. Influence of temperature, pressure and internal degrees of freedom on hydrogen bonding and diffusion in liquid ethanol[J].
Chemical Physics, 2003, 286(2/3): 303-314.
|
| [21] |
DELLIS D, MICHALIS C A, SAMIOS J. Pressure and temperature dependence of the hydrogen bonding in supercritical ethanol:A computer simulation study[J].
Journal of Physical Chemistry B, 2005, 109(39): 18575-18590.
DOI:10.1021/jp051688a |
| [22] |
周晓平, 杨向东, 刘锦超. 超高压水的分子动力学模拟[J].
高压物理学报, 2009, 23(4): 1-5.
|
| [23] |
KARGER N, VARDAG T. Temperature dependence of self iffusion in compressed monohydric alcohols[J].
Journal of Chemical Physics, 1990, 93(93): 3437-3444.
|
 2018, Vol. 44
2018, Vol. 44