文章信息
- 王京, 何华锋, 李天梅, 徐从启, 杨宗浩, 韩聪聪
- WANG Jing, HE Huafeng, LI Tianmei, XU Congqi, YANG Zonghao, HAN Congcong
- 基于Fisher统计量的测试性增长试验数据相容性检验方法
- The method of compatibility check of testability growth test data based on Fisher-statistics
- 中国测试, 2017, 43(8): 11-13, 40
- China Measurement & Test, 2017, 43(8): 11-13, 40
- http://dx.doi.org/10.11857/j.issn.1674-5124.2017.08.003
-
文章历史
- 收稿日期: 2016-09-22
- 收到修改稿日期: 2016-11-18
2. 解放军总后勤部建筑工程技术研究所, 陕西 西安 710032
2. The Institute of Construction Engineering Research, General Logistics Department of PLA, Xi'an 710032, China
测试性是指装备能及时、准确地确定其状态并隔离其内部故障的一种设计特性[1-3]。仅通过收集的现场数据对测试性水平进行评估,往往难以获得高准确度、高置信度的评估结论。因此研发人员通常将除现场数据以外的其他各类信息,如历史数据、专家经验数据、增长试验数据等,也都加以利用[4]。这些数据来自装备全寿命周期的不同层级、不同阶段,具有不同的形式,在统计上具有一定的差异[5-6]。因此在利用多源数据进行评估之前,首先需要对数据进行相容性检验,即检验其与现场数据的总体一致性,否则基于该数据得到的评估结论不可信[7]。
需要进行相容性检验的测试性信息种类繁多,其中很重要的一类就是增长试验数据。此类数据的获得贯穿于装备全寿命周期,反映了装备的发展进步,但数据量一般较小,属于“小子样”的情况,且具有成败型二值特点[8]。适用于此类数据的检验方法,在可靠性领域多有研究。文献[9-11]认为在分布未知的情况下,Wilcoxon秩和检验法比较有效,可直接用于相容性检验;文献[12]提出的K-S检验法比秩和检验法结果更加严谨,可用于开展评估。也有不少文献沿用显著性检验相关方法,将Konmotopob方法、判别分析方法、矩检验法等策略引入相容性检验,对样本进行处理。已有的检验方法多是在可靠性背景下提出的,对于测试性增长试验数据这类规划性强、增长趋势明显的数据,其适用情况说明还不够明确。且此类数据以“小子样、成败型”呈现,通用的检验方法对其独特的数据特征提取不够明显,因此有必要针对性地提出相应的相容性检验方案。
根据以上研究现状,结合测试性增长试验数据的特点,本文提出了基于Fisher统计量[13-15]的非参数相容性检验方法。首先利用序化模型对增长试验各阶段进行增长趋势验证,然后计算相邻阶段Fisher统计量值,判定其连带关系,最后给出相应的检验结论,并就增长阶段和样本数对检验成败的影响进行讨论。
1 增长趋势验证测试性增长试验是通过试验和使用,发现装备或单元存在的问题,并采取改进措施,使故障诊断能力得到提升的一类试验[16]。目前得到的测试性增长试验数据为单个增长阶段的成败型试验数据,其数据量较小,分布参数不固定,属于“小子样、异总体”的情况。针对此类数据的特点,研究提出基于Fisher统计量的测试性增长试验数据相容性检验策略。
假设装备在得到最终评估指标结论之前,经历了m个增长阶段,每个增长阶段的故障检测率水平用qi(i=1,2,…,m)表示,最终装备的所处阶段记作第m+1阶段。为完成增长基本任务,当测试性增长试验的效果良好时,应存在如下顺序约束模型:
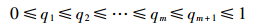 |
(1) |
该模型主要用于判断增长过程是否存在明显增长趋势。
2 基于Fisher统计量的相邻阶段连带关系判定结合检验所需,在连带关系判定上提出假设H0与其备择假设H1:
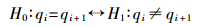 |
(2) |
首先,将相邻阶段的成败型试验数据写成列联表形式,如表 1所示。
对上表进行分析处理,计算其超几何分布概率:
 |
(3) |
将上表所有排列的超几何分布概率之和记为P,分下列两种情形进行讨论分析。
1)若fi+1/ni+1<fi/ni,Fisher统计量用多个阶段的超几何分布概率表示为
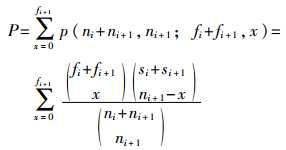 |
(4) |
为使式(4)排列计算能够得到实数范围内结果,应满足如下约束:
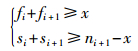 |
(5) |
2)若fi+1/ni+1>fi/ni,则:
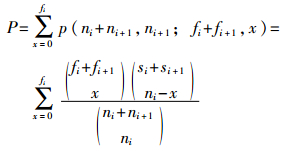 |
(6) |
为使式(6)排列计算能够得到实数范围内结果,应满足如下约束:
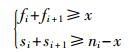 |
(7) |
实际应用中显著性水平通常取α≤0.2;如果已经证明武器装备故障检测水平存在增长,则α可取0.3或0.4,甚至更高[4]。
上述模型主要适用于小子样情况,通过仿真发现,当样本数超过26之后,上述模型将不再适用。分析其原因,主要是样本量增大之后,约束式(5)和式(7)将不再满足。而且由于排列中涉及到阶乘运算,当排列的基数较大时,计算上将比较困难。
在取定α前提下,如果满足P>α,表明相邻阶段故障检测率指标之间没有显著的连带关系,此时接受假设H0;如果P≤α,则接受假设H1,认定相邻阶段故障检测率指标之间具有明显的连带证据,说明存在相互关联。
当装备全寿命周期经历的增长阶段较少时,统计到的数据相对较少,不利于对装备整体状态和性能的认知,但如果如期完成增长任务,则可说明装备每次改进较为明显,能较快达到所要求的水平;当装备全寿命周期经历的增长阶段较多时(多指经历了7个以上增长阶段),那么收集到的增长试验数据相对较多,对装备的认知也更全面,但每次改进幅度相对有限。两种情况具体优选,应结合研制和改进代价,依据故障注入试验样本数多少具体而定。本文结合实例应用,给出了工程建议。
3 实例应用某型导弹综合测试模拟训练系统,在研制过程中,统计到的一个经历3次大的性能提高。1)联调初期,第1次通电整体测试,发生5次故障,且都未能成功检测到。5次故障之后,装备因故无法继续运行。2)第2次初样通电测试,经维修确认共发生7次运行故障,只成功检测到4次。而后分析原因,对测试装备进行进一步的改进提高。3)进行样机完整测试,要求达成所有任务请求,统计到整个运行过程中,一共发生10次故障,有2次未能成功检测。故障能否被检测到主要依据于已知故障模式的屏幕提醒。装备列装前进行验证测试,注入12个故障均能做出正确预报。
通过上述过程,统计到增长试验数据(5,5),(7,4),(10,2)和最终阶段试验结果(n4,f4)=(12,0)。
首先,计算各个增长阶段的点估计值,分别为:q1=0,q2=42.86%,q3=80.00%,q4=100%,满足式(1)所示的顺序约束模型,说明各阶段间具有明显增长趋势。
其次,通过Fisher统计量对相邻阶段间的连带关系进行判定。在α0=0.2的情况下,将增长数据带入上述检验模型,计算出第1阶段到第2阶段的Fisher统计量P1≈0.156<0.2,第2、3阶段间Fisher统计量P2=0.145<0.2,第3阶段到最终结果的Fisher统计量值P3=0.195<0.2,则接受备择假设H1,说明各相邻阶段间具有显著的连带关系。
最后得出结论,该组测试性增长试验数据通过相容性检验。
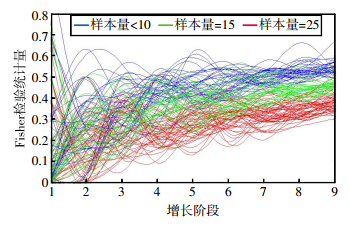
以Fisher检验统计量为指标量值,通过计算机仿真,给出了增长阶段数对检验通过与否情况的关系,如图 1所示。
|
| 图 1 增长阶段、样本量与Fisher统计量关系图 |
由图可知,当增长阶段数较少时,随着样本量的增加,Fisher检验统计量变化不明显;而后随着增长阶段数的增加,Fisher检验统计量呈缓慢增大趋势。但随着增长阶段数的增加,当评估的样本量变大时,Fisher检验统计量值就相对变小,更容易通过检验。在实际中,样本量越大,一般得到的结果也越可信,这与上述结论基本一致。因此在条件允许的情况下,尽可能增加样本量是得到可信结果的首选。
当增长阶段数据安排过少时,检验结果偶然性太大;增长阶段安排过多时,维修改进的成本将增多。因此工程实际中,在给定显著性水平的情况下,应综合考虑增长成本、结果稳定性、维修改进技术水平等因素的影响,合理安排装备增长过程中的增长阶段数。
4 结束语本文研究了一种基于Fisher统计量的测试性增长试验数据非参数相容性检验方法,并得出以下主要结论:
1)提出的Fisher统计量检验法针对性较强,主要解决了“小子样、成败型”数据的相容性检验问题。
2)针对增长试验数据,结合数据特点,分别对增长趋势和连带关系进行判定,检验思路更加完整。
3)通过讨论分析,验证了样本量越充足越容易通过相容性检验的结论;具体的增长阶段数应结合实际情况进行合理安排。
| [1] | 中国航空工业总公司三〇一所. 装备测试性大纲: GJB 2547-1995[S]. 1996. |
| [2] | 田仲, 石君友. 系统测试性设计分析与验证[M]. 北京: 北京航空航天大学出版社, 2003: 173-182. |
| [3] | 张伟昆. 测试性分析与评估体系的研究[J]. 国外电子测量技术, 2015, 34(5): 38–42. |
| [4] | 常春贺, 杨江平, 曹鹏举. 基于研制信息的测试性验证试验方案研究[J]. 航空学报, 2012, 33(11): 2057–2064. |
| [5] | 徐萍, 刘松林, 李勇. 测试性试验概念及模型研究[J]. 计算机测量与控制, 2006, 14(9): 1149–1152. |
| [6] | 李天梅. 装备测试性验证试验优化设计与综合评估方法研究[D]. 长沙: 国防科学技术大学, 2010. |
| [7] | 刘晗, 郭波. 小子样产品可靠性Bayes评定中的相容性检验方法研究[J]. 机械设计与制造, 2007(5): 165–166. |
| [8] | LI T M, XU C Q, QIU J, et al. The assessment and foundation of bell-shaped testability growth effort functions dependent system testability growth models based on NHPP[J]. Mathematical Problems in Engineering, 2015, 2015: 1–17. |
| [9] | 李鹏波, 张士峰, 蔡洪. 导弹仿真试验结果静态一致性检验及其置信度[J]. 现代防御技术, 1999(6): 31–36. |
| [10] | 张湘平, 曹国敏. 验前信息与现场子样的相容性检验方法研究[J]. 飞行器测控学报, 2002, 21(1): 55–59. |
| [11] | 张金槐. 多源信息的Bayes融合精度鉴定方法[J]. 国防科技大学学报, 2001, 23(3): 93–97. |
| [12] | 胡正东, 曹渊, 张士峰, 等. 特小子样试验下导弹精度评定的Bootstrap方法[J]. 系统工程与电子技术, 2008, 30(8): 1493–1497. |
| [13] | 茆诗松. 统计手册[M]. 北京: 科学出版社, 2003: 177-185. |
| [14] | LOVE J J. Fisher statistics[C]//Encyclopedia of Geomagnetism and Paleomagnetism Springer Netherlands, 2007. |
| [15] | 李明明. Fisher与小样本及"n维几何法"[D]. 天津: 天津财经大学, 2014. |
| [16] | LIN T C. Development of U.S. air force international ballistic missle weapon systems[J]. Journal of Spacecraft and Rockets, 2003, 40(4): 491–509. DOI:10.2514/2.3990 |
 2017, Vol. 43
2017, Vol. 43