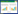文章信息
- 郭培培, 董浩斌, 葛健, 罗望
- GUO Peipei, DONG Haobin, GE Jian, LUO Wang
- Overhauser磁力仪低噪声信号处理技术
- Low noise signal processing technology of Overhauser magnetometer
- 中国测试, 2017, 43(6): 123-128
- China Measurement & Test, 2017, 43(6): 123-128
- http://dx.doi.org/10.11857/j.issn.1674-5124.2017.06.026
-
文章历史
- 收稿日期: 2016-10-15
- 收到修改稿日期: 2016-12-03
2. 武汉中地资环工研院管理有限公司, 湖北 武汉 430074
2. Wuhan Industrial Technology Research Institute of Geo-resources and Environment Co., Ltd., Wuhan 430074, China
地磁场是非常微弱的矢量场,是由各个不同来源的磁场叠加构成,在全球不同位置不同高度的磁场信息也是不同的[1]。地磁场测量是人类开发矿产资源,了解地质结构的重要手段。因此,研究高精度的磁场测量装置具有现实意义。质子磁力仪由于其操作简易,体积小,稳定性出众,是当今使用最广泛的地磁勘测仪器之一[2-3],但存在精度低、功耗大等问题。随后,经过改进后的Overhauser效应质子磁力仪降低了功耗,提高了精度和灵敏度[4-5]。然而改进后的信号仍然非常微弱,峰峰值最大仅2 μV,因此微弱信号的提取和处理是该类仪器的关键。目前国内投入使用的Overhauser磁力仪均通过国外进口,主要包括加拿大GEM公司GEM-19系列和俄罗斯POS系列,我国对Overhauser磁力仪的研究起步较晚,还处于实验研究阶段。
为提高磁力仪性能,相关学者主要从提高探头输出信号强度和频率测量精度两方面开展研究。文献[6-8]从频率测量角度入手,从时域和频域上设计了多通道测频算法和频谱分析算法,一定程度提高了测量精度,但没有根本解决FID信号信噪比的问题;文献[9-10]分析了探头噪声和仪器噪声来源,但没有提出降噪解决方案。文献[11-12]从射频激发角度入手,设计优化射频电路和提高溶液的极化程度来提高探头输出信号强度,但对于输出FID信号的处理没有给出具体的方案。
针对上述问题,本文首先介绍测量原理和系统结构,然后建立系统噪声模型,详细分析噪声对测量带来的影响,给出低噪声信号处理方案,并测试仪器噪声水平。通过实验,实现了地磁场测量,有效提高了磁场测量精度。
1 测量原理Overhauser磁力仪选用自由基溶液作为工作物质。自由基溶液是一种富含未配对电子的物质,化学性质非常不稳定,是现代电子顺磁共振的主要研究对象之一[13]。Overhauser磁力仪采用动态核极化的方式,利用高频振荡器产生满足电子自旋共振频率的射频信号作用于探头,电子系统产生电子自旋共振,带动自由基溶液中的质子系统产生极化;一段时间后,撤去射频激发,对探头加一短暂直流场源后,由于弛豫作用,溶液中大量被激发的质子将绕着地磁场做旋进运动,形成拉莫尔进动信号,如图 1所示。
|
| 图 1 Overhauser效应极化过程 |
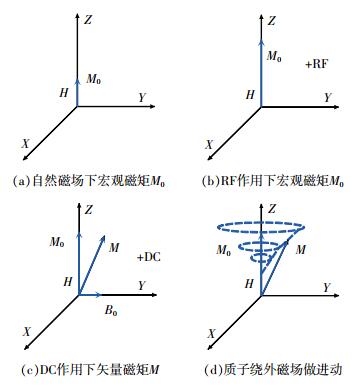
通过物理分析表明,质子旋进信号表达式为
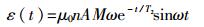 |
(1) |
式中:μ0——磁导率,rad/(s·T);
n——线圈匝数;
A——线圈截面积,m2;
M——质子磁化强度,A/m;
T2——横向弛豫时间,s;
ω——拉莫尔角频率,rad/s。
从表达式可以看出,探头输出信号为指数衰减的拉莫尔频率信号,仅考虑输出信号最大值情况,则:
 |
(2) |
又有旋进角速度ω与地磁场H成正比,其关系式为
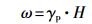 |
(3) |
其中γp是质子的磁矩与动量矩的比值,又称质子的磁旋比,是一个常数。又根据ω=2πf,f为拉莫尔旋进运动的频率,可得:
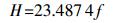 |
(4) |
地磁范围为20~100 μT,探头输出信号峰峰值范围为0.4~2 μV,对应频率范围为850~4 300 Hz。由此,将磁场测量转换为旋进信号频率的测量。
2 噪声分析由于探头输出的信号十分微弱并包含噪声,为提高测量精度,对系统的噪声进行建模分析是十分必要的,其模型示意图及噪声来源如图 2所示。可以看出,探头产生的拉莫尔信号经过屏蔽电缆接入放大器后有两个噪声来源:感应噪声和电路自身噪声。
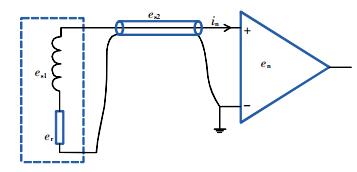
|
| 图 2 探头与放大器噪声模型 |
感应噪声指探头中的电感感应噪声es1和屏蔽电缆感应噪声es2两部分,这类噪声与外部电磁环境有关,无法通过理论计算,但可以采取相应措施尽量减小,如使探头中两个电感参数相同,对探头进行电磁屏蔽(不是磁屏蔽),信号线的屏蔽层采用单点接地措施等。对于电路自身而言,其噪声是可定量计算的。从图 2可知,电路自身噪声有3个来源:探头中电感的内阻R产生的热噪声er、放大器的输入噪声电流in流过探头电感内阻R产生的噪声,放大器自身输入噪声电压en。则总噪声功率可表示为
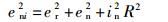 |
(5) |
用其有效值的平方可表示为
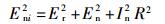 |
(6) |
电阻热噪声电压有效值可表示为
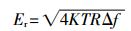 |
(7) |
式中:K——波尔兹曼常数,J/K;
T——绝对温度,K;
R——电阻阻值,Ω;
Δf——等效频带宽度,Hz。
本文研究中待测信号等效噪声频带宽度[11]为
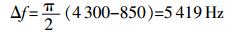 |
(8) |
此时,图 2等效模型中电路总噪声表达式为
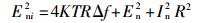 |
(9) |
对于低噪声放大器,In数值较小,输入总噪声Eni的主导成分是放大器本身噪声En和电阻R的热噪声Er。通过式(6)~式(8),电路总噪声有效值为
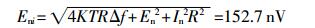 |
由上文分析,输出信号最小峰峰值为0.4 μV,探头输出信号信噪比为
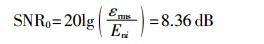 |
由此可见,Overhauser磁力仪探头输出信号极为微弱、信噪比较低。为提高磁场绝对测量精度,必须降低噪声带宽提高信号信噪比。同时,系统包含多种噪声源,针对不同的噪声来源应采取不同的措施。
3 信号调理Overhauser磁力仪结构由探头、激发模块、信号调理电路以及测频单元构成。系统控制单元采用STM32处理器,系统结构如图 3所示。探头由自由基溶液、激励线圈和接收线圈组成,用于产生质子旋进信号。
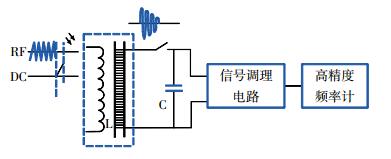
|
| 图 3 系统结构图 |
3.1 谐振设计
探头输出的拉莫尔信号为感应信号,若直接通过放大器进行处理,放大器会引入额外的噪声,不能压制探头自身输出的噪声带宽。相比较而言,在探头输出端加上可变电容,使电感与电容电路发生谐振,在增加输出信号的幅度的同时抑制谐振带宽以外的噪声,从而使传感器输出信号信噪比增加。本文选用等效电阻最小的串联谐振方式,示意图如图 4所示。图中L为电感,Cx为可变调谐电容,R为探头电阻。
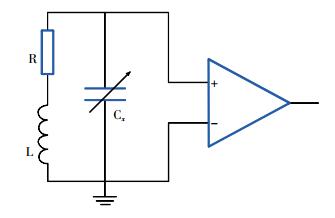
|
| 图 4 串联谐振示意图 |
串联谐振如下式所示:
 |
(10) |
式中:f——谐振回路的中心频率,Hz;
L——探头的电感量,H;
Cx——调谐电容值,F。
谐振回路的品质因数Q为
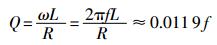 |
(11) |
设计的探头参数为L=34 mH,R=19 Ω,谐振回路的带宽计算公式为
 |
(12) |
假设探头输出拉莫尔频率信号有效值为Vs,结合式(7)可得出谐振之前探头输出信号信噪比为
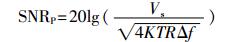 |
(13) |
探头谐振后,输出信号有效值变为QVs,带宽内的噪声也增加了Q倍,其噪声带宽如式(12)所示,所以此时输出信号信噪比为
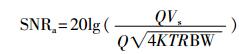 |
(14) |
由式(13)和式(14)可得出利用串联谐振使探头输出信号的信噪改善比(SNIR)为
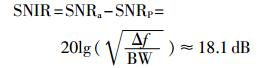 |
(15) |
即串联谐振之后探头输出信号的信噪比增加了18.1 dB。结合探头输出信号公式(2),可得探头输出信号经过谐振之后的信号幅度为
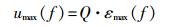 |
(16) |
实际上,由于电感线圈的趋肤效应会使谐振品质因数Q降低,导致谐振后实际信号峰值比式(16)的理论计算结果低很多,且频率越高,趋肤效应越大,Q下降越厉害,两者之差也越大,但其变化趋势保持一致,呈线性增长。
探头谐振后,由于谐振时使频率带宽变窄(谐振后带宽为84 Hz),为了能够在有效频带内使探头谐振,利用可变电容对探头进行调谐。待测磁场的测量量程是20~100 μT,对应频率范围是850~4 300 Hz,探头的电感量为34 mH,按照式(10)计算出的调谐电容范围为28~1 022 nF。通过对10个模拟开关不同组合,实现在1~1 023 nF范围内,以1 nF为分辨率,电容值任意可调,满足计算结果要求。
3.2 放大器设计探头输出信号经过谐振放大处理后,仅减小了信号源内阻R产生的热噪声VR的带宽,而放大器自身的噪声带宽并未受到限制,所以为了对放大器自身带宽进行限制,采用窄带滤波的方法来实现。
设计多级级联放大器,根据微弱信号检测理论弗里斯公式可知[14]:对多级级联放大器而言,第1级放大器的噪声系数对总噪声系数影响最大,所以必须保证第1级放大器的噪声系数足够小。因此,前置放大器的器件选择和电路结构是至关重要的。探头输出信号通过谐振回路后,信号幅度在850~4 300 Hz内不是一个固定值,而是处于2~35 μV之间。为了获得良好的测频精度及分辨率,设计放大后的拉莫尔信号幅度为1.5 V,以满足迟滞比较器门限电压。
放大器输出信号噪声与整形后方波信号的抖动量有如下关系:
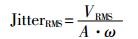 |
(17) |
式中:JitterRMS——整形后的方波信号的有效值抖动量;
VRMS——噪声均方值;
A——信号的峰值;
ω——信号的角频率。
信号的信噪比越高,整形后方波的抖动量就越小。在本文中,如果信号的本底噪声是10 mV(有效值),信号的幅度是1 V,频率是1 kHz。那么整形后方波的抖动量约为1.5 μs。如果测频的积分时间为1 s,那么这个抖动量将会导致0.001 Hz的测频噪声,即0.02 nT的测磁噪声。
放大器噪声与输出噪声的关系如下式所示:
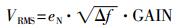 |
(18) |
式中:VRMS——放大器输出噪声均方值,V;
eN——等效输入噪声平均谱密度,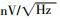
GAIN——放大器的增益。
已知放大器等效噪声带宽为5 419 Hz,平均放大倍数约为200 000,根据放大器动态范围,输出噪声有效值约为10 mV,则放大电路的等效输入噪声须小于0.67 
本次设计采用超低噪声的JFET为前置放大器件,对其单独稳压供电,避免其他干扰通过电源对其产生影响。第2级为两个参数相同的同相选频放大,使信号幅度在频带范围内为固定值或变化较小,将微伏级信号放大至伏级。第3级窄带滤波,选用开关电容滤波芯片配合控制器,实现自跟踪功能,限制信号中的噪声带宽以提高信号信噪比。如图 5所示为放大器结构示意图。
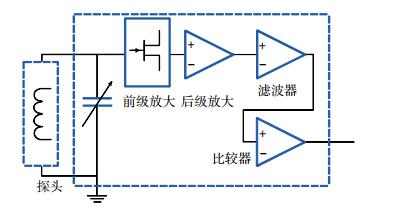
|
| 图 5 放大器结构图 |
4 测试与分析 4.1 热噪声测试
根据所建立的噪声模型,仪器噪声主要来源于探头电感的电阻热噪声。为了验证模型的建立及理论分析的正确性,首先将放大器输入端接A端,测量电路本底噪声;然后断开A端接入B端,将探头接入放大器,测量探头引入噪声如图 6所示。测量结果如表 1所示。
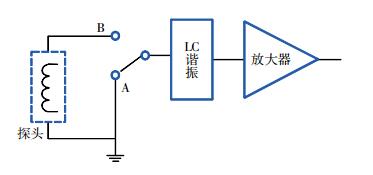
|
| 图 6 热噪声测试方案图 |
通过表 1实验数据可以看出,在高增益情况下,仪器接入探头后,总体噪声有明显增加。同时可知,仪器噪声在纳伏级,电压噪声不随频率变化的量,电感的电阻噪声是仪器噪声的主要来源,验证了理论分析的正确性,为调理电路的设计提供了依据。
4.2 放大器测试通过上文分析,探头输出的拉莫尔信号在850~4 300 Hz频带内不是固定值,而是处于2~35 μV之间。为了测试放大器自身噪声带宽限制能力,选取2 μV输入信号进行测量。利用信号源输出峰峰值为200 mV,频率范围850~4 300 Hz的正弦波,根据阻抗匹配原则[15],选取图 7所示测试方案,经过衰减网络后信号峰峰值为2 μV。首先接通图 7中的A端,测出放大器增益特性,结果如图 8所示。断开A端接通B端,测出放大器输出端噪声有效值,计算系统信噪比。
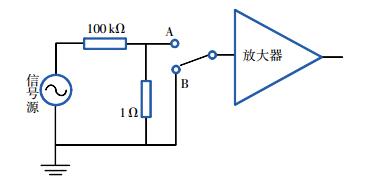
|
| 图 7 测试方案示意图 |
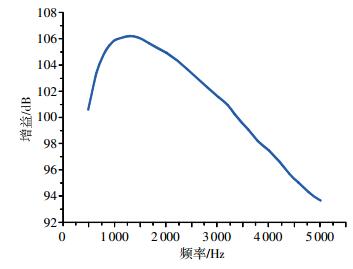
|
| 图 8 放大器增益特性曲线 |
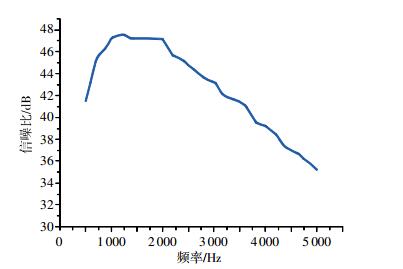
通过图 8可以看出,在有效频带850~4 300 Hz内,放大器增益均大于92 dB,呈线性关系,与理论分析相符合;在频带外,放大增益有明显衰减,验证了所设计的放大器的选频放大特性,能够有效限制放大器自身噪声带宽。选取幅度为2 μV的信号,计算放大器信噪比,如图 9所示。可以看出,放大器输出后信噪比在有效频带内大于36 dB。
|
| 图 9 信噪比曲线 |
4.3 室外对比测试
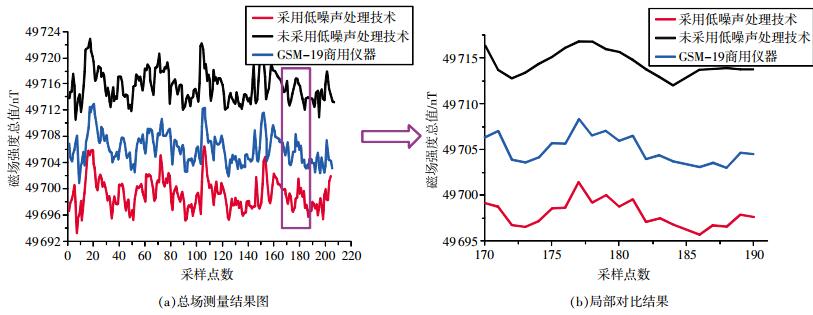
为更好地体现仪器的性能,将未采用本文提出的降噪处理技术的测量装置和采用本文提出的低噪声处理技术的测量装置与国外商用仪器在野外进行对比实验。使用加拿大GEM公司的GSM-19系列Overhauser磁力仪作为标准仪器,其绝对测量精度±0.1 nT,分辨率0.01 nT。实验时,3种仪器同时开机测试,避免由于时间不同造成的磁场强度偏差,传感器相隔一定距离,避免相互影响磁场的分布,保证测试的有效性。记录同一段时间内的磁场变化,结果如图 10所示。
|
| 图 10 总场测量与局部对比结果图 |
从图可以看出,3种测量装置在同一时间内测量曲线基本一致。为了更加充分地验证本文提出的降噪措施的有效性,选取图 10(a)中局部点数进行观察,如图 10(b)所示。当磁场存在微小变化时,采用本文提出的信号处理技术的测量装置能灵敏地跟踪到微小变化量,测量精度与商用仪器基本一致,而未采用低噪声处理技术的测量装置,无法准确检测出微小变化量,只能体现大体趋势以及较大异常变化。通过对整体测量数据分析与计算,本文设计的Overhauser磁力仪测量精度为0.2 nT,已经接近商用磁力仪,证明了在磁场测量中的可靠性。
5 结束语低噪声信号处理是Overhauser磁力仪的关键技术。本文首先详细分析了系统噪声模型,针对不同来源噪声设计了低噪声信号调理方案包括LC谐振电路和低噪声放大器。然后选择超低噪声的JFET器件作为前置放大器,同时设计选频放大结构降低系统噪声,提高了测量精度。最后对比分析了本装置和商用仪器测量磁场的性能,通过实验数据验证了此设计方法的可行性。在今后Overhauser磁力仪研究中将采取低噪声信号处理技术和高精度频率测量算法结合的方案,进一步提高Overhauser磁力仪的测量精度和稳定性。
| [1] | 傅慷, 余杰, 钱富. 地磁导航的相关技术研究[J]. 船电技术, 2013, 33(4): 31–33. |
| [2] | 董浩斌, 张昌达. 量子磁力仪再评说[J]. 工程地球物理学报, 2010, 7(4): 460–470. |
| [3] | HRVOIC I, NEWITT L R. Instruments and methodologies for measurement of the earth's magnetic field[M]∥MANDEA M, KORTE M. Geomagnetic Observations and Models. Springer, 2011:105-126. |
| [4] | SHIM J H, LEE S J, HWANG S, et al. Proton spin-echo magnetometer: a novel approach for magnetic field measurement in residual field gradient[J]. Metrologia, 2015, 52(4): 496–501. DOI:10.1088/0026-1394/52/4/496 |
| [5] | DENISOV A Y, SAPUNOV V A, RUBINSTEIN B. Bro-adband mode in proton-precession magnetometers with signal processing regression methods[J]. Measurement Science & Technology, 2014, 25(5): 55103–55108. |
| [6] | 刘欢, 董浩斌, 葛健, 等. 基于Overhauser效应的磁场梯度探测器[J]. 仪器仪表学报, 2015, 36(3): 592–600. |
| [7] | DONG H B, LIU H, GE J, et al. A high-precision frequency measurement algorithm for FID signal of proton magnetometer[J]. IEEE Transactions on Instrume-ntation & Measurement, 2016, 65(4): 898–904. |
| [8] | PENG Y, GE J, ZHOU S. A frequency-measurement technology of larmor precession signal in overhauser magnetometer based on spectrum zoom algorithm[J]. Icic Express Letters, Part B: Applications An International Journal of Research & Surveys, 2015, 10(6): 2635–2642. |
| [9] | ZHENG D D, WANG Y, JIAO Y, et al. Analysis and detection of Overhauser magnetometer signal[J]. Applied Mechanics & Materials, 2013(303/306): 1812–1817. |
| [10] | LIU T, GU L, ZHANG S, et al. Noise characteristics research of Overhauser magnetometer sensor[C]∥SPIE Optical Engineering+Applications. International Society for Optics and Photonics, 2015. |
| [11] | 谭超, 董浩斌, 葛自强. Overhauser磁力仪激发接收系统设计[J]. 仪器仪表学报, 2010, 31(8): 1867–1872. |
| [12] | ZHENG D, ZHANG S, FU H. An improved RF circuit for Overhauser magnetometer excitation[C]∥Radiation Detectors:Systems and Applications XVI, 2015. |
| [13] | KORTH, HANS-GERT. Electron spin resonance spectr-oscopy of organic radicals[J]. Angewandte Chemie, 2005, 43(19): 2469–2470. |
| [14] | 陈晓娟, 赵睿, 吴勇峰. 低频噪声测量方法的研究[C]∥中国仪器仪表学会第九届青年学术会议, 2007: 321-324. |
| [15] | 田亚朋, 张昌民, 仲维伟. 阻抗匹配电路原理与应用[J]. 电子科技, 2012, 25(1): 5–7. |
 2017, Vol. 43
2017, Vol. 43