文章信息
- 庞永丽, 郭亚静, 王黎明
- PANG Yongli, GUO Yajing, WANG Liming
- 基于混沌的水声定位信号设计及性能分析
- Design and performance analysis of underwater acoustic positioning signal based on chaos
- 中国测试, 2017, 43(10): 134-138
- China Measurement & Test, 2017, 43(10): 134-138
- http://dx.doi.org/10.11857/j.issn.1674-5124.2017.10.026
-
文章历史
- 收稿日期: 2017-03-12
- 收到修改稿日期: 2017-04-28
水声定位技术在军事领域和民用领域都具有广泛的应用前景。对于军事系统,水声定位技术有助于对敌方目标进行准确估计和精确打击;对于民用事业,例如在海洋资源探测和开发方面,精确的水下定位技术是探测和开发水下资源的关键技术。水声定位技术不仅能够对水下目标进行精确定位,而且还可以为水下机器人提供导航,这些都为水下工程提供了不少帮助。因此,对水下目标定位技术的研究对于国防建设和国民经济建设都具有重要意义。
在水声定位系统中,准确获得节点间的距离是精确定位的基础,文献[1]提出采用宽频混沌信号作为水声定位信号,与相应混沌匹配滤波器结合的方法来进行节点间的距离测量;文献[2]提出一种基于包络相关的水下动态节点测距方法。由于水声信道环境十分复杂,水声测距准确度易受到各种干扰及噪声的影响。扩频通信技术具有很强的抗干扰能力,将其应用于水下距离测量,能有效提高系统测距准确度[3]。
定位技术中,常用的测距方法有门限法、相移法、相关法、自干涉法[4],本文采用相关法进行水下测距。其原理是利用信号之间的自相关特性和互相关特性,一般来说,水听器接收到的有用信号与水声发射换能器发出的信号间的相关性号很强,而与噪声信号的相关性很弱,以此来区分淹没在噪声中的有用信号。具体做法是将水听器接收到的信号与水声发射换能器发出的信号进行相关运算,相关函数尖峰值所对应的延时时间就是水声信号由水声发射换能器传播到水听器所用的时间,从而可以得到两者之间的距离。
应用相关法进行测距的关键在于选取合适的伪随机序列作为扩频序列。传统的扩频序列采用的是m序列、Gold序列等,这些序列产生原理简单,易于实现,但存在可用码组数目少、序列复杂度低、互相关特性不理想等不足[5]。若将m序列作为扩频序列,由于其互相关函数存在许多峰值,导致系统抗多址干扰能力较弱,用作定位信号时,若一个水听器接收到多个水声发射换能器发出的信号,信号会产生混叠,难以区分,无法精确计算水听器到各个水声发射换能器间的距离。由于混沌序列对初值极其敏感,且自相关、互相关特性都十分理想,采用混沌信号作为声定位信号,能有效克服m序列的不足,不仅提高了两节点之间的定位准确度,而且能有效解决多址干扰对定位准确度的影响,适用于作为水声传感器网络节点的定位信号。
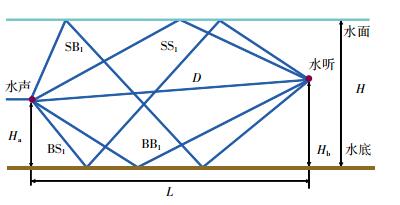
1 浅海水声信道模型建立在水声通信中,海洋就是声信道,是水下信息传输的媒介,声波在该信道传输时会有多种传播路径,且存在各种衰减。为了简化浅海水声信道模型,假设水深和水中的声速均为常数,水深记为H,水中的声速ν=1 500 m/s;浅海水声信道基本传播模型如图 1所示。
|
| 图 1 浅海水声信道基本模型 |
按照传播路径,将声线分成5种类型[6],第1类是直达声线,记为D;第2类是从水声发射换能器发出第1次反射经由水面,到达水听器时又是经过水面反射而来的声线,记为SSn;第3类是从水声发射换能器发出第1次反射经由水面,到达水听器时经过水底反射而来的声线,记为SBn;第4类是从水声发射换能器发出第1次反射经由水底,到达水听器时经过水面反射而来的声线,标志为BSn;第5类是从水声发射换能器发出第1次反射经由水底,到达水听器时又是经过水底反射而来的声线,记为BBn;n表示经过水底反射的次数。
直达声线传播的距离:
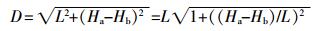 |
(1) |
由于H<<L,进行泰勒展开,可得:
 |
(2) |
取其前两项,可得:
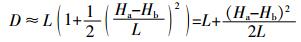 |
(3) |
式中:L——水声水听的水平距离;
Ha——水声距水底的深度;
Hb——水听距水底的深度。
同理,可得:
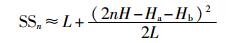 |
(4) |
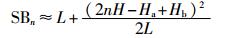 |
(5) |
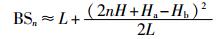 |
(6) |
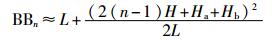 |
(7) |
各类声线每条路径的时延: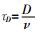
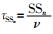
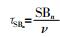
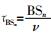
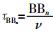
声波在水中的损耗主要有扩展损耗、吸收损耗和反射损耗3种[7]。对于浅海水声信道,由于传播距离r>>H,因此扩展损耗计算应采用柱面模型。根据不同波阵面的功率相同,即2πr1HI1=2πrHI,得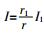

海水吸收损耗[8]:
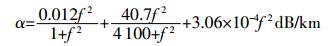 |
(8) |
其中f表示载波频率,单位为kHz,在波频率为30 kHz时,α=7.613 dB/km,则水声信号吸收损耗幅值衰减系数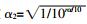
假设海底的反射系数rb=0.9;海面反射系数rs=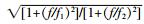

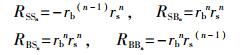 |
(9) |
其中,负号表示声波相位改变180°。
假设发送的调制后的混沌信号为x(t),则经水声信道后水听接收到的信号:
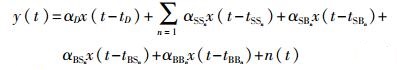 |
(10) |
式中αD=α1α2_D,αSSn=α1α2_SSn,αSBn=α1α2_SBn,αBSn=α1α2_BSn,αBBn=α1α2_BBn分别表示各条路径的衰减系数;α2_D=
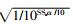
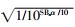
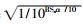
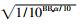
Logistic映射结构简单,性能优良,目前应用比较广泛,但是该映射产生的混沌序列在随机性方面仍存在一些不足。本文采用一种新型分段Logistic映射[9],该映射Lyapunov指数更大,混沌性更强,更适合作为扩频序列,该映射的表达式为
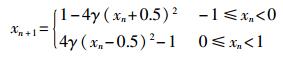 |
(11) |
当γ=2时,给定初始值x0,则根据式(2) 产生混沌序列{xn}。设序列{xn}由N个chip构成,为了减小对混沌序列类随机的破坏,直接对扩频码的chip频率进行调制,而不对混沌序列进行量化处理。扩频码型的第i个chip的中心频率可以表示为
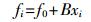 |
(12) |
式中:f0——系统中心频率;
B——系统带宽。
为了保证chip相位的连续性以减少有效带宽外频谱扩展,应进行相位平滑处理[10],即N个chip首尾相连构成所需的水声定位信号。相位满足的条件是:
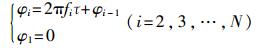 |
(13) |
式中φ1为chip的初始相位,τ为每个chip的脉宽,因此每个chip的波形可以表示为
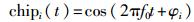 |
(14) |
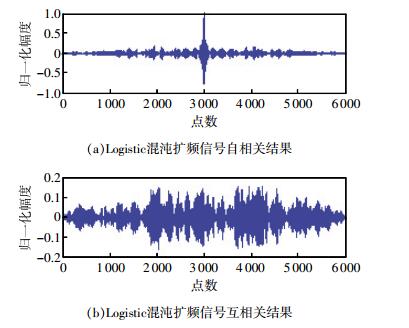
采用相关法进行测距,要求水声信号具有理想的相关特性,图 2、图 3分别显示了采用Logistic混沌序列和分段Logistic混沌序列作为扩频序列产生的扩频信号相关特性。
|
| 图 2 Logistic混沌扩频信号相关结果 |
|
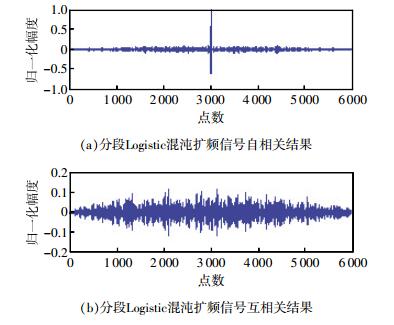
| 图 3 分段Logistic混沌扩频信号相关结果 |
对比两图可以看出,在序列长度为均为3 000时,采用分段Logistic混沌序列作为扩频序列产生的扩频信号,其相关特性更加理想,自相关函数具有明显的尖峰值,接近于δ函数,并且其互相关函数接近于0,易实现码分多址,适合作为水声定位信号[11]。
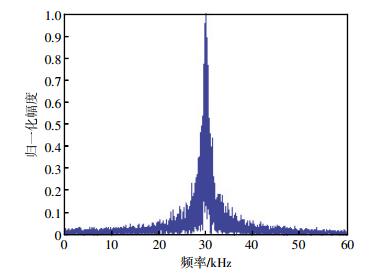
3.2 频谱分析由于水声信道可用带宽有限,所以对水声信号的带宽有一定的要求。图 4是该混沌扩频信号的频谱图,由图中可以看出,信号中心频率为30 kHz,带宽比较窄,带外频谱扩展较小,适用于水声通信系统。
|
| 图 4 混沌扩频信号频谱图 |
3.3 抗噪声及多址干扰能力分析
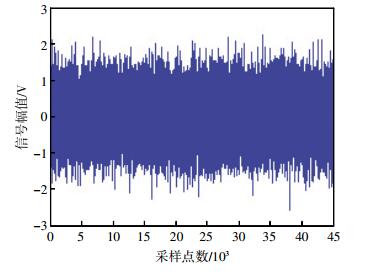
为了进一步了解该水声信号的抗噪声及抗多址干扰能力,进行以下仿真实验。仿真在浅水环境中进行,假设水深H=20 m;水声发射换能器A1~A6距水底深度均为10 m,水听器B距离水底深度Hb=3 m,水声发射换能器与水听器间的水平距离分别为La1b=50 m,La2b=60 m,La3b=70 m,La4b=80 m,La5b=90 m,La6b=100 m;水声定位信号的持续时长为20 ms,信号采样频率Fs=500 kHz,初始值分别取0.600,0.601,0.602,0.603,0.604,0.605,得到6组互不相关的信号x1(t)~x6(t),分别作为水声发射换能器A1~A6的输出信号。水听器B同时接收水声发射换能器A1~A6发出的信号,由于水声信道存在着各种噪声,水听器接收到的信号存在严重失真,在信噪比约为-20 dB的条件下,水听器接收到的信号如图 5所示。
|
| 图 5 水听器接收到的信号 |
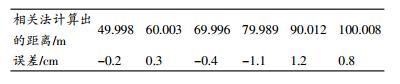
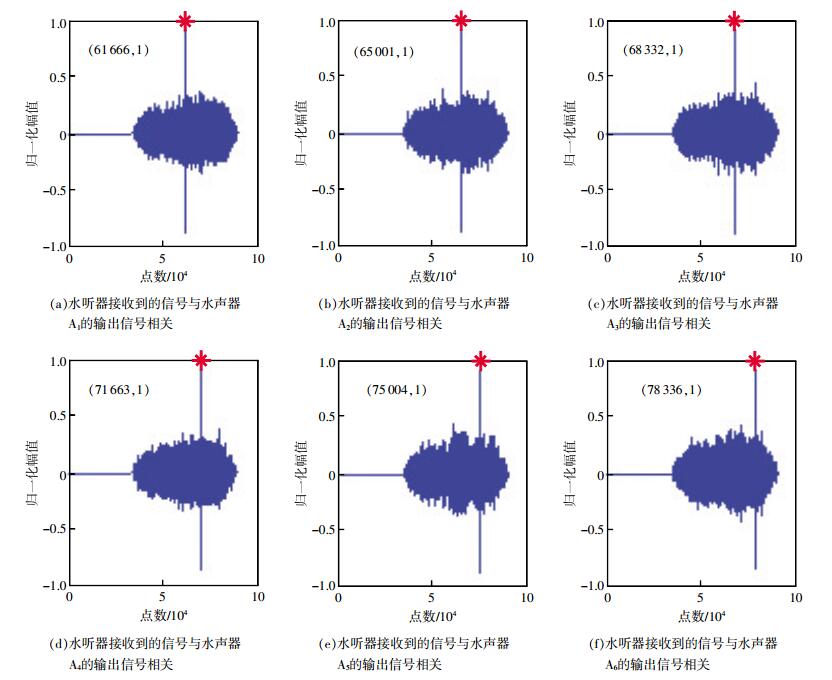
将水听器接收的信号分别与6组水声发射换能器发出的信号进行相关运算,结果如图 6所示,图中标记了相关结果峰值点的坐标。由该点对应的横坐标可以得到时差,从而可以计算出水听器B与各水声发射换能器之间的距离。假设两序列长度均为m,若无延时,则这两个序列相关后峰值所对应的点数为m,即为相关后总点数的一半[12]。根据图中结果,相关后总点数为90 000,所以在没有延时的条件下,峰值所对应的点数为45 000,则水声发射换能器A1到水听器B的距离s1为
|
| 图 6 水听器接收信号与6组水声器输出信号相关结果 |
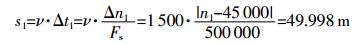 |
同样计算出A2~A6到水听器B的距离s2~s6,计算出的距离s1~s6及测量误差见表 1。由表可知,在水听器同时接收到多个信号,且在信噪比很小的条件下,仿真误差仍能控制在±2 cm之内,由此可以看出,使用该混沌扩频信号作为水声定位信号,不仅定位准确度高,而且能有效解决多址干扰对节点间距离测量的影响,适用于作为水下传感器网络节点的定位信号。
4 结束语
在水声定位系统中,水声器发出的信号在经水声信道传输时,易受到噪声及其他各种干扰的影响,导致信号失真,严重影响定位准确度。本文将混沌序列作为扩频码,经扩频调制产生的扩频信号作为声定位信号,不仅有效利用了混沌序列类噪声的特性,还发挥了扩频通信抗干扰能力强的优势。仿真结果显示,该信号的性能理想,抗干扰能力强,且容易实现码分多址,适用于作为水声定位信号。
| [1] |
任海鹏, 白超, 习亚平. 一种混沌水声定位方法[J].
仪器仪表学报, 2015, 36(6): 1227–1235.
|
| [2] |
郭亚静, 李宁, 姚金杰, 等. 一种基于包络相关的水下动态节点测距方法[J].
中国测试, 2016, 42(9): 96–100.
DOI:10.11857/j.issn.1674-5124.2016.09.020 |
| [3] |
王华亮, 邓伟, 景永刚. DS-SS在水声跟踪定位系统中的性能分析[J].
声学技术, 2010, 29(4): 424–427.
|
| [4] |
李博远. 基于混沌信号的超声波测距系统的研究与实现[D]. 南昌: 南昌大学, 2014.
http://cdmd.cnki.com.cn/Article/CDMD-10403-1014055301.htm
|
| [5] |
LI B Y, WANG Y H, KONG B. A novel sonar ranging method using discrete tent-map chaotic phase modulated Signal[J].
Journal of Computational Information Systems, 2013, 14(9): 5485–5493.
|
| [6] |
夏红燕, 徐志斌. 基于射线模型的水声传播衰减特性[J].
海军航空工程学院学报, 2012(6): 628–632.
|
| [7] |
惠俊英.
水下声信道[M]. 2版. 北京: 国防工业出版社, 2007: 106-109.
|
| [8] |
LI B, ZHOU S, STOJANOVIC M, et al. Multicarrier communication over underwater acoustic channels with no uniform doppler shifts[J].
IEEE Journal of Oceanic Engineering, 2008, 33(2): 198–209.
DOI:10.1109/JOE.2008.920471 |
| [9] |
张薇, 谢红梅, 王保平. 一种新型的分段Logistic混沌扩频通信算法[J].
计算机科学, 2013, 40(1): 59–62.
|
| [10] |
殷敬伟, 惠俊英, 王逸林, 等. M元混沌扩频多通道Pattern时延差编码水声通信[J].
物理学报, 2007, 56(10): 5915–5921.
DOI:10.3321/j.issn:1000-3290.2007.10.060 |
| [11] |
于银辉, 王玥. 混沌扩频序列的产生及其在CDMA中的应用[J].
吉林大学学报(信息科学版), 2004, 22(1): 23–26.
|
| [12] |
徐远明, 邵玉斌.
Matlab仿真在通信与电子工程中的应用[M]. 2版. 西安: 西安电子科技大学出版社, 2010: 308-316.
|
 2017, Vol. 43
2017, Vol. 43