文章信息
- 宁玉磊, 胡昌华, 周志杰, 李红增, 张正新
- NING Yulei, HU Changhua, ZHOU Zhijie, LI Hongzeng, ZHANG Zhengxin
- GPS信号校准晶振信号频率源误差在线修正方法
- Methods for correcting error of frequency source by GPS-Clock in calibration with crystal oscillator
- 中国测试, 2016, 42(4): 15-19
- CHINA MEASUREMENT & TEST, 2016, 42(4): 15-19
- http://dx.doi.org/10.11857/j.issn.1674-5124.2016.04.004
-
文章历史
- 收稿日期: 2015-09-03
- 收到修改稿日期: 2015-11-17
随着航空航天技术的不断发展,当前航天测控设备的计量测试越来越需要高准确度的时间频率标准。加之一些测试计量通常在野外条件下实施,环境特殊,也要求频率标准源能溯源简单、使用便捷。高准确度频标目前主要有铷钟、铯钟、氢钟等原子钟以及高准确度晶体振荡器;其中,氢、铯等原子钟频率准确度一般可达10-12~10-14,但价格昂贵,使用环境严格,难以普及。晶体振荡器短期稳定性好,使用寿命长、价格较为便宜,应用非常广泛,但长期稳定性较差,准确度一般为10-7~10-8,只能满足普通需求。GPS是目前世界上应用范围最广、实用性最强的全球精密授时、测距和导航定位系统。在每颗GPS卫星上都携带有原子钟,使GPS时间频率信号具有原子频标的长期频率稳定度[1]。采用GPS秒脉冲信号校准地面晶振的方法可获得短期及长期稳定度都很高的时间频率标准源,成本相对较低,可以实现对航空航天设备的便捷高效伴随计量,并且还能够进行野外条件下的自溯源。
GPS接收机接收GPS卫星发出的高准确度时间信息,提供全球统一的准确时钟。但由于GPS信号在传输过程中受星历误差、卫星钟差、电离层误差、对流层误差、多路径误差、接收机误差、跟踪卫星过少误差等因素的影响,会产生随机抖动,信号准确度和稳定性难以得到保证[2]。地面晶振由于受老化、温度等因素影响输出信号会包含随机误差和累计误差等频率偏移,同时在校准过程还会引入其他噪声。以上因素都会影响校频系统的输出频率准确度。实验表明如果不进行误差修正处理,校频系统的频率准确度最高只能达到1.0×10-8。
目前,对GPS校频的噪声误差处理方法较多,如文献[3]提出利用卡尔曼滤波算法来克服北斗卫星秒信号抖动及测量噪声,但该方法没有考虑晶振频率漂移的影响。文献[4]采取多次采样取平均的方法,对测量频差数据进行平滑处理,计算简单,易于实现,但校频时间较长。文献[5]提出了一种补偿方案较简单的高准确度时钟实现方法,但该方法的实时性不高,应用受到一定限制。文献[6]通过建立GPS信号与晶振信号的频差数学模型,利用最小二乘法估计出晶振信号的频率漂移系数,对误差进行在线补偿,但该方法所需样本数据多,计算较为复杂,且没有考虑GPS秒信号的野值对系统准确度的影响。
为解决上述问题,本文提出采用状态和参数联合估计的卡尔曼滤波算法对GPS校频过程中的GPS秒信号抖动误差、本地晶振误差、测量噪声进行处理,通过建立GPS信号校准晶振信号的频差数学模型,实时修正校频过程中的误差[7, 8]。同时对算法作了一定改进,通过滤波新息加权来消除GPS秒信号中野值对滤波的影响,使系统保持高准确度的频率输出[9]。该方法易于实现,已应用于某军用装备的计量和性能测试。
1 频差信号数学模型GPS卫星校准晶振的基本原理是将GPS接收机输出的秒信号与地面晶振分频后信号进行比对,获得相对频差,再将频差转换成控制修正电压,不断调节晶振的振荡频率,最终实现晶振高准确度和高稳定度的频率输出[1]。其基本原理如图 1所示。

|
| 图 1 GPS驯服地面晶振原理图 |
GPS接收机输出的GPS秒信号与国际标准时间(UTC)存在一定的误差ε,一般ε服从正态分布:

对于不同档次的GPS接收机,σ数值大小不同,如Motorola VPONCORE为50 ns,而GARMIN GPS 25/20则为1 μs。设定一时间序列K:1,2,3,4,…,k,…,n,其中k∈N。GPS接收机输出的秒信号序列Y对应的国际标准时间可记为

通用公式可表示为

εk——时间误差。
由于地面晶振的随机误差远小于GPS秒脉冲的随机误差(如准确度为10-9 s的晶振随机误差<1 ns),在此不考虑晶振分频信号的随机误差,仅考虑晶振的累积误差[9]。晶振分频输出秒信号产生的时间序列Y′对应的国际标准时间可记为

通用公式可表示为

b——频率漂移系数;
yk′——晶振分频输出第k个秒信号对应的国际标准时间。
则晶振分频信号的误差μk可表示为

那么晶振分频信号与GPS秒信号在k时刻的频率信号偏差:

GPS秒信号包含随机干扰ε、晶振信号包含频率偏移μ,导致频率偏差序列X′存有噪声干扰。为实现高精度频率输出,需要滤除X′中的ε、μ噪声误差,得到频率偏差X′的最优估计值。
2 卡尔曼滤波算法实现 2.1 卡尔曼滤波算法卡尔曼滤波适合解决最优线性滤波和估计问题,它以最小均方误差为准则,仅根据前一次估计值和最近一次观测数据就可估计信号的当前值,适用于实时处理[10]。频差噪声处理问题可以运用卡尔曼滤波算法来解决。
在本系统中,由频差模型式(3)推导可得状态方程:

观测方程:

令 ,原状态方程和观测方程转换为
,原状态方程和观测方程转换为

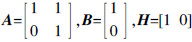 。
。
卡尔曼滤波过程为,先计算向前推算误差协方差Pk-:

计算卡尔曼增益Kk:

计算向前推算状态变量 :
:

由观测变量Zk更新估计值 :
:

更新误差协方差Pk:

一次完整的卡尔曼滤波完成。其中, k-为k时刻的先验状态估计,
k-为k时刻的先验状态估计, k-1为k-1时刻的后验状态估计,Pk-为k时刻的先验估计误差的协方差。
k-1为k-1时刻的后验状态估计,Pk-为k时刻的先验估计误差的协方差。
实际中需给定频差初值X0和估计误差协方差矩阵初值P0。其中X0可通过对一系列观察值平均计算得到。P0初值取为

模型噪声协方差矩阵Qk和观测噪声协方差矩阵Rk采用经验估计[11]。
2.2 新息序列加权卡尔曼滤波算法在实际应用中,只利用卡尔曼滤波算法消除随机噪声是不够的。由于GPS秒信号受噪声干扰还会产生较大跳变野值,带有野值的频差信号常常会使卡尔曼滤波算法对系统的状态预报进行错误修正,使滤波结果发生偏移,甚至发散。以往解决大都采用判别法,如3σ判别法等。这些判别方法有不足之处,如判别尺度选择等,当判出野值时,该时刻的信息如何处理,如果用估值代替,其结果是无法从观测值中得到新的信息,也就无法对估计状态进行修正,从而降低了滤波准确度。特别是当成片野值出现时,效果更差,甚至可能造成滤波发散。
为解决卡尔曼滤波算法的抗野值问题,文献[9]提出了一种将新息序列加权的方法来消除野值影响。该方法认为当观测数据不包含野值时,滤波算法能够充分利用有效新息,对观测噪声进行在线估计;当观测数据出现野值时,能够克服其不利影响,或者能将其影响控制在某预先给定的范围内,以确保滤波估计值尽可能接近系统真实状态。
这里,为了更好地提高滤波精度,将这种新息加权的方法整合到该卡尔曼滤波算法中,得到一种新息序列加权卡尔曼滤波算法,如下式所示:

其中Ck为适当选取的门限值或常数序列,λk为KkDkKkT矩阵的最大特征值。τk服从自由度为m的χ2分布,m为观测数据Zk的维数,此处为1。若取χ2分布置信度为(1-α)×100%的上侧分位数为Cαm,α常取0.05或0.025,则Ck为

在工程问题的具体应用中,门限值Ck也可根据实际情况选取。
2.3 具体步骤综上所述,解决GPS卫星校准本地晶振频率源的误差修正问题步骤如下:
1)分析GPS信号中随机干扰和晶振累计误差分布,建立GPS校准晶振的频差信号数学模型。
2)根据频差信号数学模型推导出系统状态方程和观测方程,对系统状态和参数进行联合估计。
3)利用抗野值卡尔曼滤波算法,根据一系列观测值对含有各种噪声、野值的频差信号进行误差在线修正,得到高精度的频差信号值。
4)将修正后的频差信号值输入D/A转换模块转换为控制电压,实时调整晶振输出频率,实现系统高精度频率输出。
3 仿真验证 3.1 数值仿真下面进行数值仿真实验,验证上述新息序列加权卡尔曼滤波算法的有效性。其中系统方程如式(6)、式(7)所示,Rk=[1],Qk按照使滤波效果最优的原则由实验确定,本实验取0.000 05。输入状态X的初值为5.0×10-9 s,参数b初值为2×10-12,观测值Z在X上加以噪声和野值,如图 2所示。

|
| 图 2 随机观测值 |
用新息序列加权卡尔曼滤波算法进行处理,结果如图 3所示,其中虚线表示状态真值,实线表示滤波后的估计值。

|
| 图 3 滤波后的估计值 |
根据公式 ,分别计算滤波前后的均方误差(MSE),其中S表示均方误差,Xi为任意时刻值,
,分别计算滤波前后的均方误差(MSE),其中S表示均方误差,Xi为任意时刻值, 为数据均值,n为300。结果如表 1所示。
为数据均值,n为300。结果如表 1所示。
通过图 3可看出,经新息序列加权卡尔曼滤波算法处理后的数据更接近真实值。滤波后的均方误差明显小于滤波前的均方误差。本实验验证了新息序列加权卡尔曼滤波算法能够较好滤除数据中包含的随机噪声和较大野值。
3.2 实例验证在具体工程实践应用中,设定连续两次频差测量间隔为10 s,针对某GPS校准晶振频率源系统,在未进行滤波的情况下,采集了一组初始相对频差约为5.0×10-10,含有噪声干扰的频差信号数据[11],如图 4所示。

|
| 图 4 带有噪声干扰的频差信号(采样间隔10s) |
用状态和参数联合估计卡尔曼滤波算法处理带有噪声干扰的频差信号,结果如图 5所示。

|
| 图 5 应用卡尔曼滤波算法后的频差信号(采样间隔10s) |
利用新息序列加权卡尔曼滤波算法对原始测量数据进行处理,结果如图 6所示。

|
| 图 6 应用抗野值卡尔曼滤波算法后的频差信号(采样间隔10s) |
图 4表示系统直接测得未进行滤波的频率差信号波形图,可看出该频差信号的随机抖动很大,一般在±70×10-9以内,甚至还包含个别较大的野值。图 5是经过卡尔曼滤波后的频率差信号波形图,抖动已被减小到±2×10-9以内。但图 5中曲线在1 500~3 500 s之间有明显波动,是由于频差信号存在野值。这说明采用状态与参数联合估计的卡尔曼滤波算法虽具有一定的抗野值和消除噪声的能力,但是其估计值还是有明显的偏离[12, 13, 14]。图 6是应用了新息序列加权卡尔曼滤波算法后的频差信号波形图,可看出野值被有效抑制,滤波输出逐渐趋向于相对频差的真实值,并在真值即0.4×10-9上下波动。说明新息序列加权卡尔曼滤波算法对噪声的滤除效果明显优于未改进的卡尔曼滤波算法。
用该经过新息序列加权卡尔曼滤波算法处理后的频差信号,实时调整晶振的振荡频率,能保证GPS校频系统的输出频率准确度优于1.0×10-12。
4 结束语本文研究了GPS信号校准晶振信号频率源误差在线修正的方法。建立了GPS信号校准晶振信号的频差数学模型,利用状态和参数联合估计的卡尔曼滤波算法对GPS秒信号抖动、晶振累计误差等噪声进行实时在线修正;针对频差信号中存在野值的问题,对卡尔曼滤波算法进行了改进,通过新息序列加权来抑制新息方差的变化,进而消除随机噪声和野值的影响,并给出了数值仿真和实例验证。将该方法用于某GPS校频晶振频率源系统,能够满足高准确度频率输出的要求。
| [1] | 单庆晓,杨俊. 卫星驯服时钟系统的新进展[J]. 测试技术学报,2009,23(5):396-401. |
| [2] | 范文晶. 基于GPS信号锁定二级频标技术的研究与实现[D]. 西安:西安电子科技大学,2010. |
| [3] | 倪媛媛,胡永辉,何在民. 北斗卫星校准铷钟单元的设计与实现[J]. 测试技术学报,2011,15(2):56-59. |
| [4] | 党晓圆,单庆晓,肖昌炎,等. 基于GPS与北斗双模授时的压控晶振校频系统的研究与设计[J]. 计算机测量与控制,2009,17(11):2246-2248. |
| [5] | 曾祥君,尹项根,林干,等. 晶振信号同步GPS信号产生高准确度时钟的方法及实现[J]. 电力系统自动化,2003,27(8):49-53. |
| [6] | 曾祥君,尹项根,LI K K,等. GPS时钟在线监测与修正方法[J]. 中国电机工程学报,2002,22(12):41-46. |
| [7] | 李泽文,曾祥君,黄智伟,等. 基于高精度晶振的GPS秒时钟误差在线修正方法[J]. 电力系统自动化,2006,30(13):55-58. |
| [8] | 蒋陆萍,曾祥君,李泽文,等. 基于GPS实现电力系统高精度同步时钟[J]. 电网技术,2011,35(2):201-206. |
| [9] | 刘伟,赵伟,刘建业. 抗野值自适应Kalman滤波在无人机测风数据处理中的应用[J]. 弹箭与制导学报,2011,31(3):237-240. |
| [10] | 赵宏伟,廉保旺,冯娟. 基于Kalman滤波的授时测量系统研究[J]. 计算机测量与控制,2009,17(8):1517-1519. |
| [11] | 孙江涛. 基于GPS的1PPS的二级频标驯服技术[D]. 西安:西安电子科技大学,2010. |
| [12] | 郭芳. 用GPS秒信号锁定高频振荡器的方法研究[J]. 时间频率学报,2004,12(27):94-101. |
| [13] | DEERGHA R K, SWAMY M N S, EIPLOTKIN G P S. Navigation with Increased Immunity to Modeling Errors[J].IEEE Transactions on Aerospace and Electronic Systems,2004,40(1):2-11. |
| [14] | MOSAVI M R. Use of Accurate GPS Timing based on Radial Basis Probabilistic Neural Network in Electric Systems[C]//International Conference on Electrical and Control Engineering,2010:2572-2575. |
 2016, Vol. 42
2016, Vol. 42



