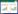文章信息
- 张志强, 张国胜, 刘艳芳, 王军威, 高素梅
- ZHANG Zhiqiang, ZHANG Guosheng, LIU Yanfang, WANG Junwei, GAO Sumei
- 断铅试验声发射信号处理与损伤源定位研究
- Research of acoustic emission signal processing and damage source location based on breaking lead test
- 中国测试, 2015, 41(8): 17-21
- CHINA MEASUREMENT & TEST, 2015, 41(8): 17-21
- http://dx.doi.org/10.11857/j.issn.1674-5124.2015.08.004
-
文章历史
- 收稿日期: 2014-09-21
- 收到修改稿日期: 2014-10-28
2. 天津职业大学, 天津 300410
Machinery, Tianjin 300409, China;
2. Tianjin Vocational Institute, Tianjin 300410, China
声发射是指材料因局部损伤导致能量的快速释放而产生瞬态弹性波现象[1, 2]。经过60多年的研究,声发射检测基础理论已经比较成熟,目前制约其广泛应用的主要障碍是声发射信号易被频率分布广泛的噪声掩埋,声发射信号特征提取是故障诊断的主要内容。在声发射检测前,为保证声发射传感器与被测试件的良好耦合,断铅试验是一种稳定、可靠、重复性高的验证方法,常用于模拟损伤源。参数分析法和波形分析法是声发射信号处理最常用的方法,主要用于描述声发射源特性以及评估材料损伤程度。声发射源定位也是声发射检测的重要内容。
成建国等[3]通过设计特征提取器来提取金属疲劳声发射特征信号,认为质心频率、计数、持续时间、上升时间、平均信号电平5个参数的特征最为显著,可用于识别现场环境下的声发射信号。马佳良等[4]通过建立四分类模型对罐底腐蚀声发射信号进行识别,将声发射特征参数和频域参数作为模型的输入参数,获得了较好的识别结果。李东生等[5]采用声发射技术监测斜拉索疲劳损伤演化过程,获得了整个损伤过程的声发射特征参数,基于声发射累积能量得出了多龄期斜拉索疲劳损伤演化规律。李国禄等[6]首次对等离子喷涂层接触疲劳损伤过程中的声发射特征参数进行了系统研究,结果表明声发射幅值、有效值、能量、计数和平均频率等对疲劳损伤过程具有实时性反馈的特点。Aljets D等[7]以大型平板状结构为对象研究了3个传感器呈三角布置的声发射源定位的新方法,结合信号传播速度和模态源定位算法进行了损伤源的准确定位。Li Q Y等[8]以断铅模拟岩石中的声发射源,定量研究了线定位和平面定位下声速对于定位误差的影响,结果表明声速严重影响平面定位精度,而且平面定位较线定位误差更大。Niri E D等[9]采用微型脉冲锤模拟声发射源,将非线性卡尔曼滤波算法用于评估声发射源的定位精度,结果表明定位精度较高。本文以断铅试验为例模拟材料的断裂损伤事件,进行了声发射特征参数和损伤源定位的试验研究,采用小波变换对声发射信号进行分解和重构,提取包含断铅的特征波形和频率。 1 声发射信号的采集
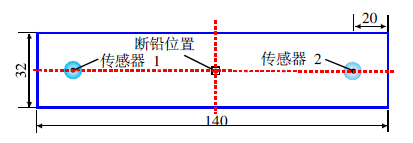
采用美国物理声学公司(PAC)生产的四通道声发射系统采集断铅声发射信号,该系统主要由Nano-30型压电传感器、前置放大器、PCI-2数据采集卡以及AEWin声发射信号记录和分析软件组成。Nano30型传感器靠压电效应,将材料局部损伤以能量形式释放的弹性波传化为电信号。设定前置放大器放大额度为40 dB。门槛值设定为45 dB,带通滤波区间设定为1 kHz~1 MHz,信号采样频率设为1 Mb/s。采用直径为0.5 mm的HB铅芯在32 mm×140 mm的矩形试件表面进行断铅试验,铅芯伸长量为2.5 mm,每次断铅时保证铅芯与试件表面夹角为30°。传感器1和传感器2分别置于距离试件端面20mm处,并采用磁性夹具固定。传感器和试件之间涂有真空脂,目的是减少声发射信号在传感器和试件界面处过度散射和衰减。断铅位置选为试件中心,连续进行14次断铅试验来模拟14次加载过程,时间间隔为4 s,传感器布置方式和断铅位置如图 1所示。传感器1采集的14次断铅声发射信号幅值分布图如图 2所示,可以看出声发射信号幅值均达90 dB,14次断铅声发射信号幅值平均值为98 dB。传感器2采集的14次断铅声发射信号幅值分布与传感器1极为相近,幅值平均值为98.8 dB。两个传感器采集的每次断铅声发射波形也极为类似,为典型的高衰减突发性声发射信号。图 3为传感器1采集的第6次断铅声发射波形图,可以看出,开始采集到的幅值为3 mV左右的信号,为铅芯和试件表面接触时由于微摩擦产生的声发射信号,最先产生的幅值为9 mV以上的信号才是铅芯断裂激发的声发射信号;之后信号逐渐衰减,衰减趋势如图中灰色线所示,开始时信号衰减速度较慢,然后快速衰减至4 mV以下,直至被环境噪音信号掩埋。
 |
| 图 1 断铅试验示意图(单位:mm) |
 |
| 图 2 14次断铅声发射幅值 |
 |
| 图 3 断铅声发射信号波形 |
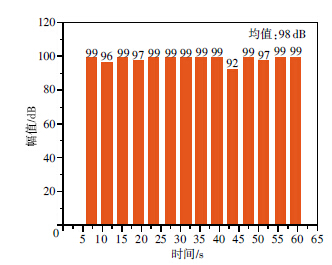
声发射计数、能量和有效值是分析材料损伤程度的重要特征参数。幅值是指一次撞击中声发射振幅的最大值,其与损伤程度有直接关系。振铃计数是指一次撞击中信号越过门槛值的个数,反应信号的强度和频度,对裂纹的扩展比较敏感,可用于波源类型鉴别。能量是指一次撞击中声发射幅值对持续时间的积分值,反映事件的相对能量或强度,可以有效地分析复杂背景噪声下的声发射信号,较好地去除白噪声干扰,也可用于复杂声发射信号活动性评价。均方根值(RMS)是一次撞击中声发射振幅平方的平均值的平方根,其对门槛值、工作频率和传播特性不甚敏感,可以很好地反映材料的损伤程度。由于传感器1和传感器2采集到的14次断铅声发射特征参数值和分布基本相同,所以仅以传感器1采集到的断铅声发射信号为例进行说明。图 4和图 5分别为14次断铅声发射计数柱状分布图和累计计数梯形分布图,可以看出断铅声发射计数主要分布在627~1 955范围之内,计数的高低反应了断铅释放能量的高低,也侧面反应了铅芯质量的好坏和同一根铅芯不同位置的均匀化程度,通过累积计数分布图可以更加直观地看出前后两次断铅事件计数的梯度值,累计分析在材料连续累积损伤程度分析应用中尤为重要。图 6和图 7分别为14次断铅声发射能量和有效值柱状分布图,可以看出断铅声发射能量主要分布在6 412~39 054范围内,有效值主要分布在0.046 2~0.513 2范围内;14次断铅声发射能量和有效值与计数的分布趋势和相对变化梯度基本一致,第10次断铅声发射计数、能量和有效值额度最小,铅芯脆断释放的能量最低,第5次断铅声发射计数、能量和有效值额度最大,铅芯脆断释放的能量最高。而通过图 2可以看出,每次断铅声发射幅值变化很小,有10次断铅声发射幅值同为99 dB;因此,依据每次断铅释放的声发射信号幅值并不能较好的判定断铅事件能量的高低。
 |
| 图 4 14次断铅声发射计数 |
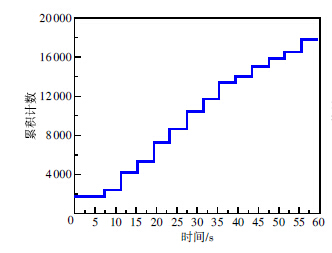 |
| 图 5 14次断铅声发射累积计数 |
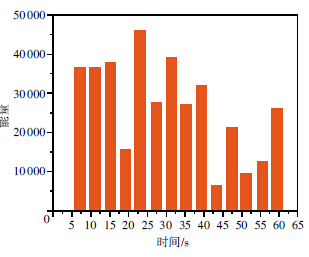 |
| 图 6 14次断铅声发射能量 |
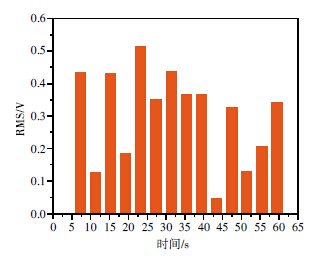 |
| 图 7 14次断铅声发射能量有效值柱状分布 |
声发射信号本身属于典型的非平稳信号,包含故障信息的特征信号往往被噪声所干扰。小波变换具有良好的时频局部特性,是信号奇异性检测的有力工具[10, 11]。通过小波变换对断铅产生的非平稳突发声发射信号在不同尺度上进行分解和重构,以期实现对其全频带上多个层次的划分,由粗及细地对信号进行逐步观察和分析,提取包含断铅特征的波形和频率。
小波函数的确切定义为:设φ(t)∈L2(R)为平方可积函数,若其傅里叶变换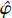 (ω)满足条件:
(ω)满足条件:
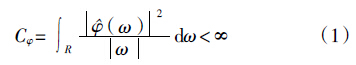
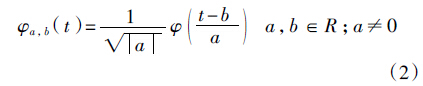
b——平移因子,称为φa,b(t)依赖与参数a,b的小波基函数。
由于a和b是连续变化的参数,因此称φa,b(t)为连续小波基。将任意L2(R)空间中的函数f(t)在小波基下展开,称其为函数f(t)的连续小波变换,其表达式为
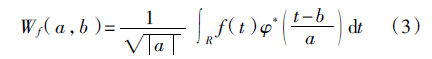
其重构公式(逆变换)为
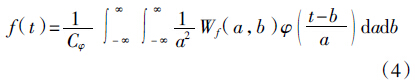
在实际运用中,尤其是在计算机上实现,连续小波必须加以离散化。通常,连续的尺度因子a和平移因子b的离散化公式分别取作:a=aj0,b=kaj0b0,j∈Z,其中a0,b0为扩展步长,对应的离散小波函数基φj,k(t)为
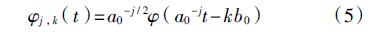
函数f(t)离散小波变换表达式为
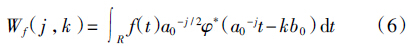
离散小波变换的重构公式(逆变换)为
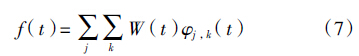
采用dB10基本小波对断铅声发射信号进行4层小波分解和重构。s为原始信号,d代表高频信息,a代表低频信息。d1,d2,d3,d4和a4分别表示第1,2,3,4层细节信号,d1层重构信号的频率范围为250~500 kHz,d2层重构信号的频率范围为125~250 kHz,d3层重构信号的频率范围为62.5~125 kHz,d4层重构信号的频率范围为31.25~62.5 kHz,a4层重构信号的频率范围为0~31.25 kHz。对传感器1采集的第6次断铅声发射信号进行4层小波分解和重构,各层波形和频率分别如图 8和9所示。从图 9中s层频率谱中可以看出原始信号的频率主要分布在120~200 kHz范围之内,其中存在130,150,195 kHz 3个比较集中的频率段,该原始断铅信号的全局功率谱包含断铅声发射信号、接触摩擦信号以及噪音等频率成分,并不能获得较为单一的断铅声发射信号频率特征分布。图 8中d1层信号波形幅值不足4 mV,频率主要分布在225~450 kHz范围之内,很有能是铅芯断裂前与试件接触摩擦产生的高频声发射信号。图 8中d2层信号波形幅值高达10 mV,该层主要是铅芯断裂的声发射信号,频率主要分布在125~200 kHz范围之内,其中存在125,130,150,195 kHz 4个比较集中的频率段。图 8中d3层信号波形幅值高达8 mV,该层信号仍然以铅芯断裂的声发射信号为主,频率主要分布在100~130 kHz范围之内,其中存在127,130 kHz两个比较集中的频率段。图 8中d4和a4层信号波形幅值都不足2 mV,频率主要分布在20~65 kHz范围之内,主要是低频噪音干扰信号。综上所述,采集到的断铅声发射原始信号是由断铅信号、接触摩擦信号和噪音等信号叠加的综合结果,属于能量较弱的非平稳信号。采用小波变换将原始的声发射信号分解到不同的频率段并进行重构,在不同的频率段将时域波形和频率分布对应分析,这种时频分析的方法可以将高频和低频干扰信号剔除,准确提取断铅特征信息。
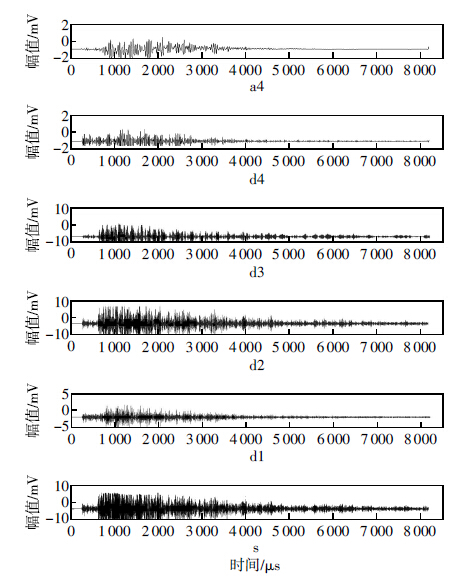 |
| 图 8 小波变换声发射波形 |
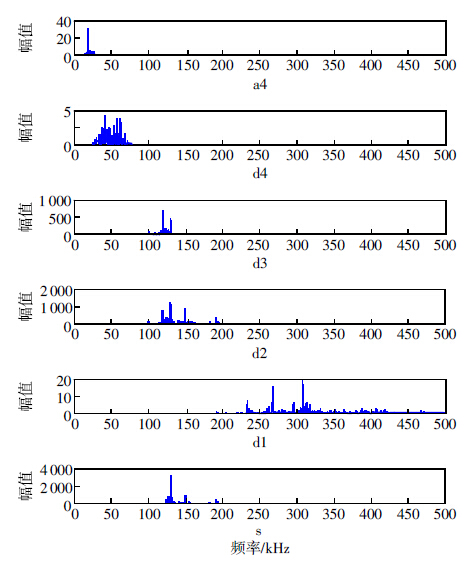 |
| 图 9 小波变换声发射频率谱 |
声发射源定位是声发射检测的主要目的之一,需由多通道声发射仪器来实现。时差定位是声发射源定位最基本的方法,它是根据声发射信号到达不同通道传感器的时间差、波速和传感器间距来确定声发射源位置的方法。本研究的断铅试件为长条矩形试件,因此可采用时差线定位法对断铅位置进行定位,定位原理如图 10所示。如在传感器1和传感器2之间有一个声发射源产生声发射信号,到达传感器1的时间为t1,到达传感器2的时间为t2,该信号到达两个探头之间的时差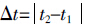 ,以D表示两传感器间的距离,以V表示声波在试样中的传播速度,则声发射源距传感器1的距离d可由下式得出:
,以D表示两传感器间的距离,以V表示声波在试样中的传播速度,则声发射源距传感器1的距离d可由下式得出:
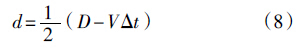
由式(8)可知,当Δt=0时,声发射源位于两传感器中间;当Δt=D/V时,声发射源位于传感器1处;当Δt=-D/V时,声发射源位于传感器2处。断铅激发声发射信号的位置选为试件中心,声波在试样中的传播速度设定为5 500 m/s。定位结果如图 11所示,可以看出定位数据点基本落在试件中心位置附近,偏差不超过10 mm。
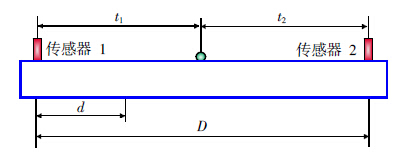 |
| 图 10 时差线定位原理图 |
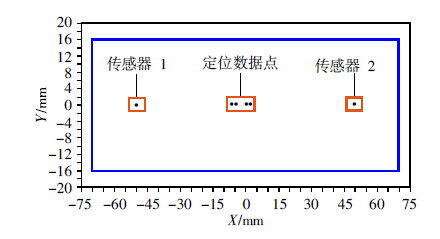 |
| 图 11 断铅定位图 |
1)声发射计数、能量和有效值对于材料损伤程度具有较高的灵敏度,仅依据声发射幅值的高低并不能判断铅芯断裂释放的声发射信号能量的高低。
2)原始声发射信号是断铅信号、接触摩擦信号和噪音等信号叠加的综合结果。采用小波变换将原始声发射信号分解到不同的频率段并进行重构,将时域波形和频率分布对应分析,实现了将高频接触摩擦信号和低频噪音信号剔除并准确提取断铅特征信息的目的。
3)采用多通道声发射系统对断铅位置进行定位是完全可行的,时差线定位偏差不超过10 mm。
| [1] | Lindley T C, Palmer I G, Richards C E. Acoustic emission monitoring of fatigue crack growth[J]. Materials Science and Engineering,1978,32(1):1-15. |
| [2] | 杨明纬. 声发射检测[M]. 北京:机械工业出版社,2005:2-4. |
| [3] | 成建国,毛汉领,黄振峰,等. 金属材料声发射信号特征提取方法[J]. 声学技术,2008,27(3):309-314. |
| [4] | 马佳良,于洋. 基于相关向量机模型的腐蚀声发射信号识别[J]. 环境技术,2014(1):23-26. |
| [5] | 李冬生,胡倩,李惠. 多龄期桥梁斜拉索疲劳损伤演化声发射监测技术研究[J]. 振动与冲击,2012,31(4):67-71. |
| [6] | 李国禄,张志强,王海斗,等. 涂层疲劳损伤声发射特征参数及损伤机理[J]. 材料工程,2013(6):45-49. |
| [7] | Aljets D, Chong A, Wilcox S, et al. Acoustic emission source location on large plate-like structures using a local triangular sensor array[J]. Mechanical Systems and Signal Processing,2012(30):91-102. |
| [8] | Li Q Y, Dong L J, Li X B, et al. Effects of sonic speed on location accuracy of acoustic emission source in rocks[J]. Transactions of Nonferrous Metals Society of China,2011,21(12):2719-2726. |
| [9] | Niri E D, Farhidzadeh A, Salamone S. Nonlinear kalman filtering for acoustic emission source localization in anisotropic panels[J]. Ultrasonics,2014,54(2):486-501. |
| [10] | 韩磊,程礼,苗学问. 基于小波分析的航空发动机轴承故障诊断[J]. 轴承,2008(10):30-34. |
| [11] | Zhu K P, Wong Y S, Hong G S. Wavelet analysis of sensor signals for tool condition monitoring: A review and some new results[J]. International Journal of Machine Tools & Manufacture,2009,49(7-8):537-553. |
 2015, Vol. 41
2015, Vol. 41