文章信息
- 任寰弋, 童玲
- REN Huan-yi, TONG Ling
- 一种减小ADI-FDTD误差的方法
- A method to reduce error of ADI-FDTD
- 中国测试, 2007, 33(4): 102-104128
- CHINA MEASUREMENT & TEST, 2007, 33(4): 102-104128
- http://dx.doi.org/2007-04/20070430.htm
-
文章历史
- 收稿日期: 2006-12-07
- 收到修改稿日期: 2007-02-03
时域有限差分法( Finite - Difference Time -Domain- FDTD) 以Yee 氏立体网格作为电磁场离散单元,将麦克斯韦方程转化为差分方程,能够方便有效的结合计算机技术处理复杂的电磁场问题[1],目前已经在电磁学的各个领域中得到了广泛的应用。然而其计算效率却受Courant- Friedrich- Levy( CFL) 稳定条件的限制,尤其体现在高Q 值结构和场变化非常迅速的结构的地方。为了克服这个限制,人们提出了无条件稳定的基于交变隐式差分方向方法的时域有限差分法———ADI - FDTD 方法 和 Crank - Nicolson( CN) FDTD 方法[2]-[5]。由于它们的无条件稳定性,两种方法都引起了不少关注。在研究中,人们发现,虽然这两种方法计算效率提高了不少,但当时间步长取得较大的话,ADI- FDTD 方法也会伴随着较大的误差。另一方面,CN- FDTD 方法虽然在大时间步长下要精确一些,但却是以更多的计算时间作为代价换来的。
针对ADI- FDTD 方法存在较大的数值色散误差的问题,国内外许多专家学者都进行了研究。比较常见的有两种方案: 一种方法是采用高阶差分。普通的ADI- FDTD 方法在空间上取的是二阶近似,为了进一步提高计算精度,可将Maxwell 方程的空间近似式取四阶有限差分。文献[11]中已详细论证了采用这种高阶差分迭代式仍然是无条件稳定的,而数值色散比二阶差分算法显著减小。不过这种方法的缺点是增加了计算的复杂性。另一种方法是在运算空间增加各向异性介质控制数值色散,减小误差。实际计算表明,采用该方法并选取适当的介电常数,即可改善ADI- FDTD 相速特性,很大程度上消除其色散现象。但其存在着有待进一步研究的问题: 如何处理在消除某段频率范围色散误差时出现的低频部分误差增加的情况,以及怎样在计算空间中自由地控制更宽频带范围的相速,令其同时接近相速理想值。
本文有别于以上两种方法,提出了另一种基于CN- FDTD公式的ADI- FDTD方法,它能提高计算的精度,却具有和常规ADI- FDTD同样的计算效率。虽然提高之后的精度仍无法达到CN- FDTD的水平,但也足够满足大多数大时间步长的仿真而不用增加计算开销。
2 理论分析2.1 公式变换首先,将Maxwell 方程组表示为矩阵的形式:
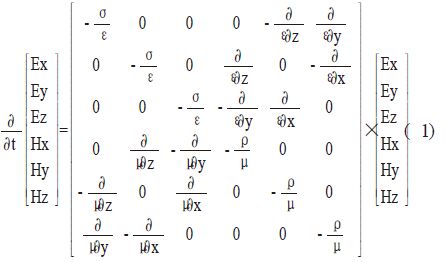
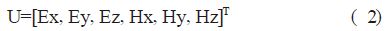
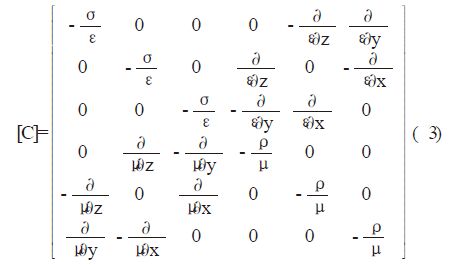



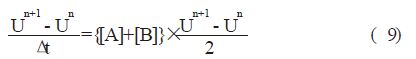
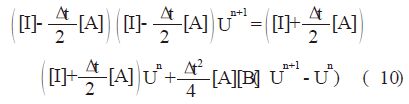
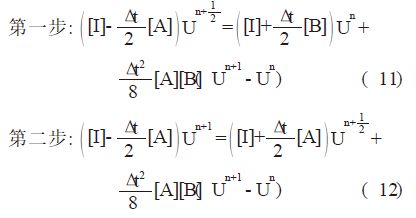
上面的两个方程都是隐式方程,一般是采用迭代的方法来求解。本文提出了另两种方法,这两种方法在方程的右边是显式的,不需要在每一个时间步上进行迭代。
方法一: 对于上面( 10) 式中右边$\frac{\Delta {{t}^{2}}}{4}$[A][B]( Un+1- Un) 中的U,我们用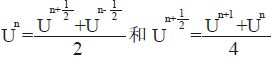
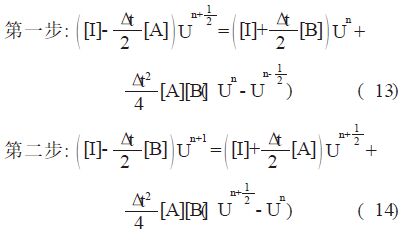
方法二: 对于上面( 10) 式中右边$\frac{\Delta {{t}^{2}}}{4}$[A][B]( Un+1- Un)中的U,我们用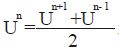 来近似,可得到以下两个步骤:
来近似,可得到以下两个步骤:
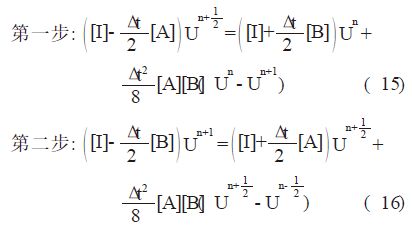
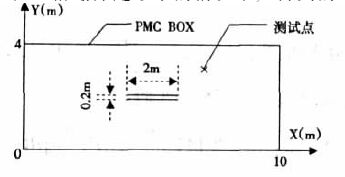
出于完整性,上文分析了三维包含了电流源和有耗介质情况下的公式。为了简单的说明问题,这里考虑二维不包含电流源并且是无耗介质的情况: 如图 1,在四周都是PMC 包围的自由空间中,有两个平行导电板,y 方向相距0.2m,板宽均为2m,平行板位于自由空间的中部,被PMC 包围的自由空间的大小为x 方向10m,y 方向4m。采用750kHz 正弦源,在x=7m,y=3.1m 处,根据不同的CFL 参数( 用s 来表示,$s=\frac{c\bullet \Delta {{t}^{{}}}}{\Delta }$,Δ为网格宽度) 考察Ey。这里定义Ey 的相对误差为:$\frac{E_{y}^{m}-E_{y}^{r}}{E_{y}^{r}}$,其中Eym 表示在考察点处由上面公式得到的Ey 值; Eyr 表示在考察点由普通FDTD方法,在网格划分足够小的情况下,得到的Ey 的值。
|
| 图 1 被PMC风暴的自由空间中的平行导电金属板 |
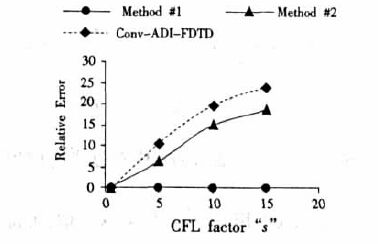
图 2 表示出了关于不同CFL 参数“s”的上述两种方法的相对误差,为了便于比较,图中还画出了传统ADI- FDTD 关于“s”的相对误差。我们可以看出,当“s”小于0.5 的时候,三种方法的相对误差都很小,和FDTD 差不多。但是当“s”增大的时候,传统ADIFDTD和第二种方法的相对误差都开始增大,但是第二种方法明显要小于传统ADI- FDTD,而第一种方法的相对误差却仍然和FDTD 一样,没有增大。
|
| 图 2 关于CFL参数的“s的相对误差” |
另外,从以上两种方法和传统ADI- FDTD 的表达式可以看出,他们的计算时间和内存占用应该是基本一致的,而本文提出的两种方法,尤其是第一种方法计算的误差明显小于传统ADI- FDTD,这无疑增加了ADI- FDTD 方法的计算精度,扩展了其应用的范围。
4 结论为保证计算的准确高效性,ADI- FDTD 必须在原有的无条件稳定、计算时间短等优点的基础之上进行发展,尽量减少内存使用量,简化计算的复杂性,并控制其数值色散。在本文中,提出了两个减小ADI- FDTD 误差的计算方法。数值计算结果证明了它们在保持和传统ADI- FDTD 方法相同计算效率的同时,达到了与CN- FDTD 方法相似的计算精度。尤其是文中的第一种方法,在大时间步长时,仍然保持与传统FDTD 相同的计算精度,大大提高了ADI- FDTD 方法的实用意义。本文提出的方法奠定了进一步研究ADI- FDTD 误差的基础,对为何这两种方法减小了误差,还有待进一步的理论研究。
| [1] | 王秉中.计算电磁学[M].北京:科学出版社, 2005. |
| [2] | Namiki T. A new FDTD algorithm based on alternating-direction implicit method[J]. IEEE Trans. Microw., 1999, 47(10):2003-2007. |
| [3] | Zheng F, Chen Z and Zhang J. Toward the development of a three-dimensional unconditionally stable finitedifference time-domain method[J]. IEEE Trans. Microw. Theory Tech., 2000, 48(9):1550-1558. |
| [4] | Garcia S G, Lee T W and Hagness S C. On the accuracy of the ADI-FDTD method[J]. IEEE Antennas Wireless Propag. Lett., 2002, 1:31-34. |
| [5] | Sun G and Trueman C W. Approximate crank-nicolson schemes for the 2-D finite difference time domain method for TEz waves[J]. IEEE Trans. Antennas Propag., 2004, 52(11):2963-2972. |
| [6] | Wang S, Teixeira F L and Chen J. An iterative ADIFDTD with reduced splitting error[J]. IEEE Microw. Compon. Lett., 2005, 15(2):92-94. |
| [7] | Namiki T. 3-D ADI-FDTD method unconditionally stable time-domain algorithm for solving full vector Maxwells equations[J]. IEEE Trans.Microwave Theory and Techniques, 2000, 48(10):1743-1748. |
| [8] | Namiki T.A new FDTD algorithm based on alternatingdirection implicit method[J].IEEE Trans. Microwave Theory and Techniques, 1999, 47(10):2003-2007. |
| [9] | Kondylis G D, Flaviis F D,Pottie G J and Itoh T. A memory-efficient formulation of the finite-difference time-domain method for the solution of Maxwell equation[J]. IEEE Trans. Microwave Theory and Techniques, 2001, 49(7):1310-1320. |
| [10] | Chen Zhi-zhang, Iftibar Abmed. A hybrid ADI-FDTD scheme and its comparisons with the FDTD method[S]. IEEE Antennas and Propagation Society, AP-S International Symposium (Digest), 2003, 4:360-363. |
| [11] | Zheng Feng-hua, Chen Zhi-zhang, and Zhang Jia-zong. Development of three-dimensional unconditionally stable finite-difference time-domain methods[S]. IEEE MTT-S International Microwave Symposium Digest, 2000, 2:1117-1120. |
 2007, Vol. 33
2007, Vol. 33